Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

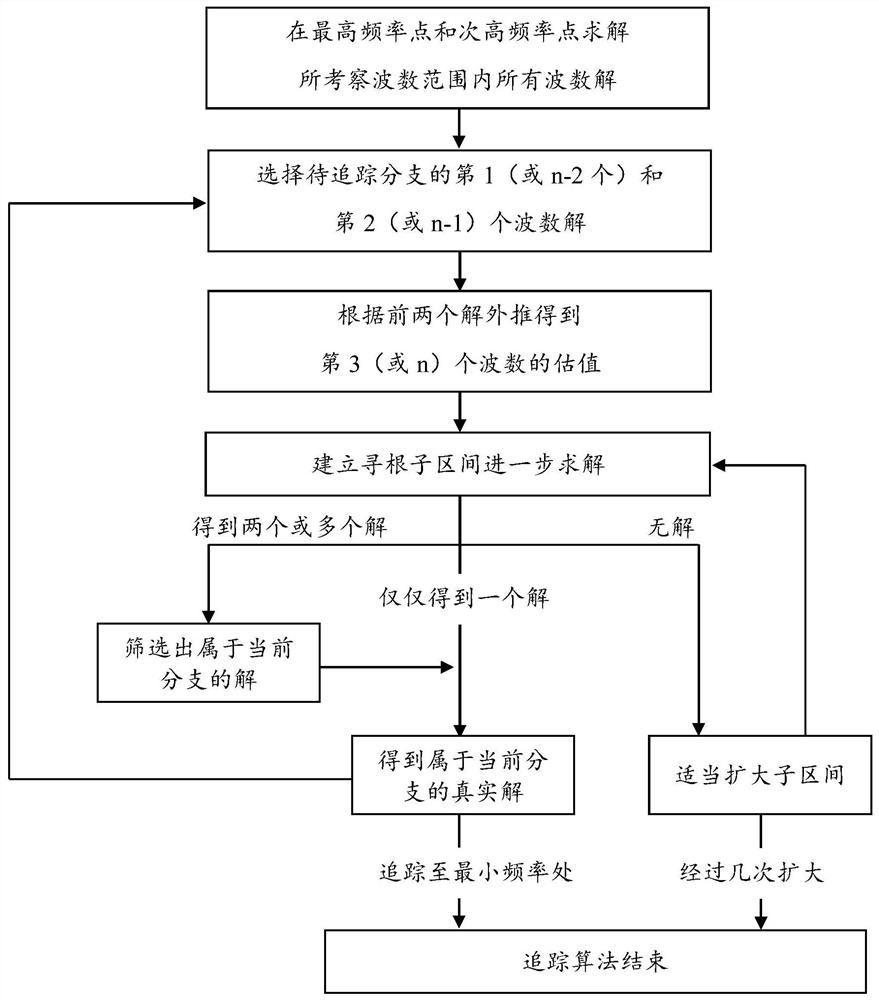
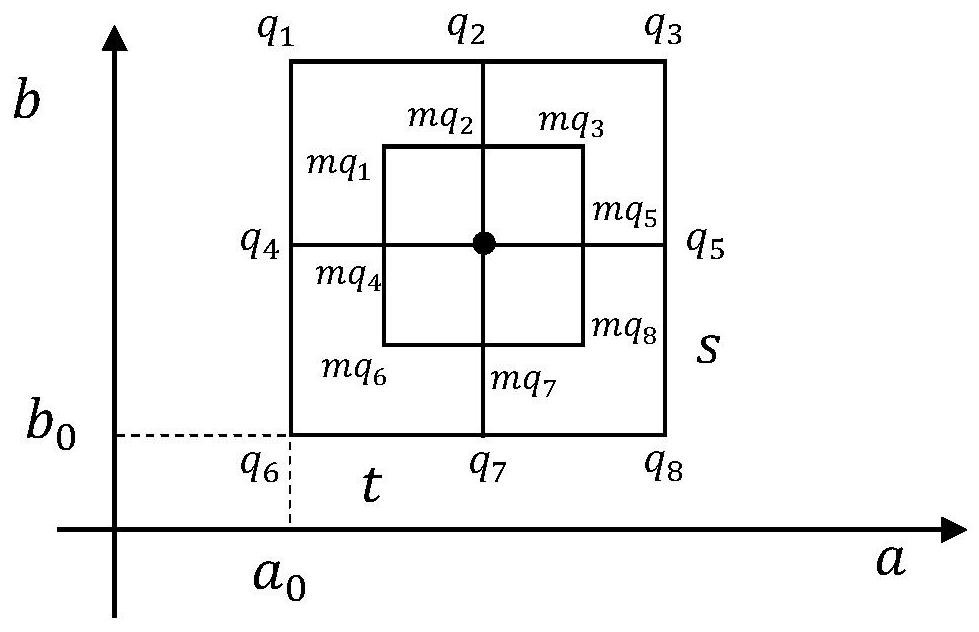
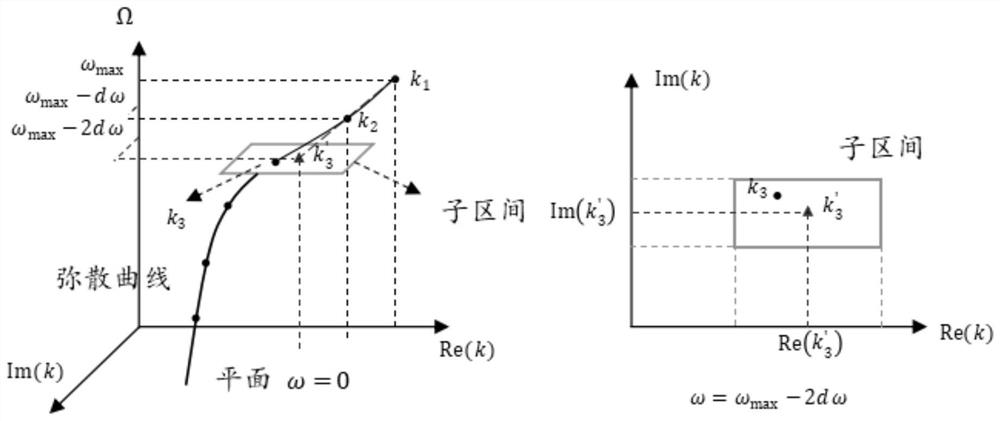
Numerical method for quickly drawing dispersion curve in complex wave number domain in waveguide structure

A technology of dispersion curves and numerical methods, applied in the field of drawing dispersion curves in the complex wavenumber domain, can solve problems such as large calculation time, achieve the effect of optimizing data structure and improving solution efficiency

Pending Publication Date: 2020-12-11
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The purpose of the present invention is to provide a numerical method for quickly drawing the dispersion curve in the waveguide structure, aiming to solve the problem that a large amount of calculation time must be spent when the traditional method guarantees the calculation accuracy

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Numerical method for quickly drawing dispersion curve in complex wave number domain in waveguide structure
  • Numerical method for quickly drawing dispersion curve in complex wave number domain in waveguide structure
  • Numerical method for quickly drawing dispersion curve in complex wave number domain in waveguide structure

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0087] The spectrum of the Rayleigh-Lamb wave, the dispersion equation of its longitudinal mode is:

[0088]

[0089] Ω and Z are frequency and wavenumber, respectively.

[0090]

[0091] where C T，L is the bulk wave velocity of the material, η T，L are the attenuation coefficients per unit wavelength, respectively.

[0092] Considering the case of viscoelasticity, the parameters are set as follows:

[0093]

[0094] Solved with the modal tracking separation method of the present invention to obtain Figure 5 .

[0095] Consider the case of pure elasticity, that is, η T = η L = 0, obtained by using the mode tracking separation method of the present invention Figure 6 .

[0096] The bending mode dispersion equation is:

[0097]

[0098] The results obtained by solving the viscoelastic structure with the mode tracking separation method of the present invention are as follows: Figure 7 , the purely elastic mode separation results in Figure 8 .

Embodiment 2

[0100] Considering the propagation of Lamb waves in an isotropic double-layer plate, the dispersion equation can be expressed as:

[0101] |A(ω,k,λ n ,μ n , h n )|=0 (n=1,2) (5)

[0102] Matrix A is the coefficient determinant, where the material parameter is λ n and μ n , geometric parameter h n , the frequency is ω, and the wavenumber is k. The parameters are set as follows

[0103]

[0104] First apply η in layer 1 T = η L = 0.01 viscosity coefficient, the result obtained by using the mode tracking separation method of the present invention is as follows Figure 9 shown.

[0105] First use the mode tracking separation method of the present invention to solve the results in the pure elastic structure, such as Figure 10 shown.

[0106] It can be seen from the figure that the calculated modal branches of the pure elastic structure and the viscoelastic structure do not completely match, and the method of mode tracking separation is only effective for some low-or...

Embodiment 3

[0109] Investigating the wave propagation in the infinite piezoelectric plate, the dispersion equation of the symmetrical mode is:

[0110]

[0111] Ω and Z represent frequency and wavenumber, respectively. Without distinguishing between modes, use the dispersion curve drawing method of the present invention to solve Figure 12 (k=0.48).

[0112] The dispersion equation of its antisymmetric mode is:

[0113]

[0114] Ω and Z represent frequency and wavenumber, respectively. Without distinguishing between modes, use the dispersion curve drawing method of the present invention to solve Figure 13 (k=0.48). The initial wave numbers for tracing roots include pure real numbers, pure imaginary numbers and complex numbers.

[0115] The present invention describes a method for drawing the dispersion equation in the complex wavenumber domain by means of single-branch tracing and root-finding, and based on this, it proposes a method that can simultaneously separate modes and ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a numerical method for quickly solving a dispersion curve in an acoustic wave sensor. The numerical method utilizes a method of sequentially tracking and drawing single dispersion curve branches to form a complete space dispersion curve. The method comprises the following steps: establishing a subinterval for solving the next wave number by utilizing the first two wave numbers of a current tracking branch; and employing a screening method when multiple solutions appear in a sub-interval in the tracking process. According to the method, the problem that a large amount ofoperation time is consumed due to the fact that the solving accuracy and completeness are improved when a space dispersion curve is solved through a conventional method is effectively solved, separated storage of each piece of modal data can be achieved to a certain extent, and a data storage structure is optimized. The method can be suitable for drawing and solving spatial dispersion curves in various types of waveguide structures, and brings great convenience to propagation analysis and subsequent application of waves in various sensor models.

Description

technical field [0001] The invention belongs to the technical field of acoustic wave sensors, in particular to a method for drawing dispersion curves in the complex wave number domain. Background technique [0002] The research on the theory and application of ultrasonic guided waves is widely used in the field of sensor technology and non-destructive testing. In order to better apply the ultrasonic guided wave, it is necessary to study the propagation characteristics of the guided wave, that is, to analyze the frequency, wave number, phase velocity and group velocity of the ultrasonic guided wave in the waveguide. Among them, when a wave propagates in a specific structure, its dispersion relationship (that is, the relationship between wave number and frequency) is certain. By extrapolating and solving the dispersion equation, the displacement field distribution can be obtained. Therefore, theoretically calculating the dispersion relationship of waves propagating in the wa...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/11
CPCG06F17/11
Inventor 王彬焦帅笪益辉钱征华
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com