Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Intrinsic decomposition method of hyperspectral image based on digital surface model

A technology of digital surface model and hyperspectral image, applied in the field of hyperspectral image eigendecomposition, can solve the problem of low eigendecomposition accuracy of hyperspectral image, achieve the effect of eliminating spectral information degradation and improving accuracy

Active Publication Date: 2022-03-08
HARBIN INST OF TECH
View PDF9 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to solve the problem of low precision of the existing hyperspectral image eigendecomposition, and to provide a hyperspectral image eigendecomposition method based on digital surface model assistance

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Intrinsic decomposition method of hyperspectral image based on digital surface model
  • Intrinsic decomposition method of hyperspectral image based on digital surface model
  • Intrinsic decomposition method of hyperspectral image based on digital surface model

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

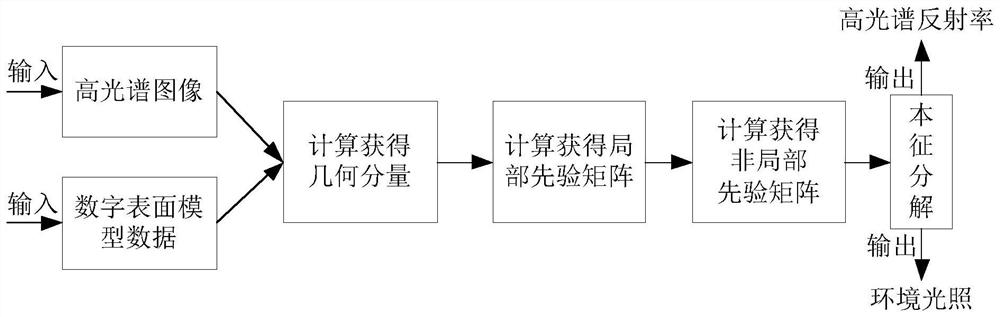
[0061] Specific implementation mode one: the following combination figure 1 Illustrate this embodiment, the hyperspectral image eigendecomposition method based on digital surface model assistance described in this embodiment, it comprises:

[0062] S1. Input hyperspectral images and digital surface model data, and calculate geometric components;

[0063] S2. Calculate and obtain a local prior matrix;

[0064] S3. Calculate and obtain a non-local prior matrix;

[0065] S4. Perform eigendecomposition according to the geometric component, local prior matrix and non-local prior matrix, and output hyperspectral reflectance and ambient light.

specific Embodiment approach 2

[0066] Specific implementation mode 2: This implementation mode further explains the implementation mode 1. The specific method for calculating and obtaining the geometric component described in S1 includes:

[0067] input hyperspectral image

[0068] Input digital surface model elevation data

[0069] Among them, h k =[h k (λ 1 ), h k (λ 2 ),…,h k (λ d )] T ,k=1,2,...,u represents the spectral feature of each pixel, k=1,2,...,u represents the index of each pixel, λ represents the wavelength, d represents the number of bands, u represents the height The number of spectral image pixels, z 1 ,z 2 ,…,z u Indicates the elevation corresponding to each pixel, represents the domain;

[0070] Calculate the normal of each pixel and obtain the normal feature:

[0071] in, Represents the projection of the normal on the x, y, and z space coordinate axes;

[0072] Calculate the geometric component J: J=[J 1 ,J 2 ,...,J u ] ú ;

[0073] in,

[0074]

[0075]...

specific Embodiment approach 3

[0078] Specific implementation mode three: this implementation mode further explains implementation mode two, and the specific method for calculating and obtaining the local prior matrix described in S2 includes:

[0079] Traverse the index k=1,2,...,u of each pixel and build a dictionary D k =[h 1 ,..., h k-1 ,h k+1 ,..., h u ,I d ];

[0080] Among them, I d Represents a d-dimensional identity matrix;

[0081] Calculate h according to the following formula k in dictionary D k The sparse representation coefficient α in :

[0082] min α ‖α‖ 1 subject to h k =D k α;

[0083] Each element W of the local prior matrix W kj Obtained by the following assignment:

[0084]

[0085] W kj Indicates the element of row k and column j of W;

[0086] alpha j Indicates the sparse representation coefficient for column j, α j-1 Indicates the sparse representation coefficients for the j-1th column.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A hyperspectral image eigendecomposition method assisted by a digital surface model belongs to the technical field of hyperspectral image fusion processing. The invention aims to solve the problem of low eigendecomposition precision of existing hyperspectral images. It includes: input hyperspectral image and digital surface model data, calculate and obtain geometric components; calculate and obtain local prior matrix; calculate and obtain non-local prior matrix; perform intrinsic Decomposed, output hyperspectral reflectance and ambient lighting. The invention is used for intrinsic decomposition of hyperspectral images.

Description

technical field [0001] The invention relates to a hyperspectral image intrinsic decomposition method, which belongs to the technical field of hyperspectral image fusion processing. Background technique [0002] Hyperspectral images have rich spectral information, but the high-dimensional spectral space also results in highly redundant information, which is not conducive to the processing and interpretation of information. In order to better mine information, various feature extraction methods have been designed, but these information extraction methods have essential defects. When the imaging conditions such as ambient light change, the spectrum obtained by imaging will also change accordingly, which makes the obtained spectrum have high uncertainty. This uncertainty is reflected in the extracted features, which will make the information expressed by the features Unreliable. In order to solve this problem, it is of great significance to study the eigendecomposition method ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06V10/77G06V10/772G06K9/62
CPCG06F18/2136G06F18/28
Inventor 谷延锋金旭东
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com