Point cloud classification method for LiDAR full waveform control decomposition driving
A waveform decomposition and full waveform technology, applied in radio wave measurement systems, instruments, etc., can solve the problems of small number of echo samples, limited accuracy of ground object classification, waveform distortion, etc., and achieve accurate waveform decomposition and extraction, accurate and efficient classification. Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0098] The following is a further description of the technical solution of the LiDAR full-waveform control decomposition-driven point cloud classification method provided by the application in conjunction with the accompanying drawings, so that those skilled in the art can better understand the application and implement it.
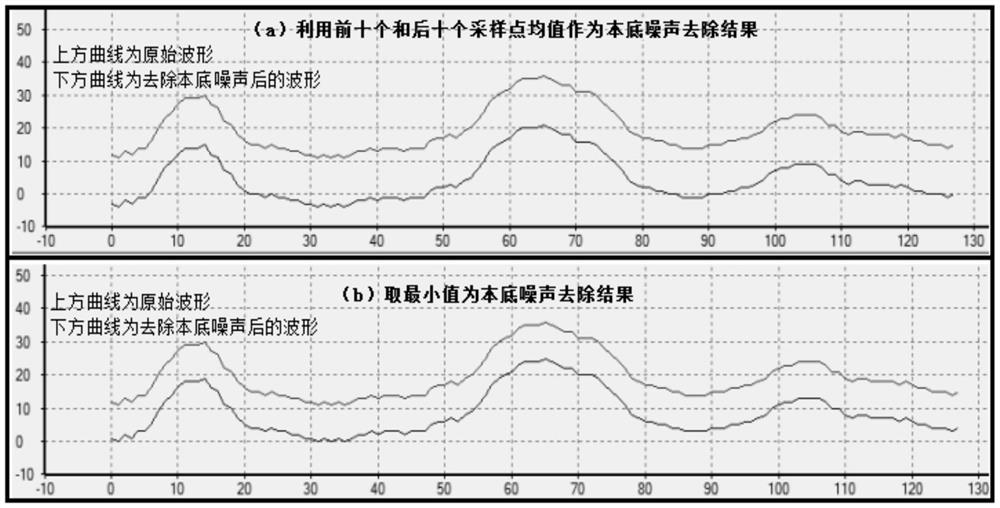
[0099] Traditional discrete airborne LiDAR usually only records the first echo and the last echo reflected by ground objects, while the multi-echo system records up to 4 to 5 echoes. Both systems can only provide users with three-dimensional point coordinates and related strength information. The airborne small-spot full-waveform LiDAR system can record the entire backscattered echo waveform of the scatterer at a small sampling interval, and the user can extract more information through independent processing and analysis of the full waveform data.
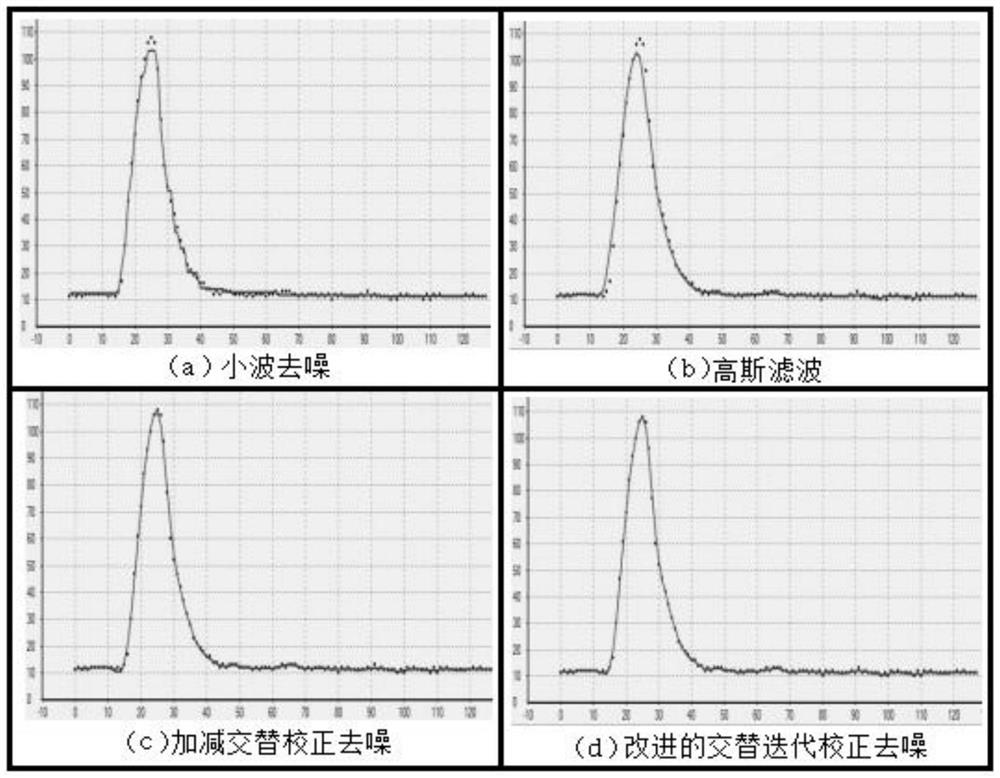
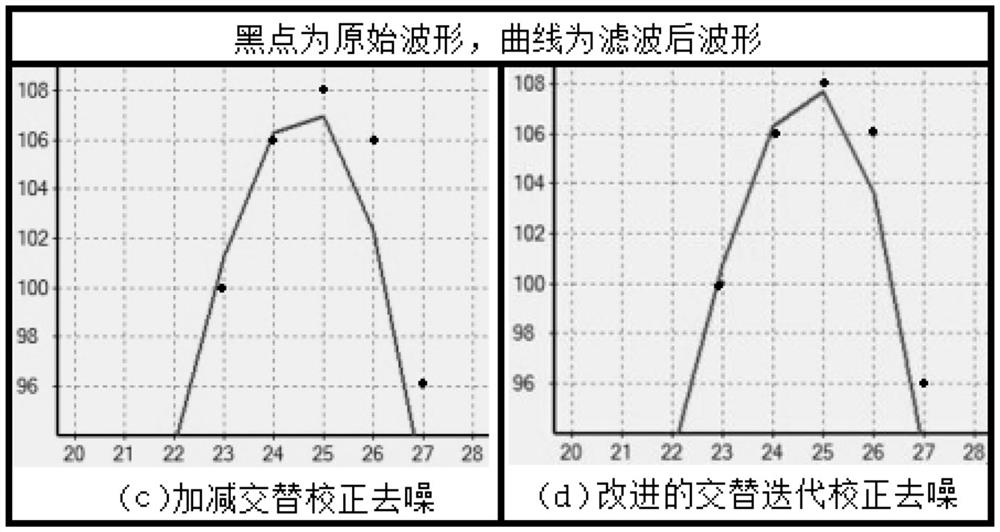
[0100] Based on the Gaussian properties of the airborne LiDAR full-waveform data, this application decompose...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com