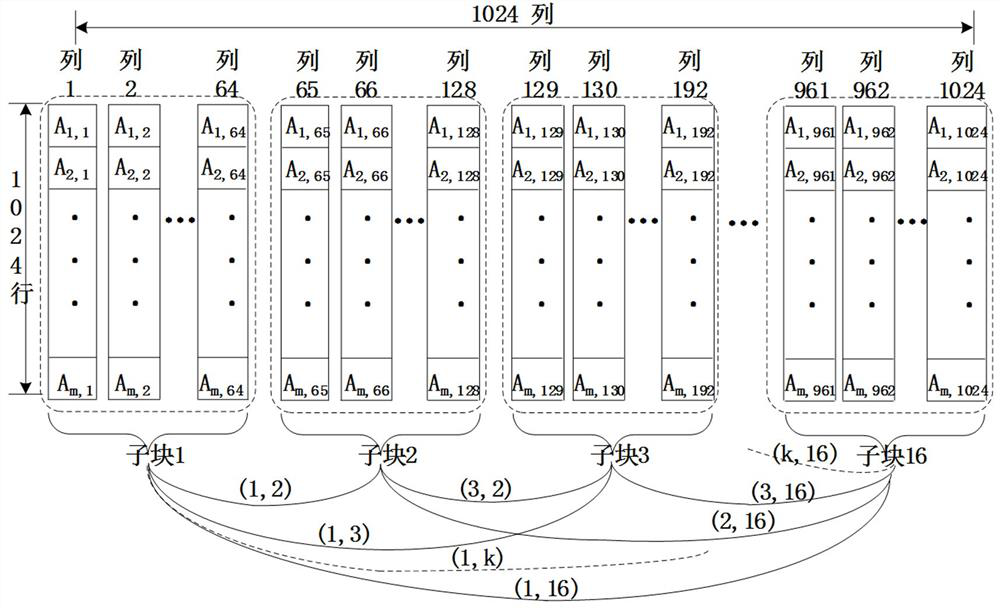
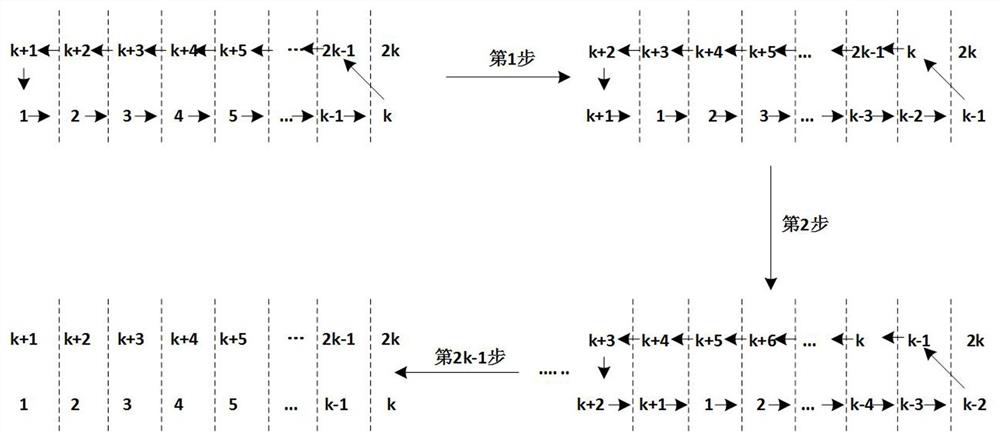
A Method for FPGA Accelerated Realization of Singular Value Decomposition of Matrix
A singular value decomposition and matrix singularity technology, applied in the field of signal processing, can solve problems such as FPGA development difficulties, huge workload, and small matrix size, and achieve the effects of easy FPGA development and implementation, reduced handling capacity, and improved parallel efficiency
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0021] The present invention will be described in detail below according to the accompanying drawings and preferred embodiments, and the purpose and effect of the present invention will become clearer. It should be understood that the specific embodiments described here are only used to explain the present invention, and are not intended to limit the present invention.
[0022] First give an explanation of the technical terms:
[0023] (1) FPGA: Field Programmable Gate Array Field Programmable Gate Array
[0024] (2) BRAM: Block RAM, FPGA internal block RAM
[0025] (3) Jacobi: In this invention, it refers specifically to unilateral Jacobi rotation, which is often used in FPGA-based matrix singular value decomposition
[0026] (4) round-robin: round-robin scheduling, a commonly used scheduling mechanism for unilateral Jacobi rotation singular value decomposition
[0027] (5) DRAM: Dynamic Random Access Memory, here specifically refers to off-chip DRAM, such as DDR3 (or DDR4)...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com