[0052] Below in conjunction with the accompanying drawings and specific embodiments, the technical solution is further described as follows:
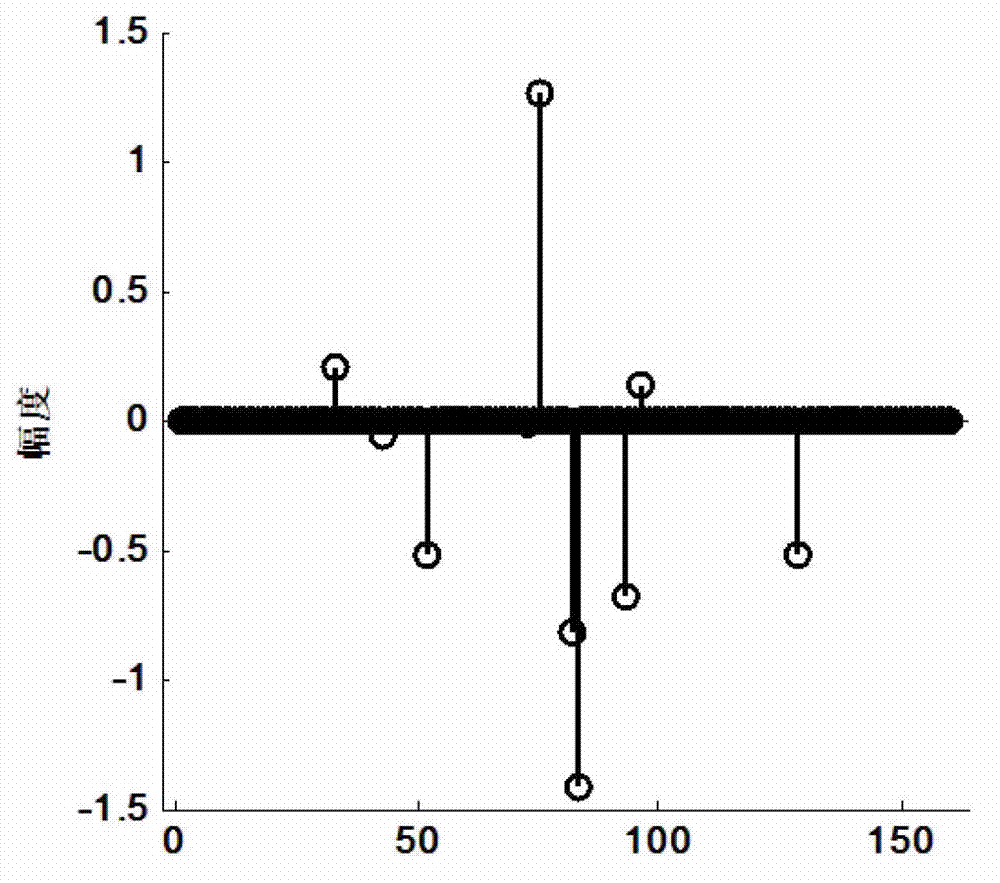
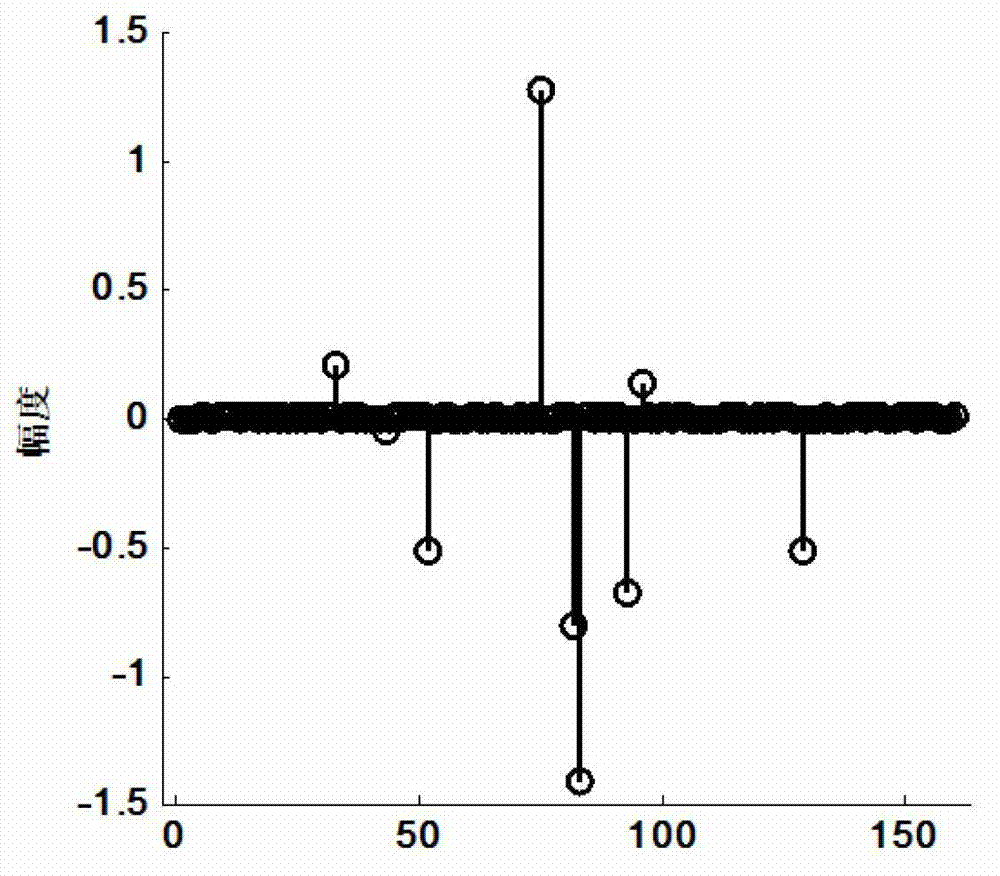
[0053] Filter-based compressed sensing signal acquisition method
[0054] In order to obtain the observation of "sampling while compressing", the typical physical implementation method of CS is random downsampling. [17] , analog information converter sampling [18] and random filter sampling [19] Wait. Reference [3] designs a dual-channel A/D random co-sampling based on the classical CS implementation principle, but the storage capacity of random number registers and the calculation of dimensionality reduction random projection are large, which affects the sampling efficiency.
[0055] The present invention considers the signal x∈R N Difference Equation Through Finite Impulse Response Filter
[0056] y ( i ) = Σ k = 0 L - 1 h ( k ) x ( i - k ) , i=1,...,M(4) (where h(0),...,h(L-1) are filter coefficients [20] ),
[0057] According to the literature [3], a filtering-based compressed sensing signal acquisition framework is designed to realize multi-channel A/D cooperative signal sampling, such as figure 1. Considering the complexity of hardware implementation in practical applications, dual-channel A/D co-sampling can be preferred.
[0058] Depend on figure 1 The signal sampling process is constructed as follows Toeplitz measurement matrix
[0059]
[0060] then observe i=1,...,M, where b 1 ,...,b L Can be seen as filter coefficients. By definition 1, the submatrix Φ FT The singular value of is the Grammian Matrix (Grammian Matrix) G(Φ F , T)=Φ′ FT Φ FT , the arithmetic roots of the eigenvalues. If it is verified that G(Φ F , all eigenvalues λ of T) i ∈(1-δ K , 1+δ K ), i=1,...,T, then Φ F Meet RIP, and can pass l 1 The optimization reconstructs the original signal with high probability. For this reason, Φ in the present invention is obtained from the conclusions of the literature [11][21] F Satisfy the theorem of RIP.
[0061] Lemma 1 [21] (Gales Fruiting Disk Theorem) Let the matrix H ∈ R N×N , then all its eigenvalues fall on the N disks of the plane D i ( H ) = { z | | z - h ii | ≤ Σ j = 1 , j ≠ i N | h ij | } , The union of i=1,...,N in, where h ii the center of the circle, r i = Σ j = 1 , j ≠ i N | h ij | is the radius.
[0062] Suppose there are integers K ≥ 1 and positive numbers δ d ,δ o make δ d +δ o =δ K ∈(0,1), and G(Φ F , T) of the diagonal element (diagonal element) and the off-diagonal element (off-diagonal elemem) satisfy |G ii (Φ F , T)-1| d and |G ij (Φ F , T)| o /K, then it can be known from Lemma 1: when the radius When, G(Φ F , the eigenvalue λ of T) i ∈(1-δ d -δ o , 1+δ d +δ o ) = (1-δ K , 1+δ K ), i=1,...,T.
[0063] Lemma 2 [11] Let {u i} is a sequence of random variables of i.i.d and satisfies |u i |≤a, E(u i )=0, then there are
[0064] P ( | Σ i = 1 M u i 2 - M σ 2 | ≥ t ) ≤ 2 exp ( - 2 t 2 M a 4 ) - - - ( 6 )
[0065] Lemma 3 [11] Let {u i} and {v i} is a sequence of random variables of i.i.d and satisfies |u i |≤a, |v i |≤a, |u i v i |≤a 2 , E(u i )=E(v i )=0, then there are
[0066] P ( | Σ i = 1 M u i v i | ≥ t ) ≤ 2 exp ( - t 2 2 M a 4 ) - - - ( 7 )
[0067] Theorem 1 Let {b l} is a sequence of random variables of i.i.d and satisfies b l ~N(0, 1/M), then When N≥3, make the pair ∀ M ≥ 32 K 2 c 2 δ K 2 - 32 c 2 c 1 log 3 ( N 2 - N ) Have
[0068]
[0069] Proof From equation (5), we know that Gram matrix G=Φ′ F Φ F The diagonal and off-diagonal elements of , respectively, are
[0070] G ij = b i b j + b i - 1 b j - 1 + · · · + b i - t j + 1 b j - t j + 1 1 ≤ i ≤ L , 1 ≤ j ≤ N ≤ b L b j + L - i + b L - 1 b j + L - i - 1 + · · · + b L - t j + 1 b j + L - i - t j + 1 L i ≤ N , i - L + 1 ≤ j ≤ i 0 L i ≤ N , 1 ≤ j i - L + 1
[0071] G ii = b i 2 + b i - 1 2 + · · · + b i - s i + 1 2 1 ≤ i ≤ L b L 2 + b L - 1 2 + · · · + b L - s i + 1 2 L i ≤ N - - - ( 9 )
[0072] where G ij =G ji , integer 1≤s i ≤M,1≤t j ≤M, i，j =1,…,N.
[0073] According to Lemma 2 and Equation (9), G ii (1≤i≤L) satisfy
[0074] P ( | G ii - E ( G ii ) | ≥ δ d ) = P ( | Σ l = i i - s i + 1 b l 2 - E ( Σ l = i i - s i + 1 b l 2 ) | ≥ δ d )
[0075] ≤ P ( | Σ l = i i - s i + 1 b l 2 - 1 | ≥ δ d ) ≤ 2 exp ( - 2 M 2 δ d 2 s i c 2 ) - - - ( 10 )
[0076] P ( | G ii - E ( G ii ) | ≥ δ d ) = P ( | Σ l = L L - s i + 1 b l 2 - E ( Σ l = L L - s i + 1 b l 2 ) | ≥ δ d ) ≤ P ( | Σ l = L L - s i + 1 b l 2 - 1 | ≥ δ d ) ≤ 2 exp ( - 2 M 2 δ D 2 s i c 2 ) - - - ( 11 )
[0077] From equations (10) and (11), we can get
[0078] P ( ∪ i = 1 N | G ii - 1 | ≥ δ d ) ≤ Σ i = 1 N 2 exp ( - 2 M 2 δ d 2 s i c 2 )
[0079] ≤ Σ i = 1 N 2 exp ( - 2 M 2 δ d 2 M c 2 ) = 2 Nexp ( - 2 M δ d 2 c 2 ) - - - ( 12 )
[0080] On the other hand, it can be seen from equation (9) that when 1≤i≤L, i-j=1, G ij = b i b i - 1 + b i - 1 b i - 2 + b i - 2 b i - 3 + b i - 3 b i - 4 + · · · + b i - t j + 1 b i - t j two adjacent terms in (such as b i b i-1 and b i-1 b i-2 ) is not independent, so Lemma 3 cannot be used directly, so consider t j Odd and even cases, respectively. when t j When it is odd, set G ij split into
[0081] G ij = G ij 1 + G ij 2 = ( b i b i - 1 + b i - 2 b i - 3 + · · · + b i - t j + 1 b i - t j ) + ( b i - 1 b i - 2 + b i - 3 b i - 4 + · · · + b i - t j b i - t j - 1 ) , in two adjacent terms in (such as b i b i-1 and b i-2 b i-3 or b i-1 b i-2 and b i-3 b i-4 ) are independent of each other, and Respectively and term, [ ] is the rounding function; when t j When it is even, set G ij split into
[0082] G ij = G ij 1 + G ij 2 = ( b i b i - 1 + b i - 2 b i - 3 + · · · + b i - t j + 1 b i - t j - 1 ) + ( b i - 1 b i - 2 + b i - 3 b i - 4 + · · · + b i - t j + 1 b i - t j ) , in and have item. Using Lemma 3, we have
[0083] P ( | G ij | ≥ δ o K ) ≤ P ( { | G ij 1 | δ o 2 K } or { | G ij 2 | δ o 2 K } )
[0084] ≤ 2 max { P ( | G ij 1 | δ o 2 K ) orP ( | G ij 2 | δ o 2 K ) }
[0085] ≤ 2 max { 2 exp ( - ( δ o / 2 K ) 2 2 q 1 ( c 2 / M 2 ) ) , 2 exp ( - ( δ o / 2 K ) 2 2 q 2 ( c 2 / M 2 ) ) }
[0086] ≤ 4 exp ( - ( δ o / 2 K ) 2 2 M ( c 2 / M 2 ) ) = 4 exp ( - M δ o 2 8 K 2 c 2 ) - - - ( 13 )
[0087] When 1≤i≤L, i-j>1, G ij The two adjacent terms in the ij Split as above. Similarly, when L ij =G ji , can be obtained from formula (13)
[0088] P ( ∪ i = 1 N ∪ j = 1 , j ≠ i N { | G ij | ≥ δ o K } ) ≤ Σ i = 1 N ( Σ j = 1 , j ≠ i N 4 exp ( - M δ o 2 8 K 2 c 2 ) ) ≤ 2 ( N 2 - N - M 2 + M ) exp ( - M δ o 2 8 K 2 c 2 ) - - - ( 14 )
[0089] Let δ d =δ o =δ K /2, N≥3, then there are
[0090]
[0091] = P ( ∪ i = 1 N | G ii - 1 | ≥ δ d ) + P ( ∪ i = 1 N ∪ j = 1 , j ≠ i N { | G ij | ≥ δ o K } )
[0092] ≤ 2 Nexp ( - 2 M δ d 2 c 2 ) + 2 ( N 2 - N - M 2 + M ) exp ( - M δ o 2 8 K 2 c 2 )
[0093] ≤ 3 ( N 2 - N ) exp ( - M δ K 2 32 K 2 c 2 ) - - - ( 15 )
[0094] All in all, yes ∀ M ≥ 32 K 2 c 2 δ K 2 - 32 c 2 c 1 log 3 ( N 2 - N ) Have
[0095]
[0096] = P ( ∪ i = 1 N | G ii - 1 | δ d ) + P ( ∪ i = 1 N ∪ j = 1 , j ≠ i N { | G ij | δ o K } ) ≥ 1 - exp ( - c 1 M K 2 ) - - - ( 16 )
[0097] in c 1 δ K 2 / 32 c 2 .
[0098] Theorem 1 explains Φ F RIP is satisfied with high probability, so by y=Φ F x can reconstruct the original signal with high probability through problem (2), where Φ F Only need to generate and store L random numbers, Φ F x requires M×L multiplication operations. However, the widely used random matrix Φ R Need to generate and store M×N random numbers, Φ R x requires M×N multiplication operations. It can be seen that the CS sampling process based on filtering is not only easy to implement in hardware, but also can greatly reduce the computational cost of the system, which is beneficial to the practical application of CS.
[0099] Preferably, CS is proposed for compressible signals such as actual speech and images: if the signal x has sparseness on the transform basis matrix Ψ, then the following 1 can be solved by solving 1 optimization problem
[0100] min α | | α | | 1 s . t . y = Φx = ΦΨα = Ξα - - - ( 17 )
[0101] The original signal is accurately reconstructed, in which Φ and Ψ are not correlated, and Ξ is called the CS matrix. Reference [16] defines the coherence between Φ and Ψ as And it is pointed out that when Φ and Ψ are irrelevant, that is, when μ is small, Ξ satisfies RIP with high probability and guarantees that there is a sparse solution to problem (17). In order to make Φ F The degree of coherence with the orthogonal matrix is as small as possible, and the present invention modifies Φ F in the following form:
[0102] Φ S = b 1 . . . b L 0 . . . . . . . . . . . . . . . 0 0 . . . 0 b 1 . . . b L 0 . . . . . . 0 . . . . . . . . . . . . . . . 0 . . . 0 . . . 0 . . . 0 b 1 . . . b L - - - ( 18 )
[0103] Sparse matrix Φ S By collecting the local information of the original signal, the original signal can be accurately reconstructed. This makes CS applicable to some practical scenarios, such as energy- and resource-constrained sensor networks. Each sensing device collects signals from the target in an independent sampling period, then all sampling signals are y=Φ S x, the convergence center reconstructs the original signal through problem (17), thereby reducing the working time and energy consumption of each sensing device.
[0104] The following proves Φ according to Theorem 1 S RIP is also satisfied with high probability.
[0105] Theorem 2 Let {b l} is a sequence of random variables of i.i.d and satisfies E(b l )=0, but When N≥2K, make the pair ∀ M ≥ 8 K 2 c 2 δ K 2 - 8 c 2 c 2 log 2 N 2 K Have
[0106]
[0107] The proof considers Φ S Gram matrix
[0108]
[0109] where B=[b 1 ,…,b L ], B ′ B = b 1 2 b 1 b 2 . . . b 1 b L b 2 b 1 b 2 2 . . . b 2 b L . . . . . . . . . . . . b L b 1 b L b 2 . . . b L 2 . According to Theorem 1, we can get
[0110] P ( ∪ i = 1 N | G ii - 1 | ≥ δ d ) ≤ Σ i = 1 N 2 exp ( - 2 M 2 δ d 2 c 2 ) = 2 Nexp ( - 2 M 2 δ d 2 c 2 ) - - - ( 21 )
[0111] P ( ∪ i = 1 N ∪ j = 1 , j ≠ i N { | G ij | ≥ δ o K } ) ≤ Σ i = 1 N ( Σ j = 1 , j ≠ i N 2 exp ( - M 2 δ o 2 2 K 2 c 2 ) ) ≤ ( N 2 M - N ) exp ( - M 2 δ o 2 2 K 2 c 2 ) - - - ( 22 )
[0112] Let δ d =δ o =δ K /2, N≥2K, then there is
[0113]
[0114] ≤ 2 Nexp ( - 2 M 2 δ d 2 c 2 ) + ( N 2 M - N ) exp ( - M 2 δ o 2 2 K 2 c 2 ) ≤ 2 N 2 K exp ( - M δ K 2 8 K 2 c 2 ) - - - ( 23 )
[0115] All in all, yes ∀ M ≥ 8 K 2 c 2 δ K 2 - 8 c 2 c 2 log 2 N 2 K Have
[0116]
[0117] in c 2 δ K 2 / 8 c 2 .
[0118] If Ψ is the identity matrix, it is easy to compare Theorem 1 and Theorem 2: Φ S than Φ F sparser, so Φ S The lower bound of the number of observations required is less than Φ F , so that through Φ S Carrying out CS sampling can improve the efficiency of signal acquisition.
[0119] Simulation results and analysis
[0120] The following simulation experiments are carried out on the Intel Core 2 processor to compare the computational overhead and reconstruction effect of CS sampling under Toplitz and random measurement matrices to verify the feasibility and effectiveness of the Toplitz measurement matrix.
[0121] 1. Reconstruction of sparse signals
[0122] Suppose a sparse signal x 0 ∈R N (N=160) There are K=10 non-zero elements, and the values and positions of the non-zero elements are randomly generated. The number of observations M in CS is closely related to the number of non-zero elements K, usually M=cK (c=3~4), and the compression ratio is defined as R=M/N. According to this, the observation y=Φ is generated F x 0 , where M=4K, R=1/4, Φ F random element b in l ~N(0,1/M). According to formula (4), in Fig. 2 based on Φ F and Φ R The calculation time of dimensionality reduction filtering sampling and dimensionality reduction random sampling is 2.4013e-004 seconds and 3.2328e-004 seconds, respectively, and the relative reconstruction error ε=||x 0 -x * || 2 /||x 0 || 2 are 1.6005e-011 and 6.7728e-014, respectively, both with good reconstruction results. According to the above method, an experiment is conducted to randomly generate 50 sparse signals for a fixed K. For different K and R, Fig. 3 gives the basis of Φ F and Φ R average sampling time of and the mean relative reconstruction error It can be seen from Figure 3 that with the increase of K and R, the required number of observations M also increases accordingly, so using Φ F and Φ R sampled and also increased accordingly, and increase is much greater than Obviously, this experimental result is the same as that in Section III about Φ F x and Φ R The theoretical analysis of the computational cost of x is consistent with the results. From Figure 3(b), it can be seen that based on Φ F and Φ R The original signal can be accurately reconstructed from the observation of , which shows that the Toeplitz matrix with simple hardware implementation and small storage capacity can achieve the same reconstruction performance as random sampling for filtering sampling with low computational cost. For different R, Figure 3(d) shows that when K=10, M≥4K, based on Φ F and Φ R of and are very small, and when M<4K, and are very large. This means that when M is small, that is, the sampling is too small, most of the information of the original signal cannot be obtained, so the original signal cannot be accurately reconstructed. Figure 3 shows the feasibility and practicality of filtering-based CS sampling.
[0123] 2. Reconstruction of compressible signals
[0124] To test based on Φ S Feasibility of CS sampling, using speech signal as experimental signal, where random element b l subject to a random uniform distribution. The experimental environment is a quiet environment, and the experimental objects are the voices of 4 speakers recorded by the Chinese Academy of Sciences Automation, two males and two females, with a sampling rate of 16kHz. The experiment is aimed at the "turbofan engine" whose test voices are female and male respectively. The rectangular window is used to divide the frames, and there is no overlap between the frames. The frame length is 160 samples/frame, and the average segmented signal-to-noise ratio SegSNR (dB )for:
[0125] SegSNR = 1 Nframe Σ i = 1 Nframe 10 × lg ( x i T X i ( x i - x i * ) T ( x i - x i * ) ) - - - ( 25 )
[0126] Among them, Nframe is the total number of frames of the original signal. The reconstructed signal is divided according to the size of the signal-to-noise ratio, and the signal with the signal-to-noise ratio is not greater than 0dB, 0~10dB, 10~20dB, 20~50dB, and greater than 50dB. good very good. The speech signal has approximate sparsity in the DCT domain, so the DCT basis is selected as Ψ [16]. When the compression ratio R=1/4, in Fig. 4 based on Φ S and Φ R The SegSNR of female voice: 29.0811dB, 14.9225dB, male voice: 46.0058dB, 30.5197dB, which shows that based on Φ S The reconstruction effect of speech signal is better than Φ R , the reason is that the female voice and the male voice are Φ S The coherence with DCT base 2.4918, 2.5281 is less than Φ R The coherence with the DCT basis is 3.8996 and 3.8272. The smaller the degree of coherence, the easier it is to use Equation (17) to search for the sparse solution α * and obtain the reconstructed signal x * =Ψα *, to make up for the deficiency that the DCT decomposition coefficient α of the speech signal is approximately sparse. On the other hand, the DCT decomposition coefficients of female voices have more high-frequency components, that is, the coefficients of female voices are not as concentrated in low frequencies, making their approximate sparsity weaker than male voices, so the reconstruction effect is not as good as male voices, but based on Φ S The reconstruction effect is still significantly better than Φ R.
[0127] Fig. 5 focuses on the study of different R and N based on Φ S and Φ R average sampling time of and SegSNR, the test speech is a long segment of speech consisting of 2 phrases randomly selected by the above 4 speakers, a total of 8 phrases, and is divided into frames by a rectangular window, and there is no overlap between the frames. It is easy to see from Figure 5 that with the increase of R and N, and also increased accordingly, and increase is much greater than The frame length is selected as 160 samples/frame, and Fig. 5(a)(b) studies the effect of R on the signal reconstruction performance. When R is larger, that is, the number of observations M is more, the SegSNR is higher, Φ R The lower signal reconstruction effect is better; while Φ S The lower signal reconstruction error fluctuates due to Φ S The following requirements are N=M×L, M=N×R. If the conditions are not met, for example, N×R is not an integer, then Φ S The number of elements in the last line is less than L, which reduces the amount of information captured in the original signal, thus affecting the reconstruction effect. To avoid this problem, construct Φ S When choosing the appropriate N, M and L according to R. For the same R, compare Φ S and Φ R The next SegSNR can be seen: even if Φ S The SegSNR fluctuates under the following conditions, but the reconstruction quality is good (20~50dB), and is greater than Φ R SegSNR under. When R≤1/4, Φ R The lower reconstruction quality drops rapidly from medium (10~20dB) to poor (0~10dB), which reflects Φ R The quality of the lower reconstruction is more sensitive to the number of samples M, and after the cooperation of M and L, Φ S The global information of the signal can be captured through local sampling, so that the reconstruction quality is less affected by M, which is convenient for practical CS sampling. Figure 5(c)(d) shows that when R=1/4, the above signal is in Φ S and Φ R SegSNR for different signal lengths N (ie different frame lengths) below. According to the R value, N is a multiple of 4, and Figure 5(d) shows Φ S The lower SegSNR tends to be stable, avoiding the problem of the reconstruction error fluctuation in Figure 3. The experimental results in Figures 4 and 5 show that based on Φ S The CS sampling of the R CS sampling.
[0128] Aiming at the problems of hardware realization, storage and calculation of random sampling in compressed sensing, the invention constructs a new filtering-based compressed sensing signal acquisition scheme based on the principle of finite impulse response filter, and constructs a corresponding Toeplitz measurement matrix, the new scheme reduces the hardware implementation difficulty and computational overhead of CS sampling. The theory of the present invention proves that the Toeplitz measurement matrix satisfies the RIP with a high probability, and it is easy to pass l 1 The optimal sparse solution is obtained by the optimization problem; meanwhile, the experiment verifies that the CS sampling based on the Toeplitz measurement matrix is superior to the random matrix in terms of sampling calculation cost and reconstruction performance, and is effective, feasible and applicable.
[0129] references
[0130] [1]DONOHO D L.Compressed sensing[J].IEEE Trans.on Information Theory,2006,52(4):1289-1306.
[0131] [2] E.Compressive sampling[C].International Congress of Mathematicians.European Mathematical Society PublishingHouse,Madrid,Spain,2006:1433-1452.
[0132] [3] Yu Kai, Li Yuanshi. Sound signal acquisition method based on compressed sensing. Chinese Journal of Instrumentation, 2012, 33(1): 105-112.
[0133] YU K,LI Y SH.New method for acoustic signal collection based on compressed sampling[J].Chinese Journal of ScientificInstrument,2012,33(1):105-112.
[0134] [4]CHEN W,WASSELL I J.Energy-efficient signal acquisition in wireless sensor networks: a compressive sensing framework[J].IET Wireless Sensor Systems,2012,2(1):1-8.
[0135] [5] FANG LY, LI S T, NIE Q. Sparsity based denoising of spectral domain optical coherence tomography images[J]. Biomedical Optics Express, 2012, 3(5): 927-942.
[0136] [6]SUN X L,YU A X,DONG Z.Three-dimensional SAR focusing via compressive sensing:the case study of angel stadium[J].IEEE Geoscience and Remote Sensing Letters,2012,9(4):759-763.
[0137] [7] Gu Bin, Yang Zhen, Hu Haifeng. Adaptive Wideband Spectrum Detection Based on Sequential Compressed Sensing. Journal of Instrumentation, 2011, 32(6): 1272-1277.
[0138] GU B,YANG Z,HU H F.Adaptive wide-band spectrum detection based on sequential compressed sensing[J].Chinese Journal ofScientifc Instrument,2011,32(6):1272-1277.
[0139] [8] CANDES E, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly in complete frequency information [J]. IEEE Trans. on Information Theory, 2006, 52(4): 489-509.
[0140] [9] RONALD A, DEVORE. Deterministic constructions of compressed sensing matrices [J]. Journal of Complexity, 2007, 23(4): 918-925.
[0141] [10]DO T T,TRANY T D,GAN L.Fast compressive sampling with structurally random matrices[J].IEEE International ConferenceAgouties,Speech and Signal Processing,Washington D.C.,USA,2008:3369-3372.
[0142] [11]HAUPT J,BAJWA W U,RAZ G.Toeplitz compressed sensing matrices with applications to sparse channel estimation[J].IEEETrans.on Information Theory,2010,56(11):5862-5875.
[0143] [12] WANG K, LIU Y L. RIP analysis for quasi-toeplitz CS matrices [C]. International Conference on Future Information Technology and Management Engineering, 2010, 2:223-226.
[0144] [13]MARCO D,MARK D.Single pixel imaging via compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):53-92.
[0145] [14] HEGDE C, WAKIN M, BARANIUK R. Random projections for manifold learning [C]. Neural Information Processing Systems (NIPS), Vancouver, Canada, 2007: 1-8.
[0146] [15]MONA S, OLGIEA M. Compressed sensing DNA microarrays, Rice ECE Department Technical Report TREE 0706, 2007.
[0147] [16] Ye Lei, Yang Zhen. Speech Compressed Sensing under Row Echelon Observation Matrix and Dual Affine Scale Interior Point Reconstruction Algorithm. Chinese Journal of Electronics, 2012, 40(3): 429-434.
[0148]YE L,YANG Z.Compressed sensing of speech signal based on special row echelon measurement matrix and dual affine scalinginterior point reconstruction method[J].Acta Electronica Sinica,2012,40(3):429-434.
[0149] [17] WANG X Z, WEI E I. Random sampling using shannon interpolation and poisson summation formulae. http://arxiv.org/abs/0909.2292.
[0150] [18] LASKA J N, KIROLOS S, DUARTE M F. Theory and implementation of an analog-to-information converter using random demodulation [C]. IEEE International Symposium on Circuits and Systems. New Orleans, USA. 2007: 1959-1962.
[0151] [19] TROPP J A, WAKIN M B, DUARTE M F. Random filters for compressive sampling and reconstruction, IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Toulouse, France, 2006: 872-875.
[0152] [20] Translated by Liu Shutang. Signals and Systems. Xi'an Jiaotong University Press, 1998.
[0153] LIU S T.Signals$Systems[M].Xianjiaotong University Press,1998.
[0154] [21] Li Xin, He Chuanjiang. Matrix Theory and Its Application. Chongqing University Press, 2005.
[0155] LI X, HE C J. Matrix theory and its application[M]. Chongqing University Press, 2005.
