Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

WiFi indoor locating method based on domain clustering

An indoor positioning and clustering technology, which is applied in the direction of instruments, measuring devices, and re-radiation, can solve the problems of position estimation accuracy, AP selection algorithm performance, and the fuzzy definition of the optimal AP subset number. The effect of precision and reliability

Inactive Publication Date: 2017-05-31
WUHAN UNIV
View PDF1 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] In general, the performance of the AP selection algorithm is affected by different environments, and the definition of the number of optimal AP subsets is often vague and has a certain impact on the accuracy of position estimation.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • WiFi indoor locating method based on domain clustering
  • WiFi indoor locating method based on domain clustering
  • WiFi indoor locating method based on domain clustering

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0019] In order to facilitate those of ordinary skill in the art to understand and implement the present invention, the present invention will be described in further detail below in conjunction with the accompanying drawings and embodiments. It should be understood that the implementation examples described here are only used to illustrate and explain the present invention, and are not intended to limit this invention.

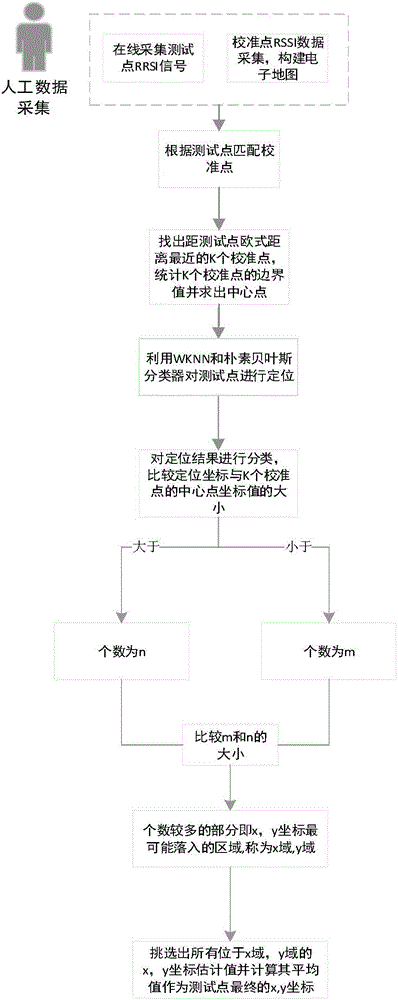
[0020] please see figure 1 , a kind of WiFi indoor positioning method based on domain clustering provided by the present invention, comprises the following steps:

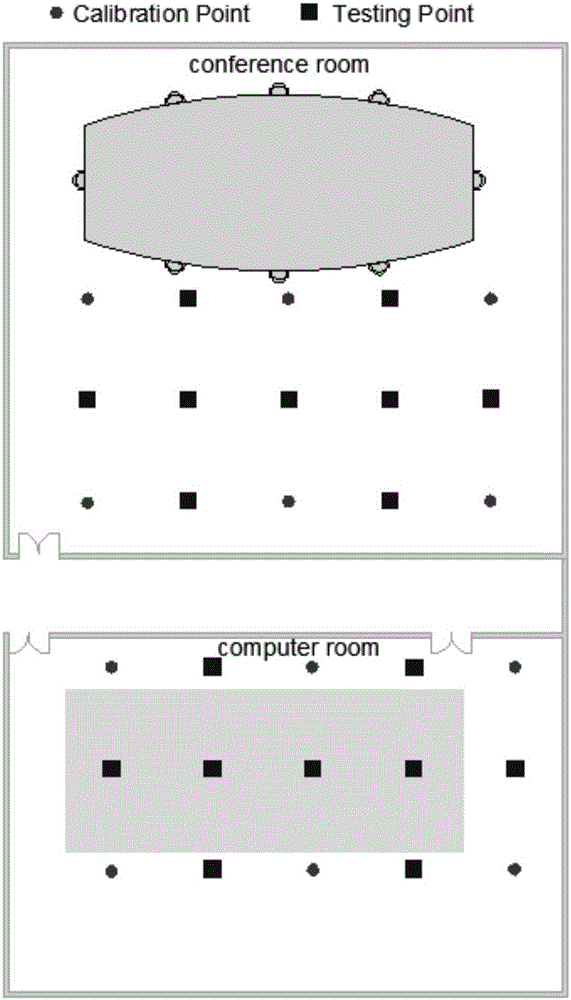
[0021] Step 1: Select 6 calibration points in two different indoor environments (see figure 2 ), collect the WiFi signal strength information at the calibration point, and the duration is 2min; associate the signal strength information with the location information of the calibration point to form a location fingerprint, and obtain the location fingerprint library;

[0022] Step 2: Collect WiFi...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a WiFi indoor locating method based on domain clustering. The method comprises the following steps: firstly selecting a plurality of reference points in two different indoor environments to serve as calibration points, collecting the WiFi signal strength information at the calibration points, and associating the signal strength information with the position information of the calibration points to form position fingerprint so as to obtain a position fingerprint library; then collecting the WiFi signal strength information of a test point, performing pre-matching on the WiFi signal strength information of the test point with the position fingerprint library, and finding K adjacent calibration points closest to the test point by using Euclidean distances of the calibration points and the test point; counting the boundary values of the K adjacent calibration points, and figuring out a central point; then locating the test point by using a WKNN or Naive Bayesian classifier; and m AP are observed by the calibration points and the test point in total, obtaining possible positions of the m test points; and finally determining a final position of the test point. Locating results tested in different indoor environments prove that the WiFi indoor locating method provided by the invention has better performance.

Description

technical field [0001] The invention belongs to the technical field of indoor positioning, and in particular relates to a new WIFi fingerprint-based method for indoor position positioning through area clusters. Background technique [0002] In the last two decades, location-based services for more and more personalized indoor environments have stimulated the development of various indoor positioning systems (IPS). A range of different positioning technologies are deployed for indoor position estimation, such as GNSS, ultrasound, ultra-wideband (UWB) and WiFi. There are two main challenges in WiFi indoor positioning technology: multipath effect and non-line-of-sight (NLOS) effect. Therefore, most WiFi indoor positioning systems use fingerprint technology for position estimation, which consists of two stages: a calibration stage (offline stage) and a positioning stage (online stage). The calibration phase builds a fingerprint of the location area by correlating the WiFi sign...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04W64/00G01S11/06
CPCH04W64/00G01S11/06
Inventor 张伟花向红邱卫宁贺小星刘少伟
Owner WUHAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com