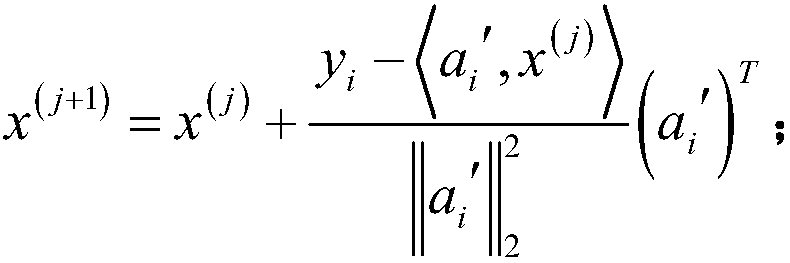Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Compressed sensing data reconstruction method based on randomized Kaczmarz iteration

A data reconstruction and compressed sensing technology, applied in code conversion, electrical components, etc., can solve the problems of low precision and slow reconstruction of compressed sensing data, so as to strengthen the reconstruction effect, improve the reconstruction accuracy, and regenerate the data. The effect of increasing construction speed

Inactive Publication Date: 2018-03-16
东北大学秦皇岛分校
View PDF3 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The object of the present invention is to provide a method for reconstructing compressed sensing data based on random Kaczmarz iterations, which can effectively solve the problems in the prior art, especially the slow speed and low precision of reconstructing compressed sensing data The problem

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Compressed sensing data reconstruction method based on randomized Kaczmarz iteration
  • Compressed sensing data reconstruction method based on randomized Kaczmarz iteration
  • Compressed sensing data reconstruction method based on randomized Kaczmarz iteration

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

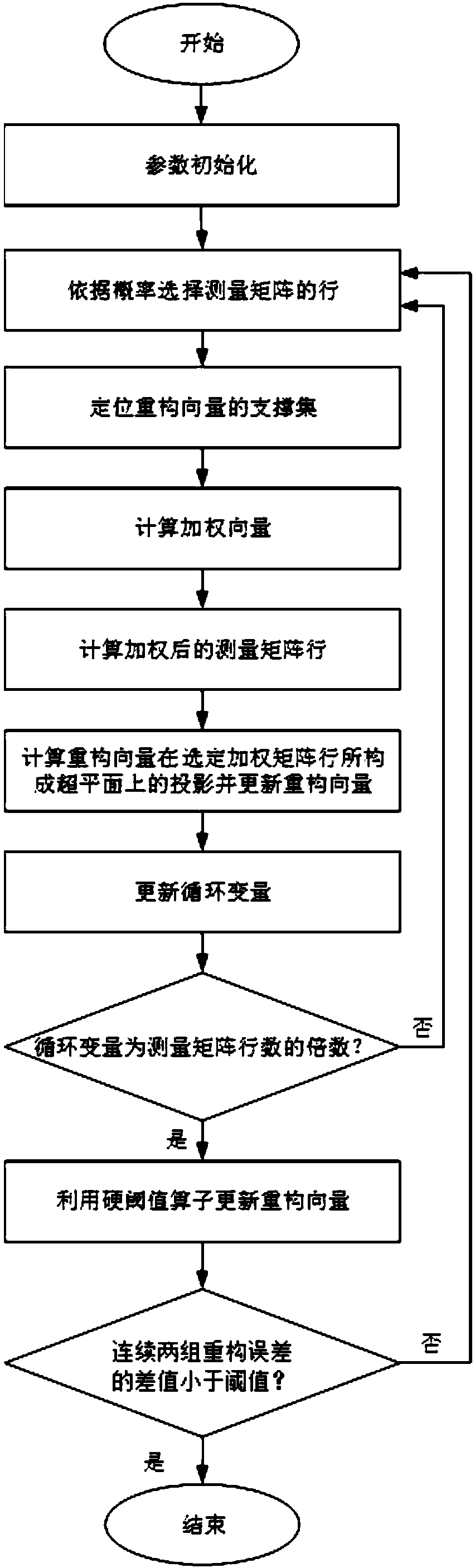
[0038]Embodiment 1 of the present invention: the compressed sensing data reconstruction method based on random Kaczmarz iteration, such as figure 1 shown, including the following steps:

[0039] First, adaptively change the weight of each row vector in the measurement matrix, and calculate the weighted measurement matrix row;

[0040] Second, the weighted measurement matrix rows are used to update the original data vector to be reconstructed in a sparse random Kaczmarz iterative manner;

[0041] Again, use the hard threshold operator to process the updated original data vector to be reconstructed, keep the first k' elements with the largest absolute value, and set the remaining elements to zero; the k' is the original data vector to be reconstructed The sparsity of the data vector;

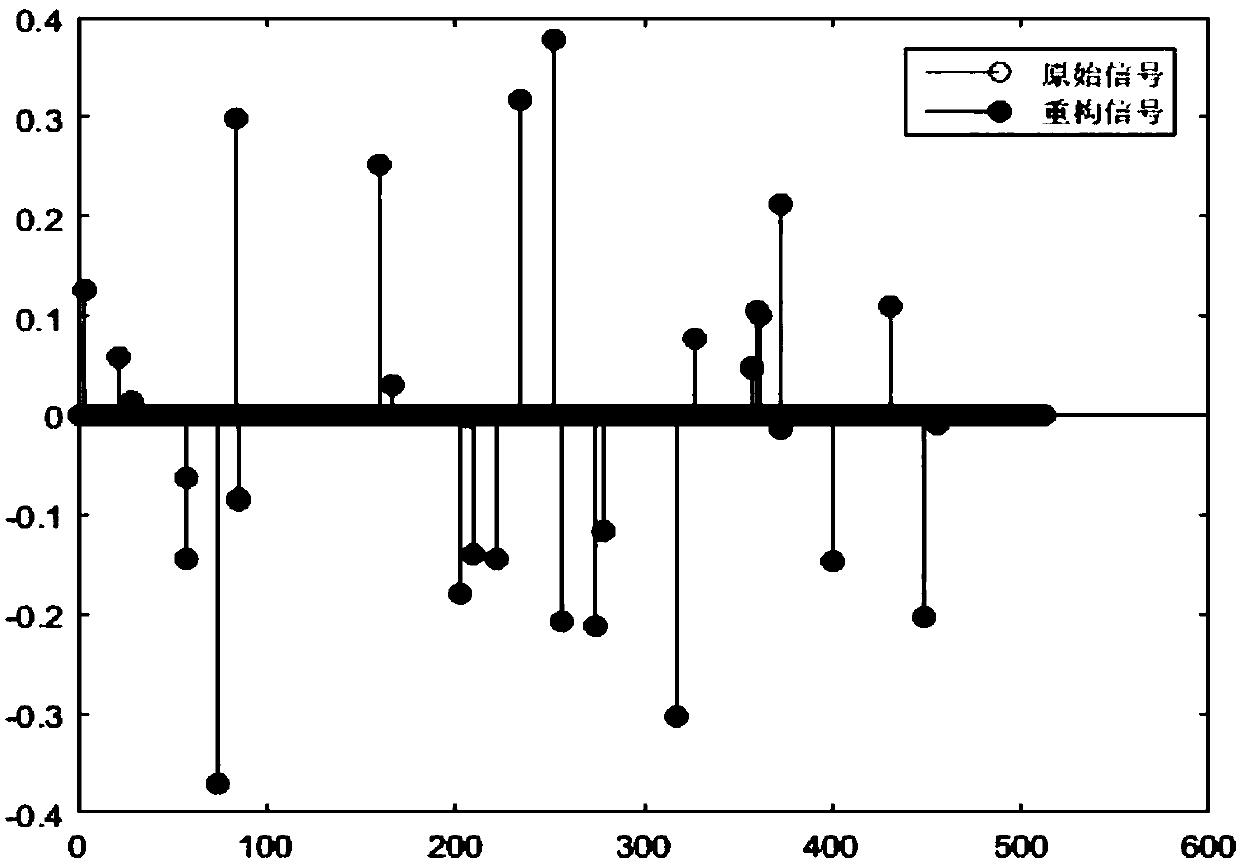
[0042] Finally, when the error difference between two adjacent data reconstruction results is smaller than the threshold, the final reconstruction result is obtained.

[0043] Specifically incl...

Embodiment 2

[0054] Embodiment 2: A method for reconstructing compressed sensing data based on random Kaczmarz iterations, comprising the following steps:

[0055] First, adaptively change the weight of each row vector in the measurement matrix, and calculate the weighted measurement matrix row;

[0056] Second, the weighted measurement matrix rows are used to update the original data vector to be reconstructed in a sparse random Kaczmarz iterative manner;

[0057] Again, use the hard threshold operator to process the updated original data vector to be reconstructed, keep the first k' elements with the largest absolute value, and set the remaining elements to zero; the k' is the original data vector to be reconstructed The sparsity of the data vector;

[0058] Finally, when the error difference between two adjacent data reconstruction results is smaller than the threshold, the final reconstruction result is obtained.

[0059] Among them, the weight of each row vector in the measurement m...

Embodiment 3

[0062] Embodiment 3: A method for reconstructing compressed sensing data based on random Kaczmarz iterations, comprising the following steps:

[0063] First, adaptively change the weight of each row vector in the measurement matrix, and calculate the weighted measurement matrix row;

[0064] Second, the weighted measurement matrix rows are used to update the original data vector to be reconstructed in a sparse random Kaczmarz iterative manner;

[0065] Again, use the hard threshold operator to process the updated original data vector to be reconstructed, keep the first k' elements with the largest absolute value, and set the remaining elements to zero; the k' is the original data vector to be reconstructed The sparsity of the data vector;

[0066] Finally, when the error difference between two adjacent data reconstruction results is less than the threshold, the final reconstruction result is obtained;

[0067] The weight of each row in the described self-adaptive change meas...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a compressed sensing data reconstruction method based on randomized Kaczmarz iteration. The method comprises the following steps: firstly, adaptively changing the weight of each row vector in a measurement matrix, and calculating weighted measurement matrix rows; secondly, updating original data vectors to be reconstructed through the weighted measurement matrix rows in themanner of sparsely randomized Kaczmarz iteration; thirdly, processing the updated original data vectors to be reconstructed through hard threshold operators, reserving first k' elements with the largest absolute values, and zeroing remaining elements; and lastly, obtaining a final reconstruction result when the difference between errors of two adjacent data reconstruction results is smaller thana threshold. The method provided by the invention has the advantages that the weight of the measurement matrix is adaptively adjusted according to data characteristics, and the vectors to be reconstructed are updated through the weighted measurement matrix, so that reconstruction effects for key elements in original signals are strengthened, the compressed sensing data reconstruction precision isimproved, and compressed sensing data reconstruction is accelerated.

Description

technical field [0001] The invention relates to a compressed sensing data reconstruction method based on random Kaczmarz iteration, and belongs to the technical field of compressed sensing data reconstruction. Background technique [0002] With the rapid development of information technology, a large amount of observation data needs to be collected and transmitted in signal processing, image processing and other application fields. A higher sampling rate not only has higher requirements for sensors, analog-to-digital conversion circuits, etc., but also consumes a large network bandwidth and storage space when transmitting and storing observation data. Therefore, how to achieve high-efficiency and energy-saving compressed data acquisition and accurately reconstruct the original data is of great significance. [0003] The patent application with the application number 201510062912.6 discloses a bridge moving vehicle load identification method based on the Kaczmarz algebraic i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H03M7/30
CPCH03M7/3062
Inventor 李国瑞
Owner 东北大学秦皇岛分校
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com