Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for establishing model for obtaining glomerular filtration rate and application

A technology of glomerular filtration rate and establishment method, which can be applied in medical simulation, health index calculation, medical informatics and other directions, and can solve the problem of inaccurate estimation of glomerular filtration rate.

Active Publication Date: 2019-03-29
THE THIRD XIANGYA HOSPITAL OF CENT SOUTH UNIV
View PDF4 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The technical problem to be solved by the present invention is: inaccurate estimation of glomerular filtration rate for the Chinese population

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for establishing model for obtaining glomerular filtration rate and application
  • Method for establishing model for obtaining glomerular filtration rate and application
  • Method for establishing model for obtaining glomerular filtration rate and application

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0027] In order to make the above objects, features and advantages of the present invention more comprehensible, specific implementations of the present invention will be described in detail below in conjunction with the accompanying drawings. In the following description, numerous specific details are set forth in order to provide a thorough understanding of the present invention. However, the present invention can be implemented in many other ways different from those described here, and those skilled in the art can make similar improvements without departing from the connotation of the present invention, so the present invention is not limited by the specific implementations disclosed below.

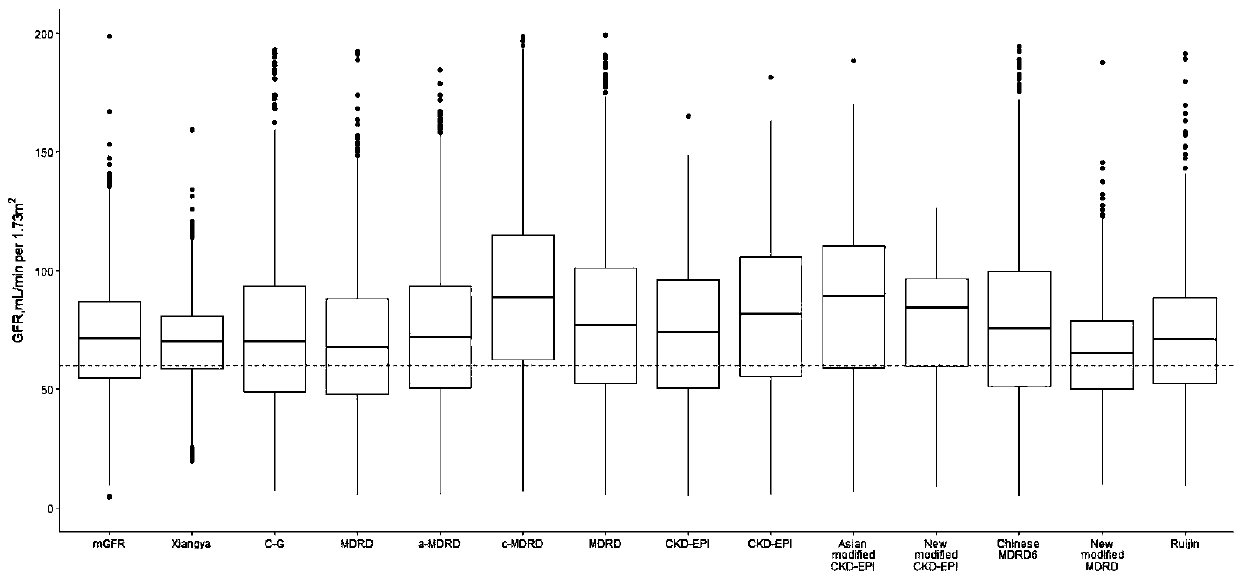
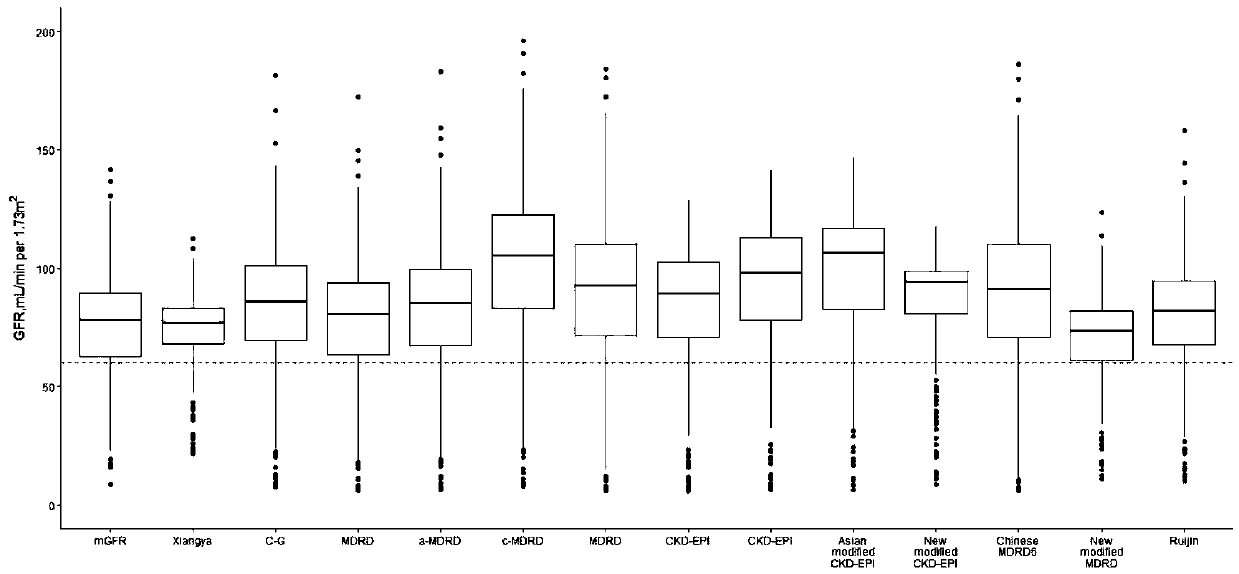
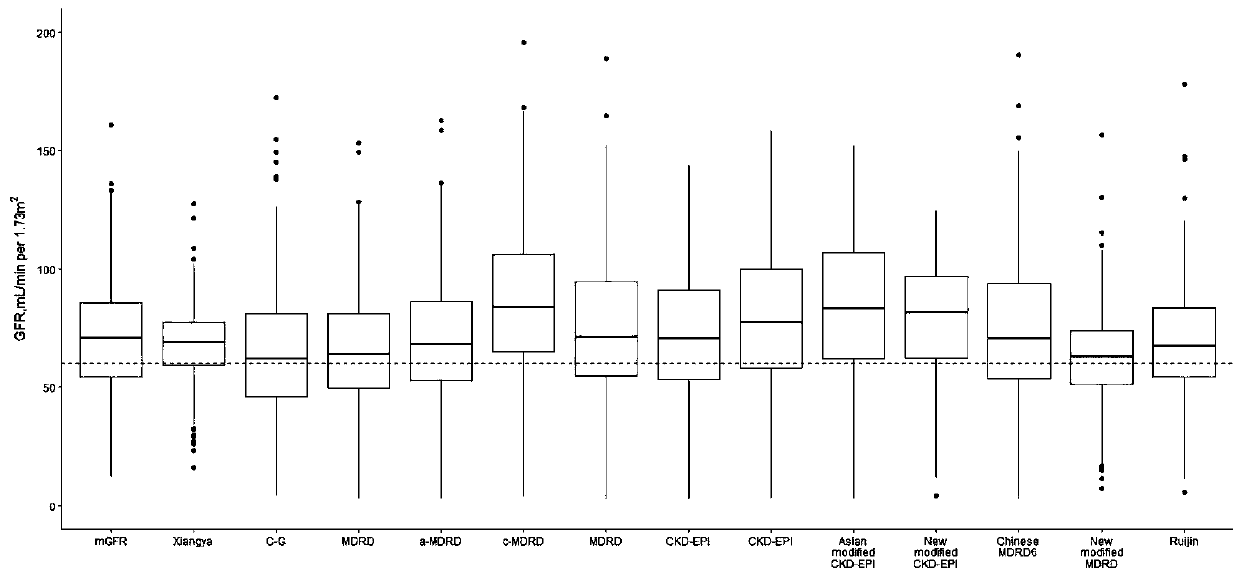
[0028] The patient data collected in this specific embodiment comes from the Third Xiangya Hospital (TXH) and the Second Xiangya Hospital (SXH) of Central South University (Changsha, Hunan Province) in central China (Changsha City, Hunan Province), and the First Affiliated Hospital (FX...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a method for establishing a model for obtaining the glomerular filtration rate of Chinese population and the application thereof. The establishing method comprises the following steps: S1, carrying out single factor analysis on a plurality of candidate independent variables corresponding to the glomerular filtration rate known by a patient by using least square method linear regression, and screening out a plurality of first independent variables; S2, carrying out multielement analysis on the first independent variables by using multiple linear regression modeling, andsimplifying the quantity of the first independent variables to establish a first model, wherein the function expression of the first model is GFR=94047.95*0.8892828*N<-0.22630>*C<-0.52474>*L<-0.92495>*H<0.28309>, GFR indicates the glomerular filtration rate, a is a coefficient related to sex, L indicates the concentration of creatinine, L indicates the concentration of chlorine ions, and H indicates the concentration of red cells. The model can accurately obtain the glomerular filtration rate of patients in Chinese population. The invention discloses the application of the model for obtaining the glomerular filtration rate of Chinese population in obtaining the glomerular filtration rate of Chinese population.

Description

technical field [0001] The invention relates to the field of medical and health technologies, in particular to a method for establishing a model for obtaining glomerular filtration rate and its application. Background technique [0002] Kidney disease is a worldwide public health disease with a high incidence and heavy burden. In 2012, there were 120 million chronic kidney disease patients in my country, with an incidence rate of 10.8%. Among hospitalized patients in China, acute kidney injury (AKI) accounted for 2.4%–8.1% of complications, and the mortality rate of patients with acute kidney injury was as high as 18.6%. –28.5%. In China, the average annual treatment cost per dialysis patient is US$14,000. Therefore, rapid and accurate assessment of renal function and changes in renal function is essential for the prevention, diagnosis and treatment of renal diseases. The glomerular filtration rate (Glomerular Filtration Rate, GFR) is the most accurate indicator for evalua...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G16H50/30G16H50/50
CPCG16H50/30G16H50/50
Inventor 左笑丛易翼虎尹文俊李岱阳张毕奎赵军朱超男
Owner THE THIRD XIANGYA HOSPITAL OF CENT SOUTH UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com