Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Construction of two wing and four wing coexistent chaotic system and design of fractional order circuit thereof

A chaotic system, fractional-order technology, applied in general control systems, control/regulation systems, instruments, etc., can solve problems such as high control costs and inability to achieve expected results, and achieve broad application prospects.

Inactive Publication Date: 2019-04-26
CHONGQING UNIV OF POSTS & TELECOMM
View PDF4 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At present, most of the studies on the stability and synchronization of fractional order chaotic systems are based on active control strategies. Although this method can achieve the purpose of synchronization, the control cost is relatively high, and for systems with unknown parameters, this method cannot achieve expectations. Effect

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Construction of two wing and four wing coexistent chaotic system and design of fractional order circuit thereof
  • Construction of two wing and four wing coexistent chaotic system and design of fractional order circuit thereof
  • Construction of two wing and four wing coexistent chaotic system and design of fractional order circuit thereof

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0026] Specific implementation mode 1: This implementation mode describes in detail a three-dimensional chaotic system in which two-wing and four-wing attractors coexist and its dynamic characteristics:

[0027] 1. A construction method of a chaotic system with two wings and four-wing attractors coexisting, characterized in that, comprising the following steps:

[0028] S(1) Construct a three-dimensional chaotic system (1) with coexistence of two-wing and four-wing attractors, whose mathematical model is described as:

[0029]

[0030] Where x, y, z are system variables, system parameters a=0.8, b=7, c=-10. When the initial value is [2, 2, 2], the three Lyapunov exponents of the system are 1.3952, -0.0013, -4.9953. Because its maximum exponent is greater than 0, the system is a chaotic system.

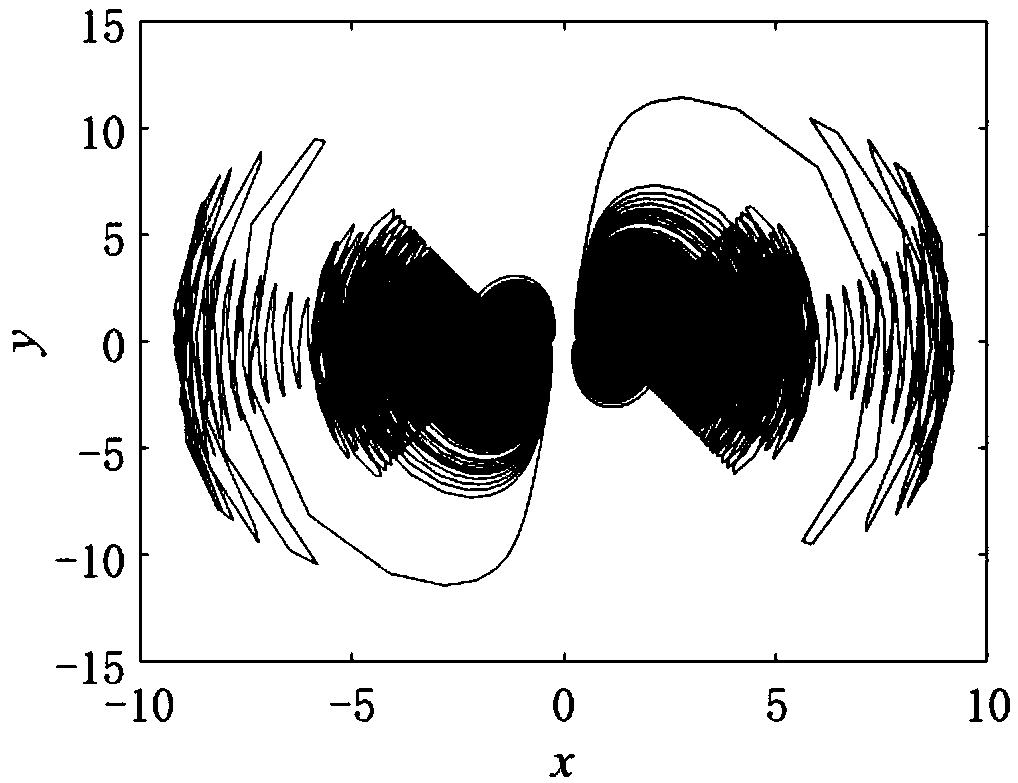
[0031] When the initial values ​​are [2, 2, 2] and [-2, -2, 2], there are two isolated two-winged chaotic attractors in the system, such as figure 1 shown. When the initial valu...

specific Embodiment approach 2

[0046] Specific implementation mode 2: This implementation mode describes in detail the implementation of the analog circuit of the fractional-order system with coexistence of two-wing attractors proposed by the present invention:

[0047] 2. A construction method of a fractional order chaotic system with two wings attractors coexisting and its analog circuit realization, it is characterized in that comprising the following steps:

[0048] S(1) is defined according to the Caputo fractional-order integral, and the 0.8-order fractional-order system model corresponding to system (1) can be obtained as:

[0049]

[0050] Where a=0.8, b=7, c=-10, 0

[0051] When the initial values ​​are [1, 1, 1] and [-1, -1, -1], there are two isolated two-wing chaotic attractors in the system, such as Figure 5 shown. When the initial value is [1, 1, 1], the maximum Lyapunov exponent spectrum is obtained as Figure 6shown.

[0052] S(2) Usin...

specific Embodiment approach 3

[0063] Specific embodiment three: This embodiment describes in detail the realization of the adaptive synchronization control of the fractional order system proposed by the present invention:

[0064] 3. the adaptive synchronous control realization of a kind of fractional order system is characterized in that, comprises the following steps:

[0065] (1) Based on the fractional-order system model designed in Scheme 2, construct the fractional-order drive system and response system.

[0066] (2) According to the definition of the synchronous error of the drive system and the response system, construct the synchronous error system.

[0067] (3) Design adaptive controller and parameter update law, use mathematical theory to prove the synchronization property, and use MATLAB program to simulate and verify synchronization.

[0068] Further, the adaptive synchronous control method of the fractional order system according to the present invention, its specific steps are as follows: ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to construction of a two wing and four wing coexistent chaotic system and design of a fractional order system simulation circuit thereof. In order to make dynamic characteristicsof a fractional order chaotic system more complex, a novel two wing and four wing attractor coexistent integer order chaotic system is firstly designed, and since coexistence attractors are complex,application value is higher in the fields of information encryption and secret communication. Secondarily, on the basis of the system, a fractional order system is constructed, the simulation circuitof the fractional order system is designed, and a circuit simulation result and a numerical value simulation result are uniform. The correctness of theoretical analysis of the fractional order systemand realizability of actual physics of the fractional order system are verified. Finally, based on a fractional order system mode, a self-adaptation synchronous controller and a parameter updating lawof the fractional order system are designed, synchronization of a driving system and a responding system is realized in numerical value simulation, and a new selection is provided for further application of the fractional order system to the field of communication engineering.

Description

technical field [0001] The invention relates to a chaotic system and its circuit, in particular to the circuit design and self-adaptive synchronous control technology of the fractional order chaotic system. Background technique [0002] Chaos is a unique form of motion in nonlinear dynamic systems, and it has been widely used in neural network, ultrasonic guided wave detection, secure communication, bioengineering and other fields. Compared with systems without coexisting attractors, chaotic systems with coexisting attractors have more complex dynamic behaviors and have broader application prospects in the field of information encryption. [0003] Compared with integer-order chaotic systems, fractional-order chaotic systems can more objectively reveal and describe the dynamic behavior of actual systems, so fractional-order chaotic systems have higher research value. [0004] The synchronization of fractional order chaotic systems has more prominent application value in the ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 徐昌彪郭桃桃扶坤荣
Owner CHONGQING UNIV OF POSTS & TELECOMM
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com