Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Transfer matrix calculation stability optimization method based on dimensionless analysis

A transfer matrix, dimensionless technology, applied in complex mathematical operations, geometric CAD, CAD numerical modeling, etc., can solve problems such as high-frequency unstable transfer matrices, to achieve programming calculations, high precision, and solve calculation instability problem effect

Active Publication Date: 2020-02-18
HARBIN ENG UNIV
View PDF4 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The purpose of the present invention is to provide a transfer matrix calculation stability optimization method based on non-dimensional analysis for solving the problem of high-frequency instability in the dynamic calculation of the transfer matrix method for one-dimensional elastic structures such as pipes and beams

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Transfer matrix calculation stability optimization method based on dimensionless analysis
  • Transfer matrix calculation stability optimization method based on dimensionless analysis
  • Transfer matrix calculation stability optimization method based on dimensionless analysis

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0055] The present invention is described in more detail below in conjunction with accompanying drawing example:

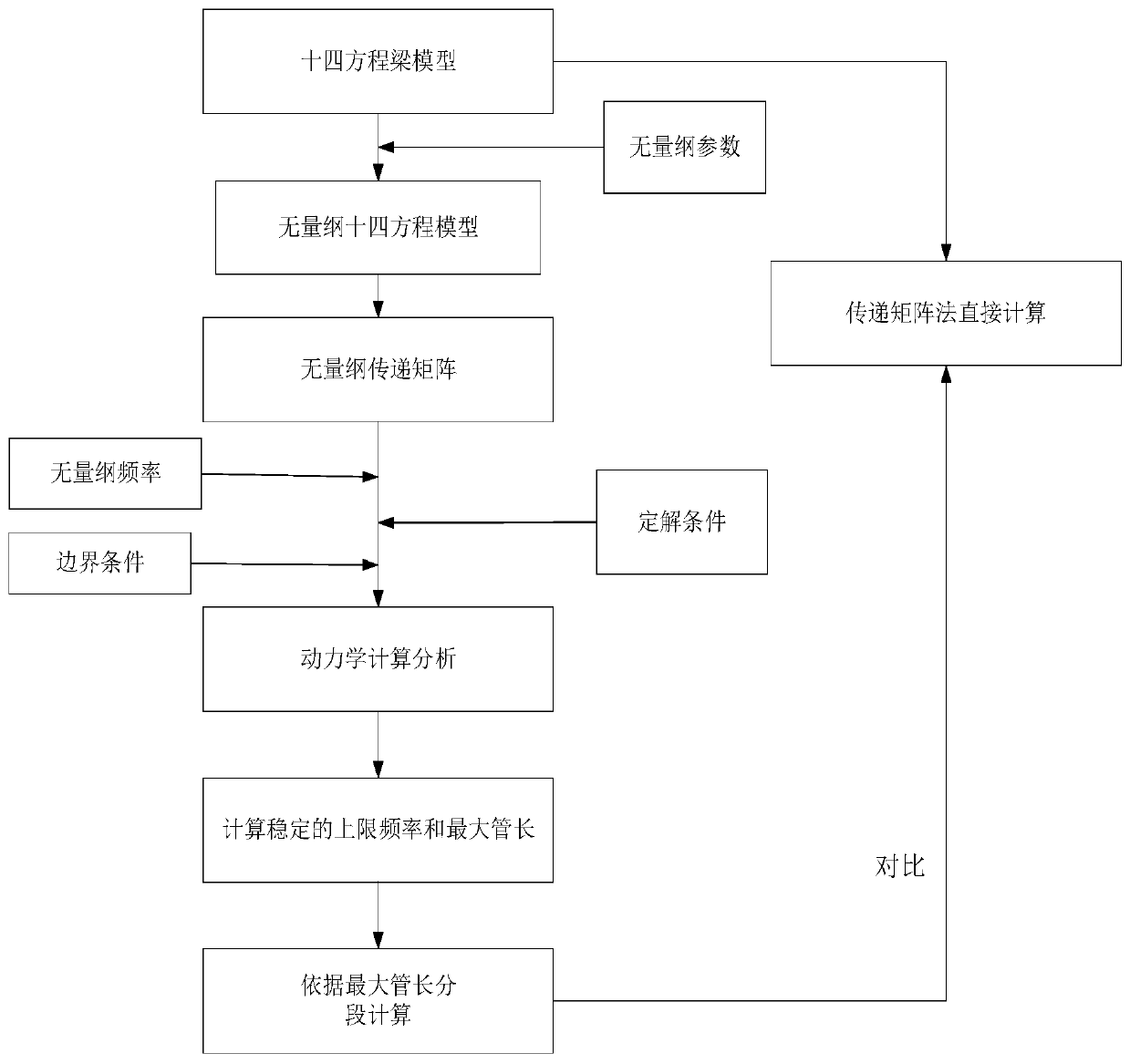
[0056] to combine Figure 1-6b , the computational stability optimization method of the present invention comprises the following steps:

[0057] (1) Establishment of dimensionless mathematical model

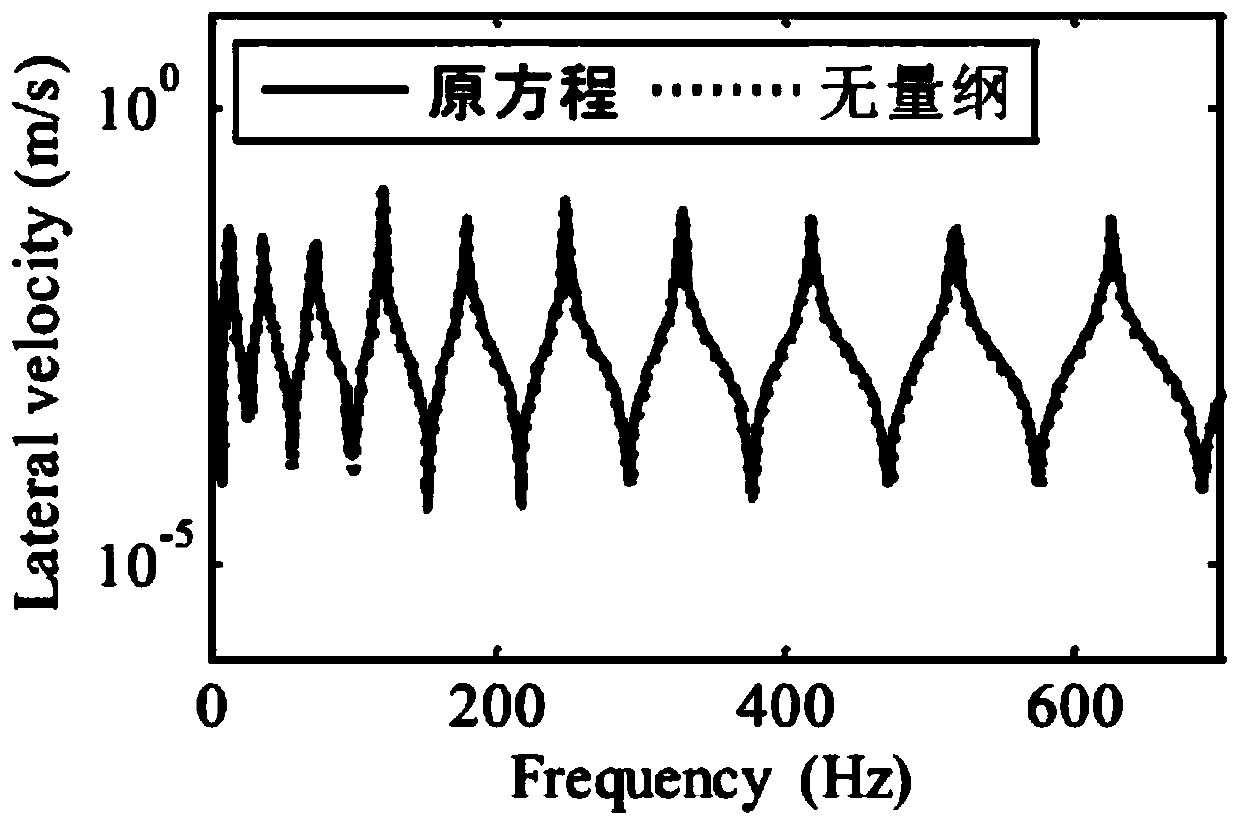
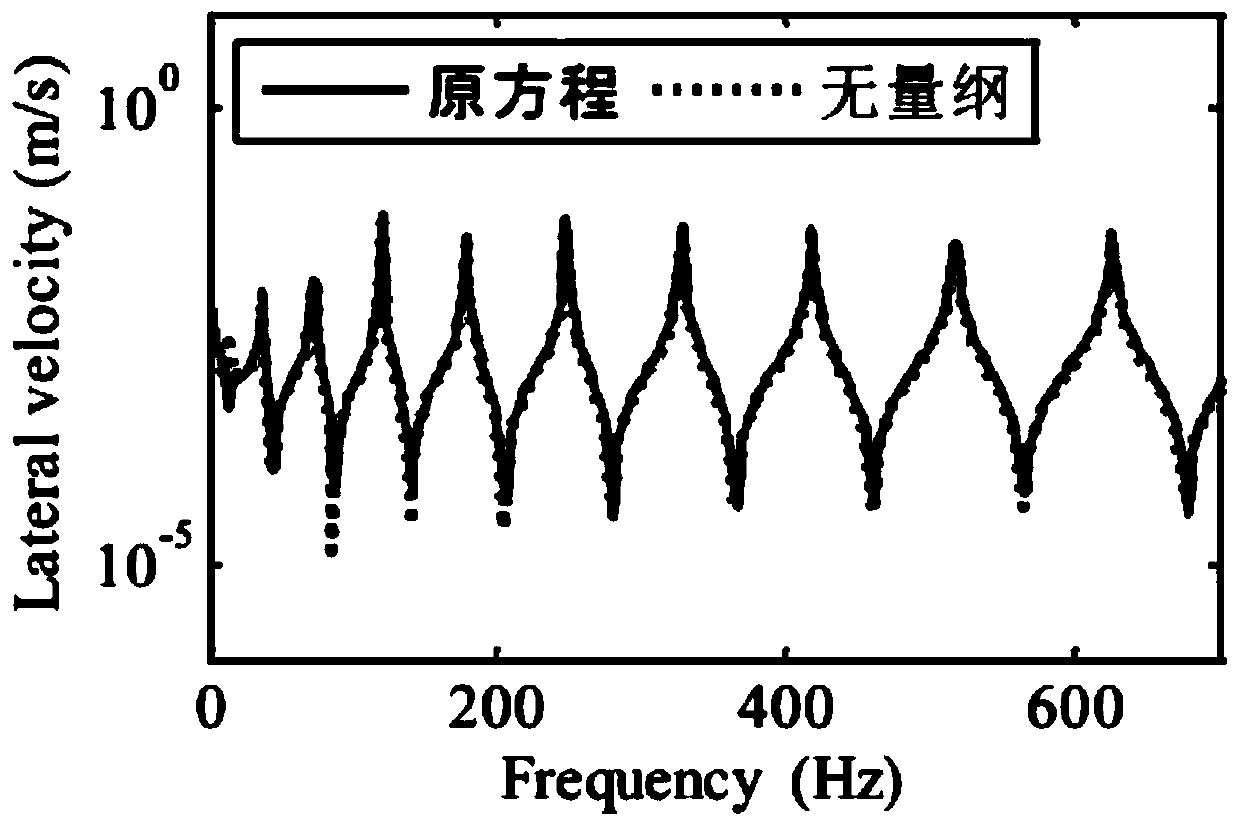
[0058]The accuracy factors affecting the calculation of the transfer matrix method can be summed up in terms of frequency, fluid quality, Young's modulus of elasticity, pipe diameter, and pipe length. Through dimensional analysis, these factors can just form dimensionless frequency domain variables. Inspired by this, the present invention establishes a dimensionless mathematical model by substituting dimensionless parameters into the existing fourteen equation model.

[0059] The dimensionless parameters set include:

[0060]

[0061]

[0062]

[0063]

[0064]

[0065]

[0066] (2) Solve the transfer matrix of the dimensionless mathematical mo...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention aims to provide a transfer matrix calculation stability optimization method based on dimensionless analysis. The transfer matrix calculation stability optimization method comprises the following steps: substituting a fourteen-equation tubular beam model through a method of setting dimensionless parameters, and establishing a straight tube dimensionless model; expressing the fourteen-equation dimensionless model in the form of a matrix equation, then solving the matrix equation by utilizing a Laplace transformation method, and finally obtaining a frequency domain dimensionless transfer matrix model; introducing boundary conditions, external acting force and other definite solution conditions , calculating the pipeline dynamics problem, and drawing response curves of the torsional vibration velocity and the transverse vibration velocity ; obtaining the upper limit frequency and the maximum pipe length of stable calculation of the transfer matrix, carrying out segmentation processing on the pipeline exceeding the maximum pipe length, and eliminating the phenomenon of unstable calculation in a segmentation dimension expansion mode. According to the method, the optimization process does not cause great increase of the variable freedom degree number, and high calculation efficiency is ensured while the problem of unstable calculation is solved.

Description

technical field [0001] The invention relates to a transfer matrix calculation stability optimization method of an elastic structure. Background technique [0002] The fluid-solid coupling vibration problem of the pipeline system is called a "typical dynamic problem", which involves most of the problems in the fluid-solid coupling mechanics, and has a broad engineering background, especially the pipeline is easy to design and manufacture. This facilitates the coordination of theoretical research and experimental research. The commonly used methods in the study of fluid-structure coupling vibration problems in piping systems mainly include: transfer matrix method TMM (Transfer Matrix Method) in the frequency domain, characteristic line method MOC (Method Of Characteristics) in the time domain and finite element method FEM (Finite Element Method) and so on. When using TMM to calculate the fluid-solid coupling vibration problem of the pipeline system, the mathematical model of...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F30/17G06F17/16G06F111/10
CPCG06F17/16Y02T90/00
Inventor 柳贡民曹银行张文平张新玉明平剑曹贻鹏国杰赵晓臣
Owner HARBIN ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com