Quadruped robot single-leg trajectory tracking control method and system

A quadruped robot, trajectory tracking technology, applied in general control system, control/adjustment system, adaptive control, etc., to achieve the effect of improving trajectory tracking performance, high-precision trajectory tracking control, and improving performance

Pending Publication Date: 2021-08-06
QILU UNIV OF TECH
View PDF6 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] In order to solve the above problems, this disclosure aims at the single leg of the quadruped robot, and uses the excellent nonlinear approximation ability of the neural network to propose a quadruped robot single leg based on RBF (Radial Basis Function) neural network (NN, Neural Networks) compensation control. The leg trajectory tracking control method is used to compensate the influence of nonlinearity and error, improve the performance of the nonlinear control system of the qua

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Quadruped robot single-leg trajectory tracking control method and system
  • Quadruped robot single-leg trajectory tracking control method and system
  • Quadruped robot single-leg trajectory tracking control method and system

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0034] Example 1

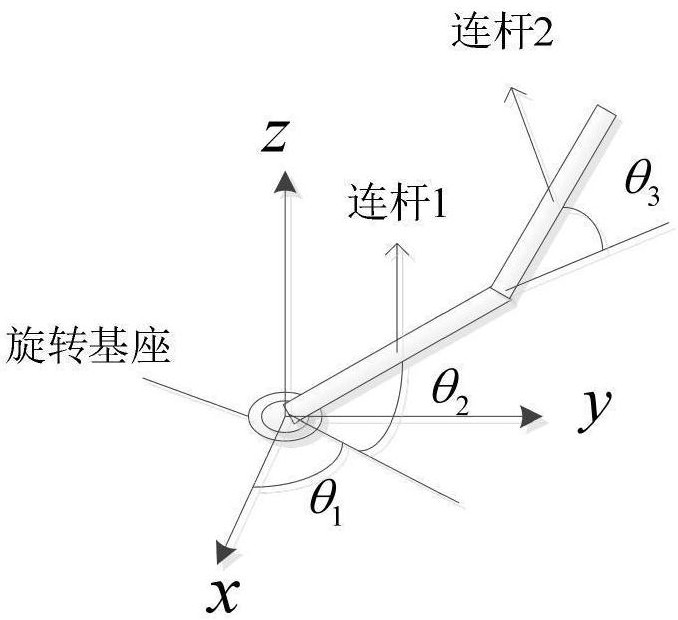
[0035] like figure 1 As shown, a four-legged robot single leg trajectory tracking control method, including:

[0036] Get the joint parameters of the quadruple robot;

[0037] Establish a single leg dynamics model according to joint parameters;

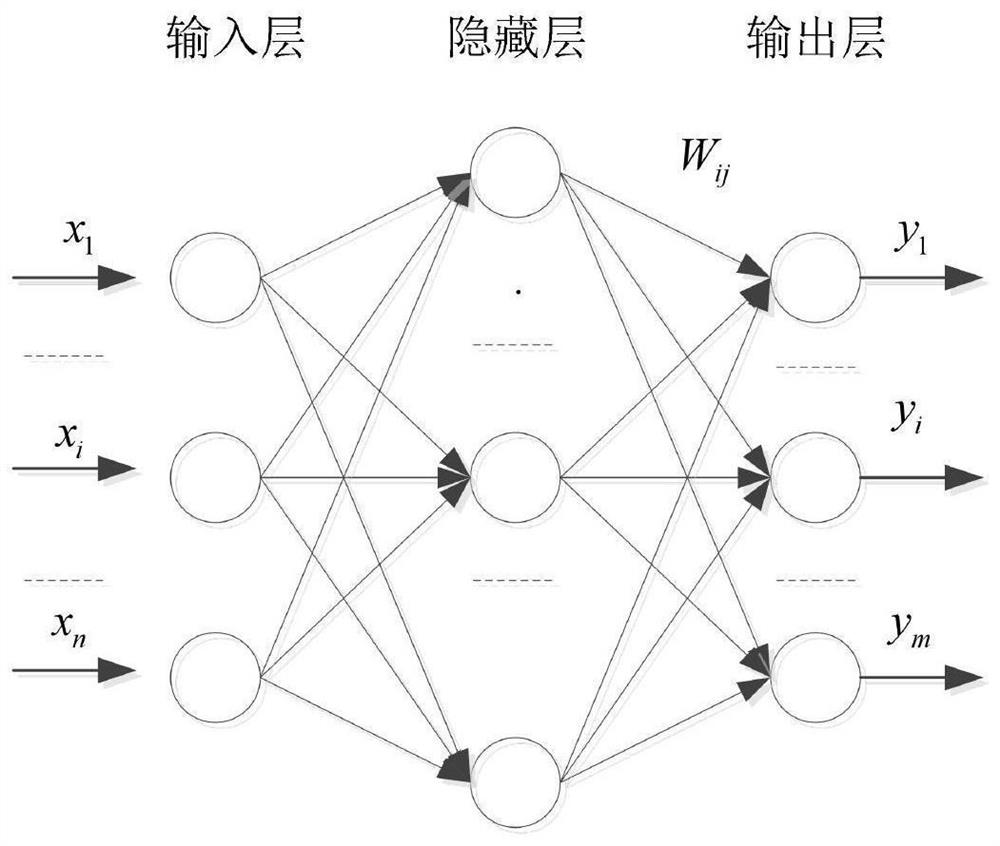
[0038] Based on disturbance and neural network to correct single leg dynamics model, construct a single leg dynamics model in the case of disturbance, and assume a reference trajectory;

[0039] Using a value-based function approximation method based on neural network learning, the optimal parameters of the reference trajectory are obtained, and the optimal control rate is obtained;

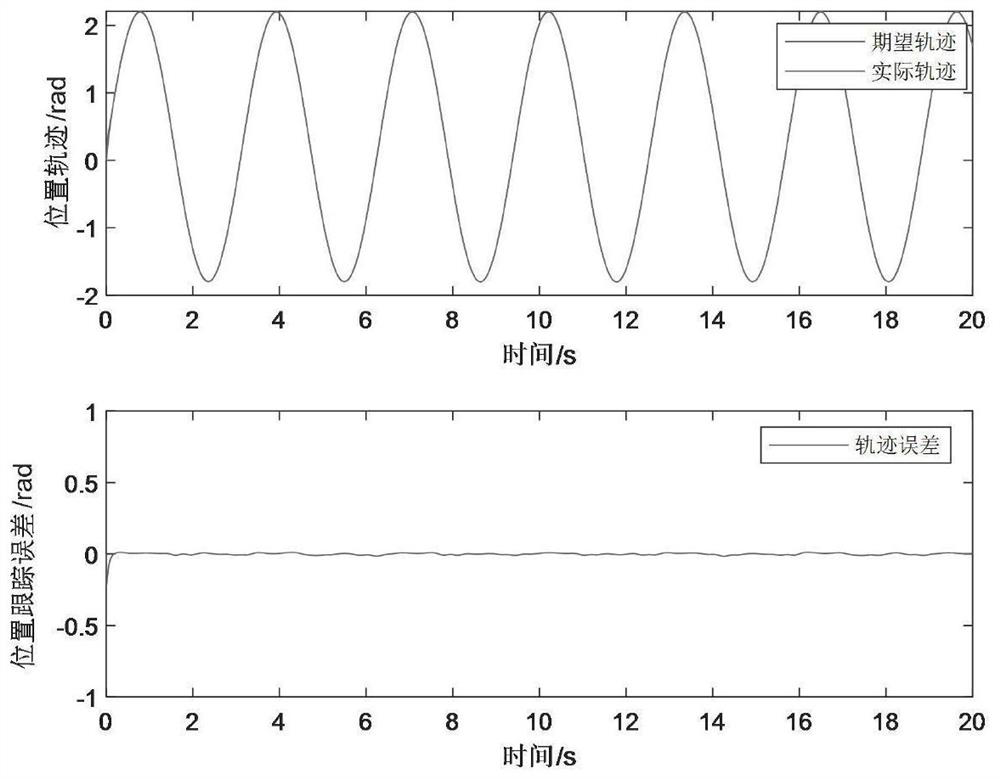
[0040] Based on the optimal control rate to realize the single leg trajectory tracking control of the quadruple robot.

[0041] Further, the joint parameters include joint position, speed, and acceleration vectors.

[0042] Further, according to the joint parameters, the one-leg dynamic model is established, and the control torque vector i...

Example Embodiment

[0117] Example 2

[0118] The present disclosure provides a four-legged single leg trajectory tracking controller, including:

[0119] The data acquisition module is configured to obtain joint parameters of the four-legged robot;

[0120] Single leg dynamics model establishment module is configured to establish a single leg dynamics model according to joint parameters;

[0121] The reference track establishment module is configured to correct the single leg dynamics model based on the disturbance and neural network, construct a single leg dynamics model in the case of disturbance, and assume the reference trajectory;

[0122] The control rate acquisition module is configured to obtain the optimal parameters of the reference trajectory using a value function based on neural network learning, and obtain the optimal control rate;

[0123] The tracking control module is configured to implement a single leg trajectory tracking control based on the optimal control rate.

[0124] Further,...

Example Embodiment

[0125] Example 3

[0126] The present disclosure provides a four-legged robot single leg trajectory tracking control system, which includes a four-foot robot single leg trajectory tracking controller as described above.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention provides a quadruped robot single-leg trajectory tracking control method and system. The quadruped robot single-leg trajectory tracking control method comprises the steps of obtaining joint parameters of a quadruped robot; establishing a single-leg dynamic model according to the joint parameters; correcting the single-leg dynamical model based on disturbance and a neural network, constructing a single-leg dynamical model under the condition of considering disturbance, and assuming a reference trajectory; obtaining an optimal parameter of the reference trajectory by using a value function approximation method based on neural network learning, and obtaining an optimal control rate; and achieving single-leg trajectory tracking control of the quadruped robot based on the optimal control rate. The method solves the problem of how to compensate the influence of nonlinearity and errors, improves the performance of a nonlinear control system of the quadruped robot, guarantees that the trajectory tracking error of the quadruped robot is gradually converged to zero, and achieves the high-precision trajectory tracking control of the quadruped robot.

Description

technical field [0001] The disclosure belongs to the technical field of robot control, and in particular relates to a single-leg trajectory tracking control method and system for a quadruped robot. Background technique [0002] The statements in this section merely provide background information related to the present disclosure and may not necessarily constitute prior art. [0003] Since the end of the last century, the research on robotics has been a research hotspot in scientific research institutions and technology companies at home and abroad. Footed bionic robots are one of the most challenging topics in robotics. Among them, quadruped robots are the most developed in the field of bionic robots. One of the fastest robot types, quadruped robots have the characteristics of high dynamic performance, strong adaptability to complex terrain, and strong anti-interference ability. Compared with wheeled robots, they are more flexible and have stronger passability and Adaptabil...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G05B13/04
CPCG05B13/042Y02P90/02
Inventor 梁启星李彬刘伟龙侯兰东李志杨雪李江娇高梦奇
Owner QILU UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap