Optical fiber nonlinear equalization method based on IPCA-DNN algorithm
An equalization method and nonlinear technology, applied in the field of optical fiber communication, can solve problems such as large computational complexity, high computational complexity, and difficulty in obtaining the global optimal solution, and achieve accurate prediction results
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0037] The present invention will be described in further detail below in conjunction with the accompanying drawings and specific embodiments. The technical scheme adopted in the present invention is:
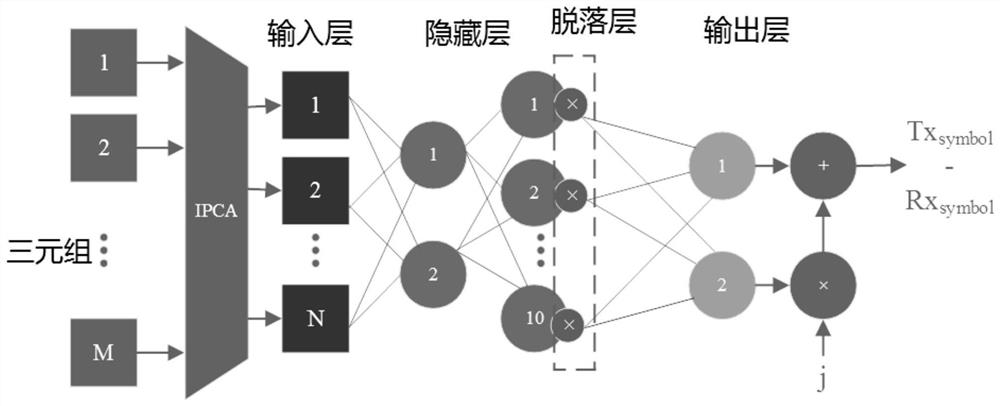
[0038] Firstly, the dispersion compensation module is used to compensate the linear damage of the transmission link, and then the triplet of intra-channel cross-phase modulation and intra-channel four-wave mixing is calculated to provide to the neural network. The triplet is trained by the neural network to generate a black-box model of the transmission link, and the nonlinear damage value of the model is obtained in the execution stage. figure 1 The NLC model based on IPCA-DNN algorithm is given, in which, in order to avoid neural network over-fitting, it is necessary to add a drop-off layer with a probability of 0.5 after the second hidden layer.
[0039] Experimental data needs to be obtained: constructing a long-distance optical transmission system of PDM-16QAM. At the tr...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com