Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

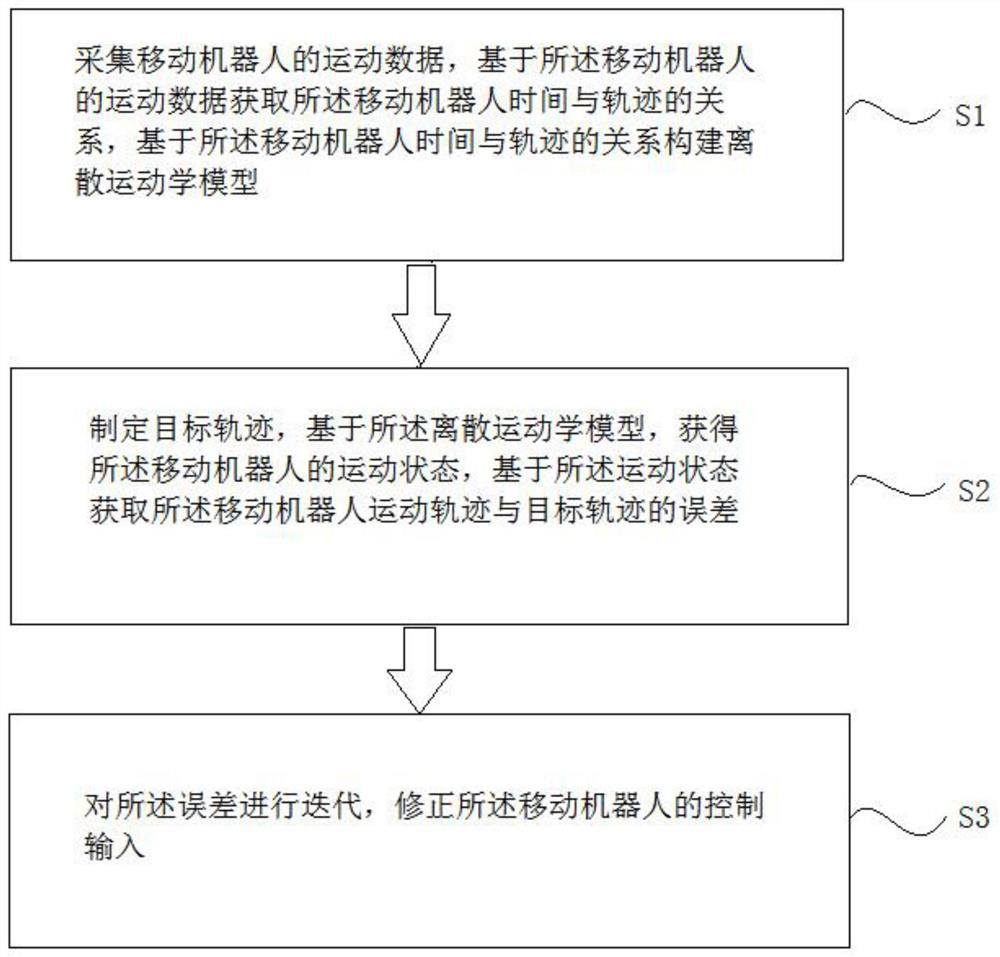
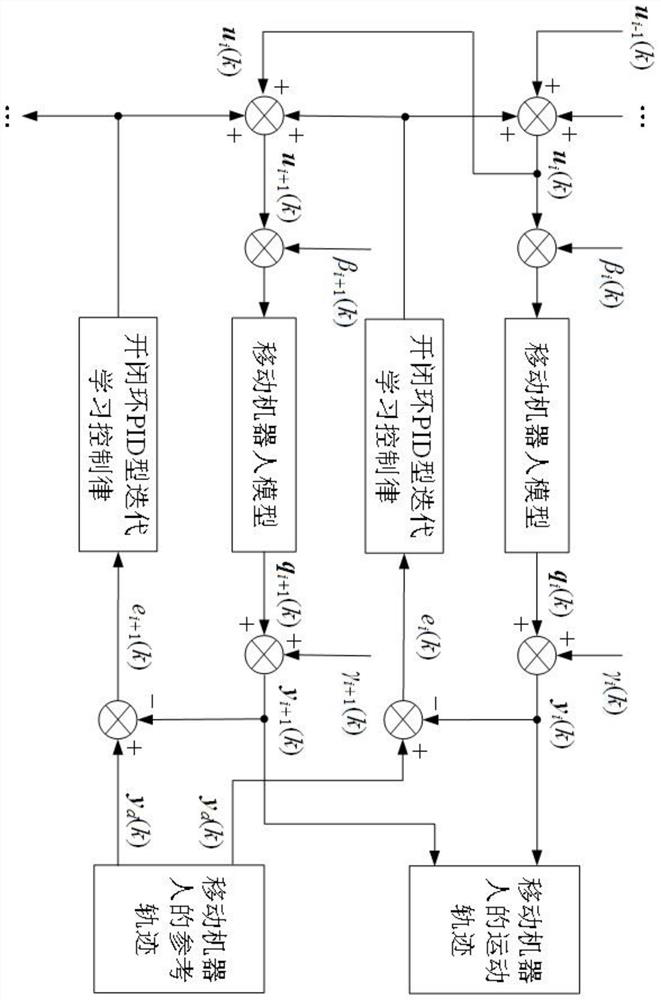
Robot trajectory tracking control method based on open-closed loop PID (Proportion Integration Differentiation) type iterative learning

An iterative learning and trajectory tracking technology, applied in two-dimensional position/channel control, non-electric variable control, control/regulation system, etc., to improve system tracking control performance, reduce external interference and noise effects, and improve tracking effect. Effect

Inactive Publication Date: 2021-09-03
BEIJING UNIV OF POSTS & TELECOMM
View PDF2 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Therefore, from the point of view of control, both methods have certain defects.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Robot trajectory tracking control method based on open-closed loop PID (Proportion Integration Differentiation) type iterative learning
  • Robot trajectory tracking control method based on open-closed loop PID (Proportion Integration Differentiation) type iterative learning
  • Robot trajectory tracking control method based on open-closed loop PID (Proportion Integration Differentiation) type iterative learning

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

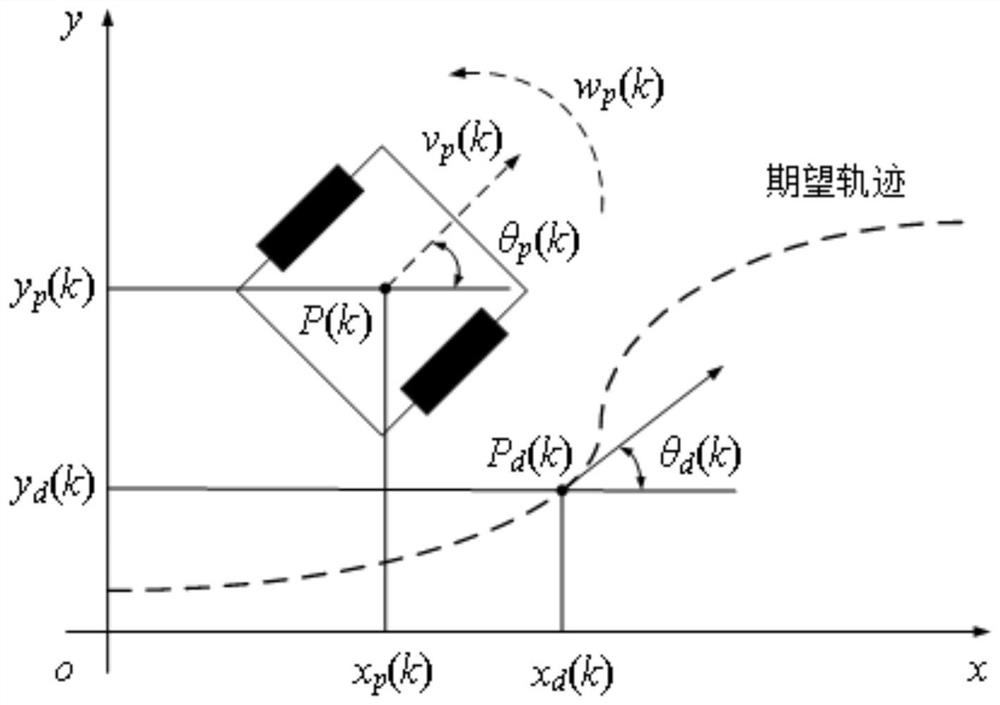
[0087]With reference to shown in Fig. 4-9, in order to verify the superiority of the open-closed-loop PID type iterative learning control law that the present invention proposes to mobile robot trajectory tracking, and (H.Wang, J.Dong, and Y.Wang, "Discrete PID-Type Iterative Learning Control for Mobile Robot," Journal of Control Science and Engineering, pp.1-7, 2016.) The trajectory tracking controller of the mobile robot designed by the PID-type iterative learning control law was experimentally compared. The mobile robot coordinates from the initial state P(0)=[1, 0, π / 2] T Track a circular trajectory with a radius of 1m, and the equation of the circular trajectory is P d =[x d (t),y d (t), θ d (t)] T =[cos(0.05πt), sin(0.05πt), 0.05πt+π / 2] T . The selected PID parameter is k p =0.02,k i =0.02,k d =0.01, the state interference term is β i (t)=0.001[sin(40πt)+0.05random(0,8), sin(40πt)+0.05random(0,8), sin(40πt)+0.05random(0,4)] T , the output measurement noise is ...

Embodiment 2

[0091] Referring to Figures 10-15, in order to further verify that the open-closed-loop PID-type iterative learning control law proposed by the present invention can be applied to mobile robots tracking other trajectories, here a cosine curve is selected as the tracking trajectory of the robot. And compared with the trajectory tracking controller of mobile robot designed by PID iterative learning control law. The mobile robot starts from the initial state P(0)=[0,1,0] T Tracking the cosine trajectory, the cosine trajectory equation is expressed as follows:

[0092] P d =[x d (t),y d (t), θ d (t)] T =[0.125t, cos(0.125t), -atan(sin(0.125t))] T

[0093] In the formula, t is the moving time of the robot, and the selected PID parameter is k p =0.02,k i =0.015,k d = 0.01. The values ​​of the state interference term and noise are the same as those in Embodiment 1.

[0094] Part of the motion picture of the cosine trajectory tracking of the mobile robot executing the open...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a robot trajectory tracking control method based on open-closed loop PID type iterative learning, and the method comprises the following steps: S1, collecting the motion data of a mobile robot, and obtaining the relation between the time and trajectory of the mobile robot based on the motion data of the mobile robot, constructing a discrete kinematics model based on the relation between the time and the trajectory of the mobile robot; S2, making a target track, obtaining a motion state of the mobile robot based on the discrete kinematics model, and obtaining an error between the motion track of the mobile robot and the target track based on the motion state; and S3, iterating the error, and correcting the control input of the mobile robot. According to the method, an open-loop iterative learning control law and a closed-loop iterative learning control law can be combined, an output trajectory can be quickly realized to track a target trajectory within finite time, meanwhile, the requirements of a robot system for tracking precision and anti-interference performance are met, and the system tracking control performance of the robot is improved.

Description

technical field [0001] The invention relates to the field of trajectory tracking control of mobile robots, in particular to a robot trajectory tracking control method based on open-closed-loop PID iterative learning. Background technique [0002] Mobile robots have time-varying, strong coupling, and nonlinear dynamic characteristics. Due to inaccurate measurement and modeling, coupled with load changes and the influence of external disturbances, it is actually impossible to obtain an accurate and complete mobile robot motion model. A well-designed controller is an important prerequisite to ensure that the robot can track the trajectory, so it is of great significance to further improve the control accuracy and convergence speed of the trajectory tracking of the mobile robot. [0003] At present, many methods have been used to solve the trajectory tracking problem of mobile robots, such as optimal control, backstepping control, sliding mode control, fuzzy control, neural netw...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05D1/02
CPCG05D1/0223G05D1/0221G05D1/0276
Inventor 刘晓平黎星华顾恺琦田智予张承耀
Owner BEIJING UNIV OF POSTS & TELECOMM
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com