BERT model training method and system based on multiplier alternating direction method
An alternate direction method and model training technology, applied in the field of BERT model training methods and systems based on the multiplier alternate direction method, can solve problems such as large memory space, consumption, and large memory space consumption, so as to improve efficiency and accuracy, improve Training efficiency, the effect of reducing the amount of calculation
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0057] The present invention will be further described below with reference to the accompanying drawings and specific preferred embodiments, but the protection scope of the present invention is not limited thereby.
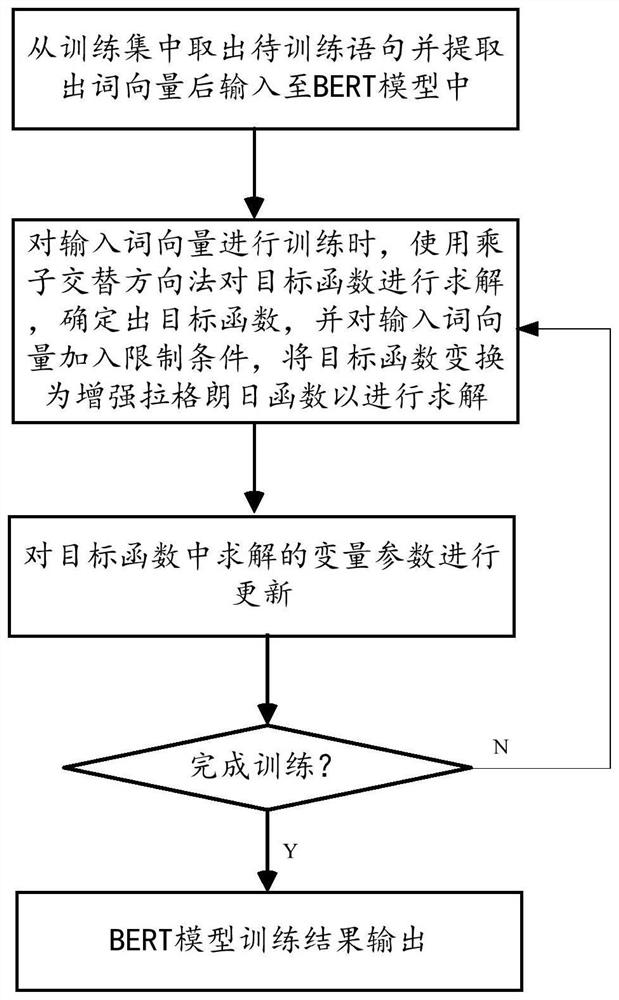
[0058] like figure 1 As shown, the steps of the BERT model training method based on the multiplier alternating direction method in this embodiment include:
[0059] Step S1. Data input: take out the sentence to be trained from the training set and extract the word vector and input it into the BERT model;
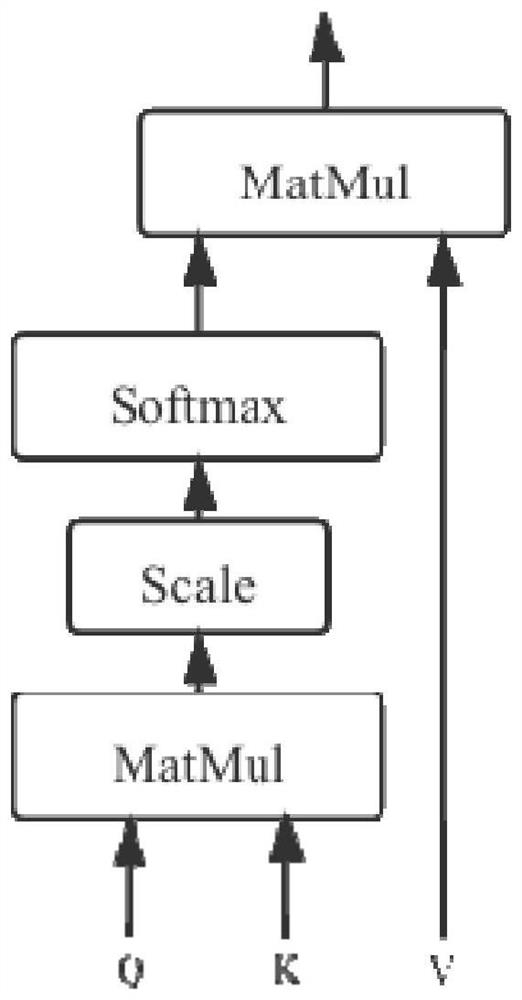
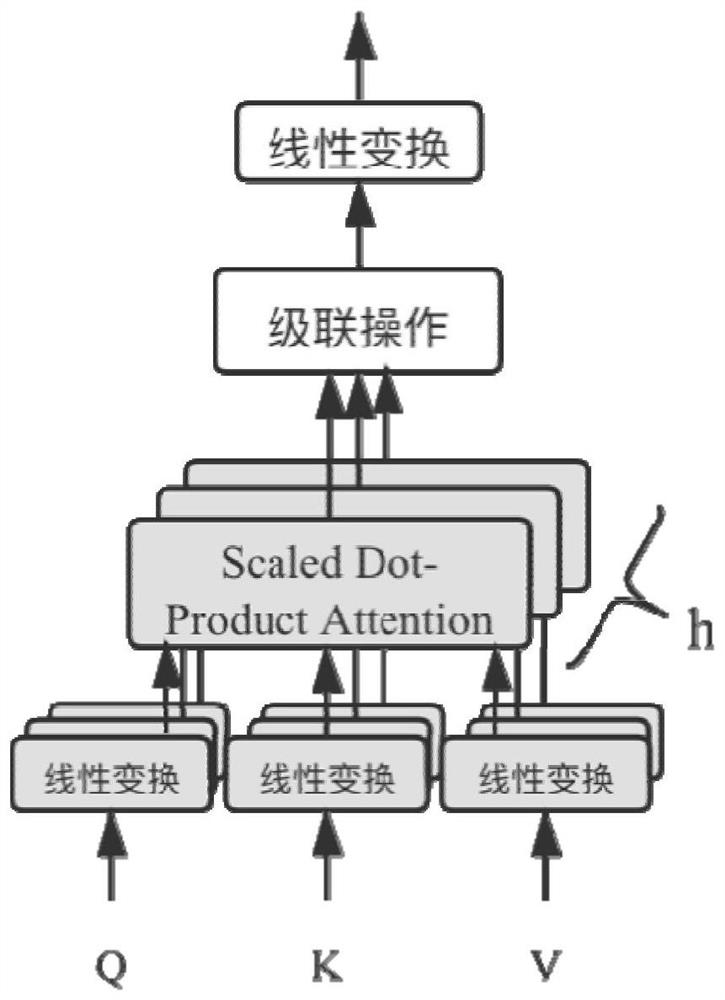
[0060] Step S2. Multiplier Alternate Direction Method Solution: When the BERT model trains the input word vector, the multiplier alternate direction method is used to solve the objective function, wherein the representation of the BERT model by the Encoder module in the Transformer model is used to determine the objective function, Constraints are added to the input word vector, and the enhanced Lagrangian algorithm is used to transform the objective function i...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com