Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

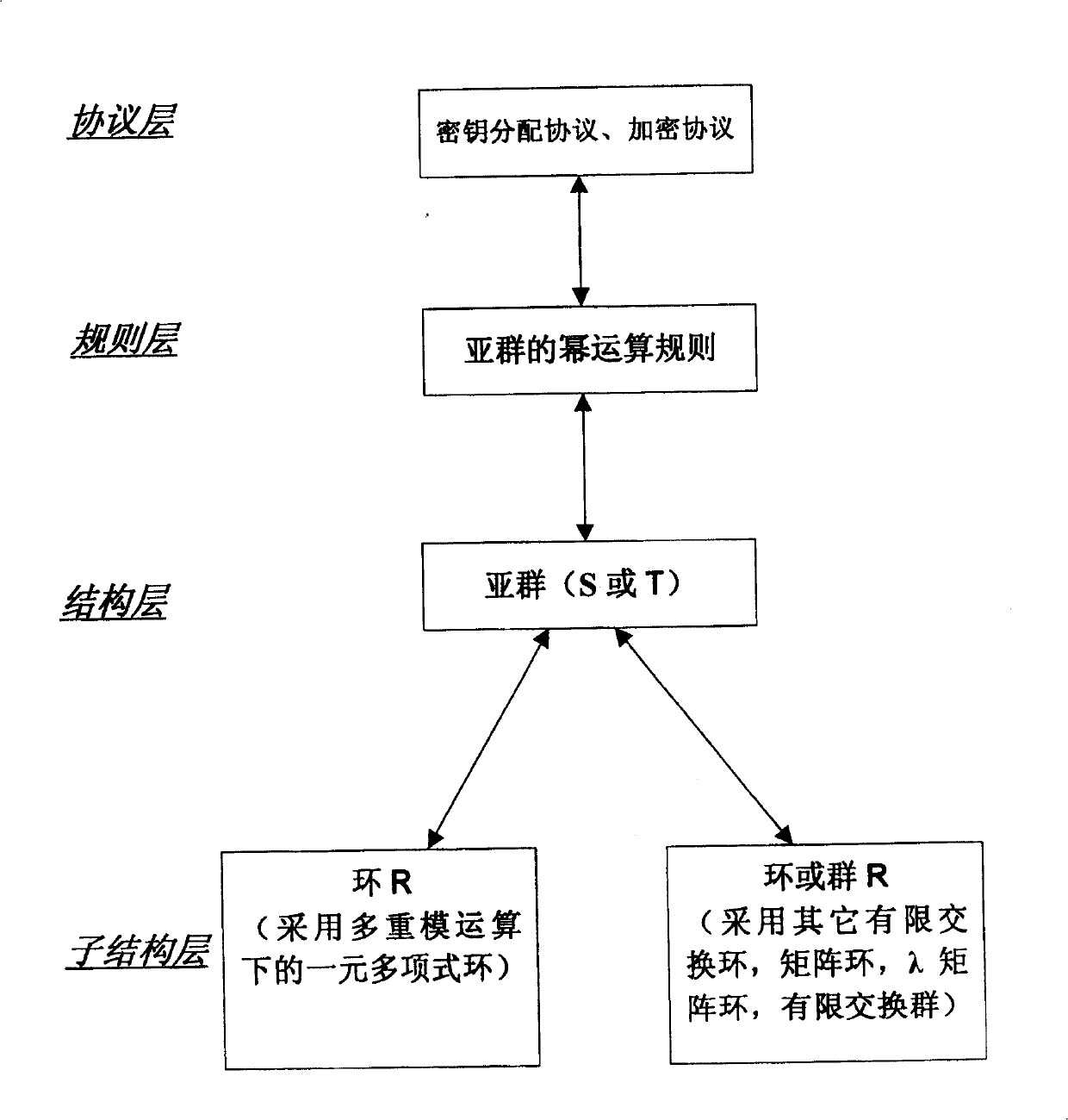
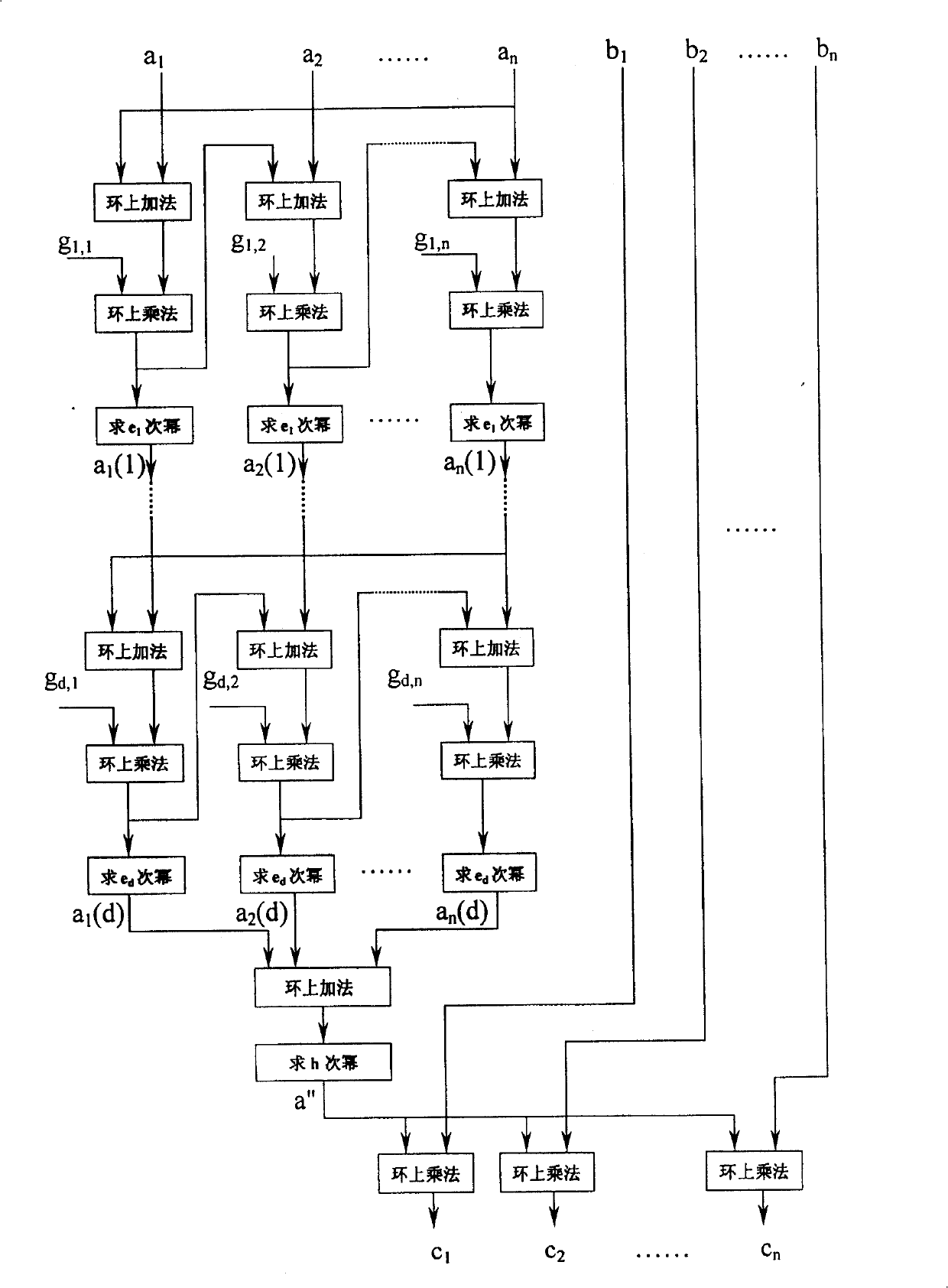
Method of key allocation as cell as encryption and decryption protocols based on discrete logarithm problem on subcluster

A discrete logarithm problem and key distribution technology, which is applied in the field of cryptography and information security, and can solve the problems of increasing the difficulty of cryptanalysis, and the lack of key distribution and encryption and decryption methods.

Inactive Publication Date: 2008-11-05
管海明
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Secondly, the research on subgroups in contemporary mathematics is very immature. Due to long-term lack of attention, there are few literatures, and a large number of existing theories and results of group theory cannot be directly extended to subgroups, which further increases the scope of cryptanalysis. Difficulty
In view of the blank status of subgroup research, there has never been a subgroup-based key distribution and encryption and decryption method in the prior art

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method of key allocation as cell as encryption and decryption protocols based on discrete logarithm problem on subcluster
  • Method of key allocation as cell as encryption and decryption protocols based on discrete logarithm problem on subcluster
  • Method of key allocation as cell as encryption and decryption protocols based on discrete logarithm problem on subcluster

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0225] Embodiment 1, using a one-variable polynomial ring R under multi-modular operations to construct a zero-factor subgroup S and implement a key distribution protocol

[0226] A simple example of using two-level nonlinear algebraic expansion, using R[v(y)] as R is as follows:

[0227] Set the parameters: n=2, d=2, h=3, e 1 =e 2 =2, s=3, k=2, m=30967 (the prime decomposition of m is 173×179)

[0228] u(x)=x 3 +10331x 2 +29191x+15575

[0229] v(y)=y 2 +(22823x 2 +23508x+17188)y+(25335x 2 +15462x+8727)

[0230] The coefficients used in the first layer of nonlinear transformation are

[0231] g 1，1 =(4973x 2 +23767x+18329)y+(23747x 2 +15427x+1693)

[0232] g 1，2 =(6007x 2 +9721x+24439)y+(8543x 2 +2267x+28909)

[0233] The coefficients used in the second layer nonlinear transformation are

[0234] g 2，1=(1373x 2 +23053x+13331)y+(22273x 2 +17x+10771)

[0235] g 2，2 =(3989x 2 +24239x+10459)y+(19471x 2 +30631x+2837)

[0236] After constructing a subgroup with zero factors, the followi...

Embodiment 2

[0254] Example 2, using the remaining ring-like Z m The matrix ring on is constructed with zero factor subgroup S

[0255] Set parameters: n=2, h=5, modulus m=30967 (prime decomposition is 173×179), matrix dimension s=2, coefficient: g 1 = 22908, g 2 =25701, base A={A 1 , A 2 }, respectively

[0256] A 1 = {14419, 11240,

[0257] 19910, 18552}

[0258] A 2 = {21901, 19947,

[0259] 30530, 5692}

[0260] Let L a = 13177, L b = 8754. Using the most basic exponentiation rule, the experimental results of interactive key distribution are as follows:

[0261] Party A calculates A's L a Power: B a ={B a1 , B a2 }, respectively

[0262] B a1 ={17788,5679,

[0263] 18961, 7429}

[0264] B a2 = {4356, 6364,

[0265] 30955, 16037}

[0266] Party B calculates A's L b Power: B b ={B b1 , B b2 }, respectively

[0267] B b1 = {5000, 4790,

[0268] 18803, 14817}

[0269] B b2 = {5063, 20666,

[0270] 28003, 30615}

[0271] Party A calculates B b L a Power: K a ={K a1 , K a2 }, respectively

[027...

Embodiment 3

[0282] Example 3, using finite field F p Construct zero-factor subgroup T

[0283] Let n=4, h=2, e=3, F p The characteristic of P=32749, the base A={6469,21211,18047,13859}, the coefficient g 0 = 10739, g 1 = 30403, g 2 = 9479, g 3 = 9461, g 4 =32189, using the most basic exponentiation rule, the experimental results of interactive key distribution are as follows:

[0284] Let L a = 51761, L b =45233.

[0285] Party A calculates A's L a Power: B a = {25044, 9122, 1891, 20748};

[0286] Party B calculates A's L b Power: B b = {18605, 23601, 11904, 9278};

[0287] Party A calculates B b L a Power: K a = {25087, 32180, 20024, 15618};

[0288] Party B calculates B a L b Power: K b = {25087, 32180, 20024, 15618}.

[0289] It can be seen that K a And K b The calculated results are the same.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention is applicable to cipher key allocation and information encryption in public channel. A class of subcluster is constructed to meet following conditions: close, non-combination, non-commutation, non-identity element, non-inverse element, dissatisfying distributive law of general addition, and only satisfying exponential commutative law of exponent operation. Rule of exponent operation is constructed. Using constructed subcluster and law of exponent operation creates cipher key shared by both parties. The invention first discloses and realizes a class of subcluster possessing special property. Based on law of exponent operation of the subcluster, very complex iteration function relevant to exponential sequence is constructed, making traditional analytical method and concept, which seeks discrete logarithm by using cyclophysis, become no sense. Breaking cipher code is resolved into searching binary tree. Thus, system of public key cryptography gains substantive improvement.

Description

Technical field [0001] The present invention belongs to the field of cryptographic technology and information security technology. It is a method of using difficult problems in mathematics, specifically, using the difficulty of solving discrete logarithms on subgroups to implement key distribution protocols, as well as encryption and decryption Protocol method. Background technique [0002] Cryptography is a science and technology for studying encryption and decryption transformation. Under normal circumstances, people call the understandable text as plaintext; the incomprehensible text transformed into plaintext is called ciphertext. The process of transforming plaintext into ciphertext is called encryption; the reverse process, that is, the process of transforming ciphertext into plaintext is called decryption. The mutual transformation between plaintext and ciphertext is a reversible transformation, and there is only a unique and error-free reversible transformation. For the d...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/14H04L9/28H04L9/08
CPCH04L9/0841
Inventor 管海明
Owner 管海明
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com