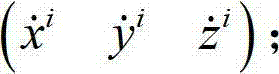Quick integrated navigation method based on Carlson filtering algorithm for reducing dimensionality
A filtering algorithm and integrated navigation technology, applied in the field of satellite navigation and inertial navigation, can solve the problems of easy divergence of data fusion filters, large amount of data, and difficult hardware implementation
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0046] Describe the present invention below in conjunction with specific embodiment:
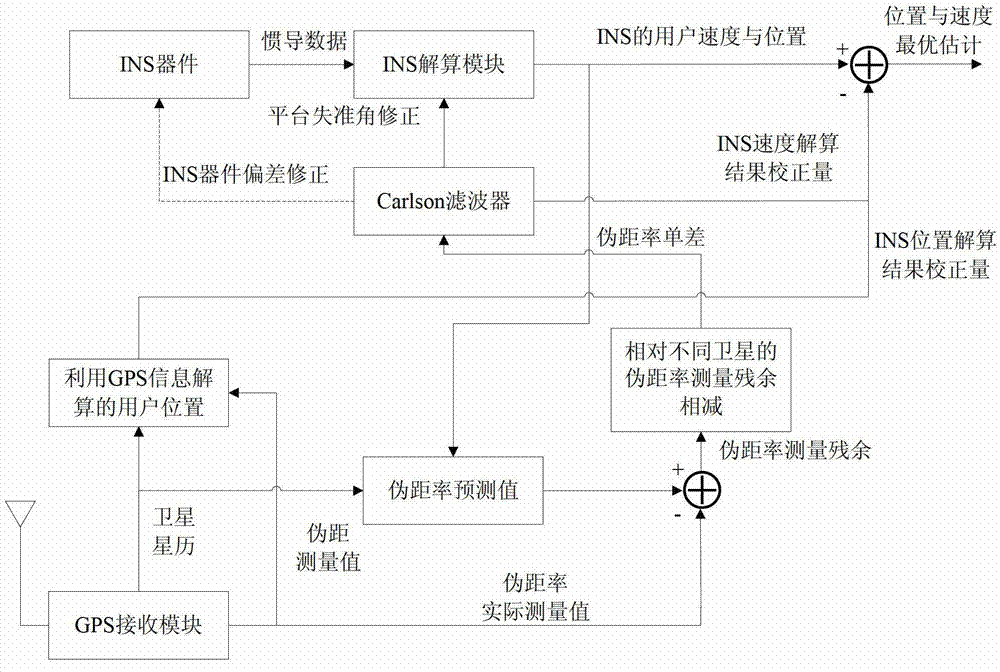
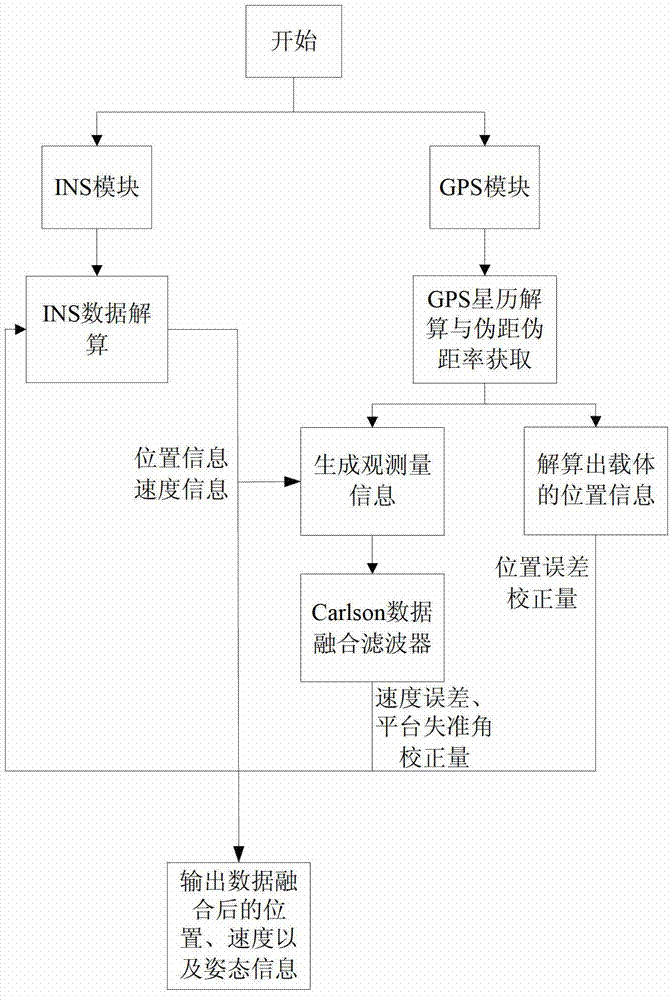
[0047] The specific implementation scheme of the data fusion method of this embodiment is shown in the figure figure 1 As shown, the user uses the collected raw data of the INS device to calculate the INS navigation data, calculate the attitude information, position information and speed information of the carrier, count the INS calculation module, and perform a combined navigation every 5 times Data Fusion. Using the data fusion method based on Carlson filter with dimensionality reduction, the data fusion of GPS navigation system and INS navigation system is realized. The specific steps are as follows:
[0048] Step 1: Using the satellite position information and pseudo-range information obtained by the GPS receiver, use the above information to calculate the current user position (x y z) and user speed (v x v y v z ); pass the value to the INS module to update the location informatio...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com