Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

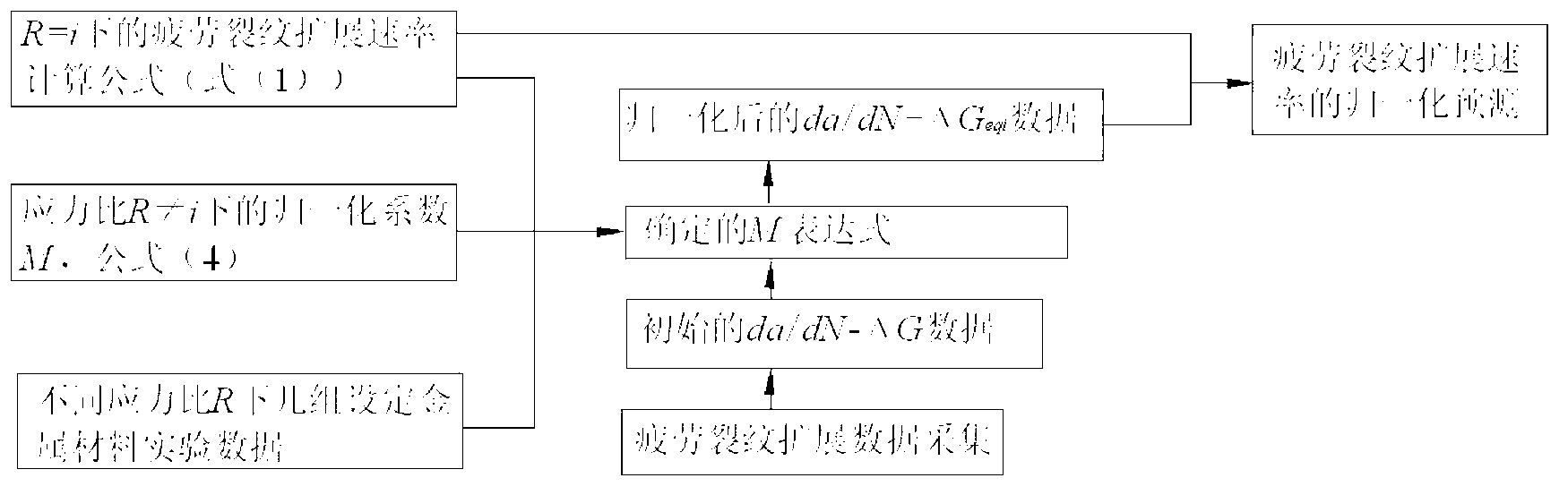
Fatigue crack spreading rate normalization forecasting method

A technology of fatigue crack growth and prediction method, which is applied in the field of normalized prediction of fatigue crack growth rate based on energy release rate, can solve problems such as lack of good unity and difficulty in accurate fatigue life prediction, and achieve simple form, Facilitate engineering application and reduce workload

Active Publication Date: 2013-09-18
HEFEI GENERAL MACHINERY RES INST
View PDF7 Cites 21 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Regarding the influence of the stress ratio R, most of the current research work is based on the modified Paris formula for I-type fatigue crack growth, such as the early Forman formula (1967), Elber formula (1970), Walker formula (1970), and recent The calculation models of Kujawski et al. and Huang et al. (2007) in recent years; these correction formulas all use the stress intensity factor amplitude ΔK as the control parameter, and most of them have some shortcomings, such as the experimental undetermined constants related to their materials vary with different stress ratios The variation, or the correction factor related to the stress ratio is not well unified for different materials, these situations will bring difficulties to accurate fatigue life prediction under variable amplitude loading

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fatigue crack spreading rate normalization forecasting method
  • Fatigue crack spreading rate normalization forecasting method
  • Fatigue crack spreading rate normalization forecasting method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0045] For the normalized prediction method of 4340 steel type I fatigue crack growth rate, the stress ratio is normalized to R=0, including the following steps:

[0046] First, establish a normalized prediction model for the fatigue crack growth rate

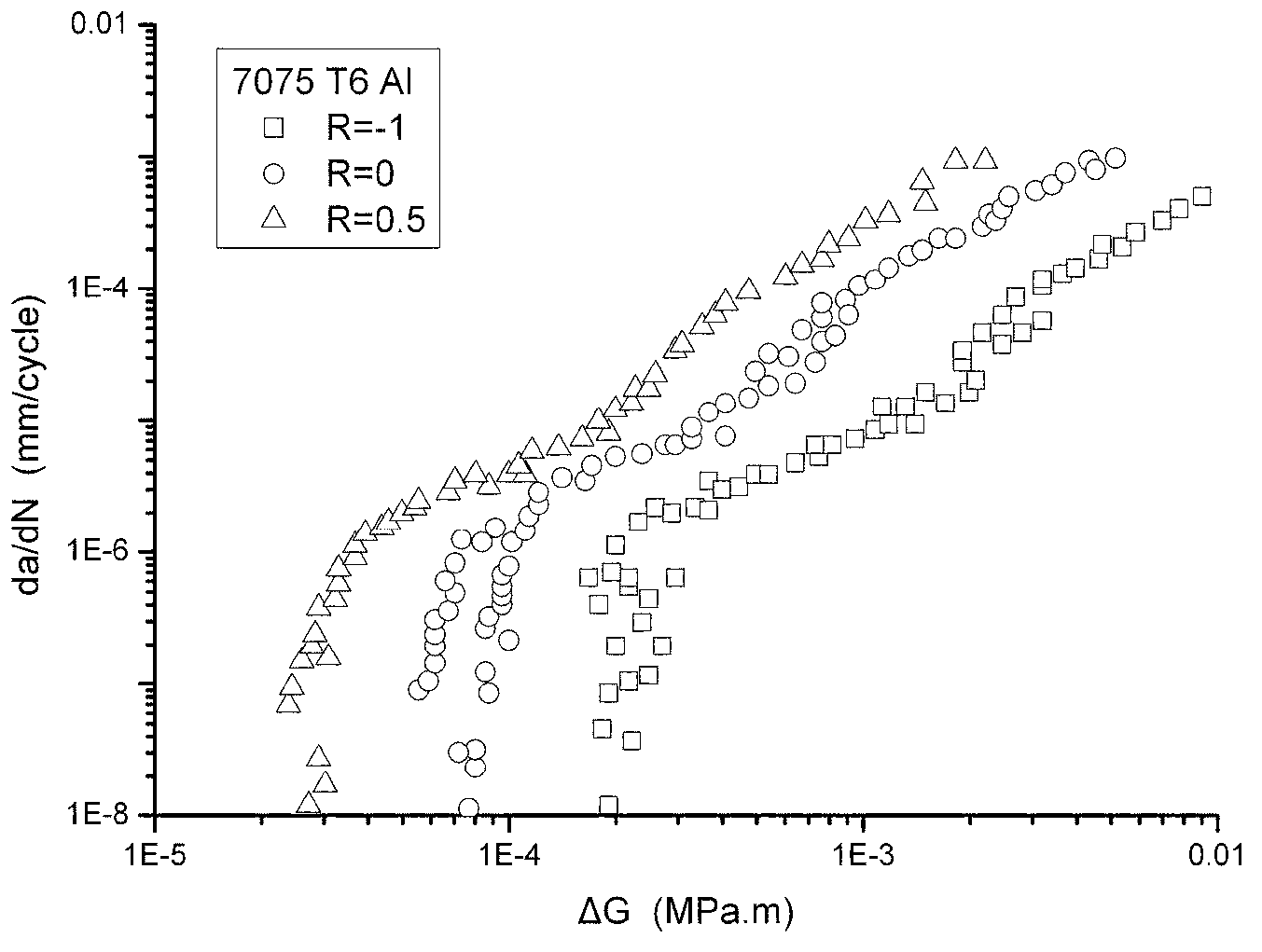
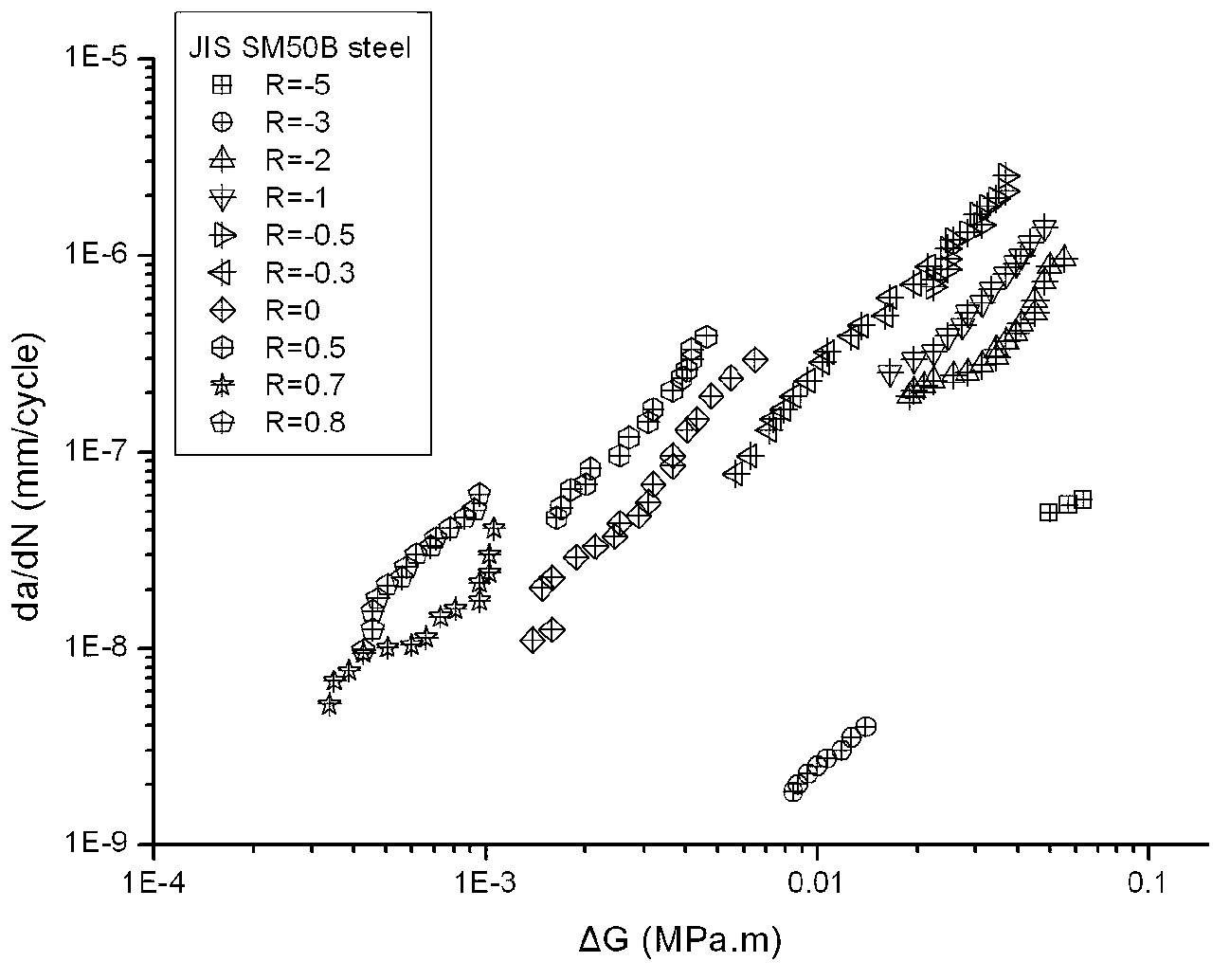
[0047] ① Plot the lg(da / dN)-lg(ΔG) data plot. Among them, 7075-T6 aluminum, stress ratio R=-1, 0 and 0.5 (see Figure 2 (a)); JIS SM50B steel, stress ratio R=-5, -3, -2, -1, -0.5, -0.3 , 0, 0.5, 0.7 and 0.8 (see Figure 2(b)); 2024-T351 aluminum (type1), the stress ratios are R=-1, 0, 0.1 and 0.3 (see Figure 3(a)); T351 aluminum (type2), stress ratio R=-2, -1, -0.5, 0, 0.1, 0.3, 0.5 (see Figure 3 (b)).

[0048] ②For the test data of R=0, the material constants obtained by fitting the above formula (1) through the least square method are: 7075-T6 aluminum, B=1.3115, m=1.3518, G th0 =6.29×10 -5MPam; JIS SM50B steel, B=0.0020, m=1.7236, G th0 =1.38×10 -3 MPam; 2024-T351 aluminum (type1), B=0.0003, m=1.1766, G th0 =5.55×10 ...

Embodiment 2

[0059] For the type III fatigue crack growth rate of 18G2A steel, the fatigue crack growth rate normalization prediction method based on the energy release rate normalizes the stress ratio to R=0, including the following steps:

[0060] First, draw the lg(da / dN)-lg(ΔG) fatigue crack growth rate data of 18G2A steel under the stress ratio R=-1, -0.5 and 0 on the log-logarithmic coordinates, see Figure 6 (a);

[0061] Second, the fatigue crack growth data under different stress ratios R is equivalent to R=0 using formula (7), and the stress ratio normalization coefficient M is equal to 0.2888 (R=-1), 0.4836 (R=-0.5) , the data distribution after equivalent is shown in Figure 6(b);

[0062] Third, the fatigue crack growth rate calculation formula based on the energy release rate (formula (1)), the material constant B=4×10 -5 , m=1.3170, the energy release rate change amplitude threshold ΔG th0 =1.0×10 -3 Mpam, the prediction curve of fatigue crack growth rate is obtained from t...

Embodiment 3

[0064] For the I-III fatigue crack growth rate of 18G2A steel, the fatigue crack growth rate normalization prediction method based on the energy release rate normalizes the stress ratio to R=0, including the following steps:

[0065] First, draw the lg(da / dN)-lg(ΔG) fatigue crack growth rate data of 18G2A steel under the stress ratio R=-1, -0.5 and 0 on the log-logarithmic coordinates, see Figure 7(a);

[0066] Second, the fatigue crack growth data under different stress ratios R is equivalent to R=0 using formula (7), and the stress ratio normalization coefficient M is equal to 0.2888 (R=-1), 0.4836 (R=-0.5) , the equivalent data distribution is shown in Figure 7(b);

[0067] Third, the fatigue crack growth rate calculation formula based on the energy release rate (formula (1)), the material constant B=4×10 -6 , m=1.1846, the energy release rate change amplitude threshold ΔG th0 =1.0×10 -3 Mpam, the prediction curve of fatigue crack growth rate is obtained from the data un...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to the field of forecast of a fatigue crack spreading rate of a material, and in particular relates to a fatigue crack spreading rate normalization forecasting method based on the energy release rate. The method comprises the following steps of: drawing a data map for setting a metal material to be under different stress ratios; constructing a fatigue crack spreading rate calculation formula for the metal material under the stress ratio of R:i of 1:1, FORMULA, and expressing the formula as a function; determining experiment constants and curves of the expression under the stress ratio of R:i of 1:1; constructing normalization method expressions of experiment data under different stress ratios that R is not equal to i, and obtaining the normalization method expressions, FORMULA; determining the value Alpha and a math expression Alpha=f(R), and determining an expression of a stress ratio normalization coefficient M and an expression of a data normalization method; and forecasting normalized data through the fatigue crack spreading rate formula under the determined stress ratio of R:i of 1:1. The method has the characteristics of simplicity, wide application range and the like and is favorable for engineering application.

Description

technical field [0001] The invention relates to the field of prediction of material fatigue crack growth rate, in particular to a normalized prediction method of fatigue crack growth rate based on energy release rate. Background technique [0002] Fatigue damage is one of the main failure modes of engineering structures under alternating loads. Studying the fatigue crack growth rate under different stress ratios is of great significance for evaluating the remaining life of engineering structures and determining their maintenance intervals. [0003] The crack growth rate is related to the change amplitude of the corresponding type of stress intensity factor. The formula for calculating the composite fatigue crack growth rate is its general form. At present, the effective stress intensity factor amplitude ΔK is mainly used in the literature eff Or use energy (such as ΔG, ΔJ, strain energy density factor amplitude ΔS, etc.) as the control parameter. Regarding the influence of ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01N3/00G06F17/00
Inventor 陈学东吴乔国范志超聂德福
Owner HEFEI GENERAL MACHINERY RES INST
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com