Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

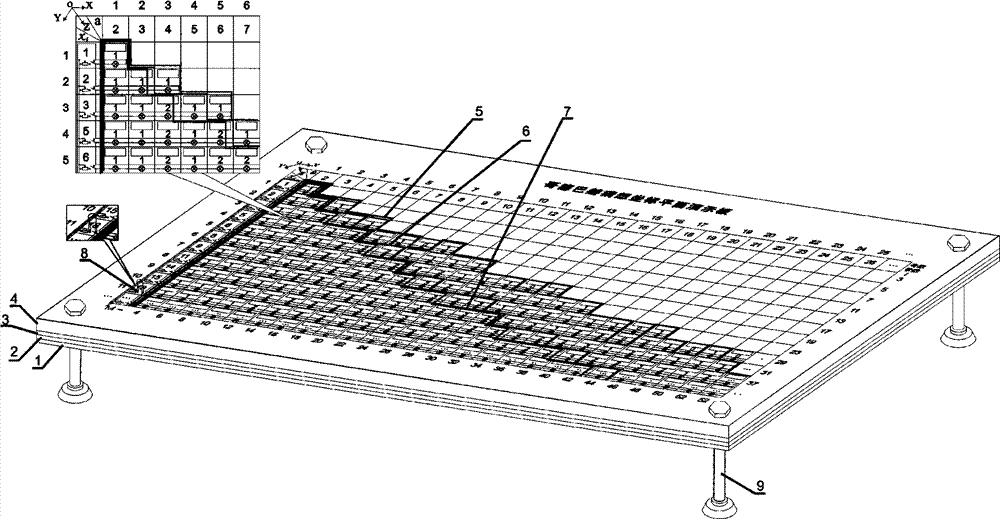
Goldbach conjecture proving coordinate plane demonstrator

A technology of Goldbach's conjecture and coordinate plane, which is applied to instruments, educational tools, teaching models, etc.

Active Publication Date: 2014-01-29
李中平
View PDF8 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The present invention aims to solve the problem that the prior art cannot apply the mathematical model demonstrating Goldbach's conjecture to carry out the activities of teaching Goldbach's conjecture in primary and secondary schools, and to solve the problem that mathematicians cannot apply existing mathematical concepts to finally complete the Goldbach's conjecture in terms of theory and method. Strictly prove the technical issues to provide a Goldbach conjecture proof coordinate plane demonstrator that is intuitive and accurate, has a wide range of applications, and is reliable in scientific principles and methods, and is easy for readers to recognize, understand and apply

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Goldbach conjecture proving coordinate plane demonstrator
  • Goldbach conjecture proving coordinate plane demonstrator
  • Goldbach conjecture proving coordinate plane demonstrator

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1 1

[0131] Embodiment 1 An algorithm proof method

[0132] To prove Goldbach's conjecture with an arithmetic proof, the formula M=2a+2=2(x i +x j )+2=(2x i +1)+(2x j +1)=X i +X j ≥6,X i ≤X j , starting from the positive even number 6, write only one formula for each even number, and the proof process and conclusion obtained in turn are as follows:

[0133] From Goldbach's 2=1+1, 6=2x2+2=2x(1+1)+2=(2×1+1)+(2×1+1)=3+3;

[0134] From Goldbach's 3=1+2, 8=2x3+2=2x(1+2)+2=(2×1+1)+(2x2+1)=3+5;

[0135] From Goldbach 4=1+3, 10=2x4+2=2x(1+3)+2=(2×1+1)+(2×3+1)=3+7;... ....

Embodiment 2

[0136] Embodiment 2 Multiple arithmetic proof methods

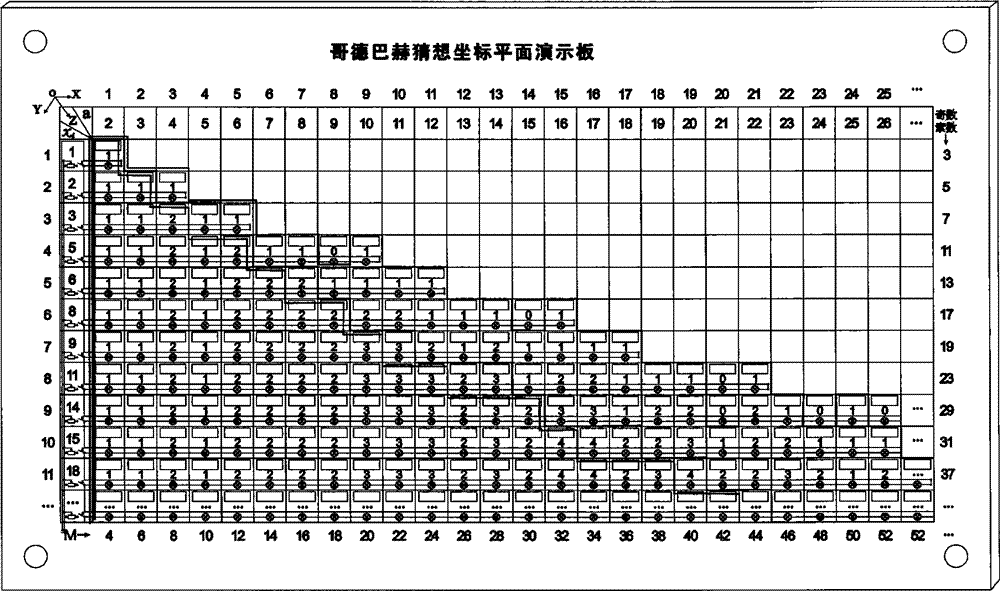
[0137] To prove Goldbach's conjecture with multiple arithmetic proofs, the formula M=2a+2=2(x i +x j )+2=(2x i +1)+(2x j +1)=X i +X j ≥6,X i ≤X j , to prove Goldbach's conjecture, for positive even numbers greater than 4, the proofs can be written as multiple formulas. For example, if Figure 12 As shown, when x=22, Goldbach's 23=2+21=3+20=5+18=8+15=9+14, the even number 48 greater than 5 must be written as the addition of two odd prime numbers The 5 solutions are:

[0138] The first solution is: 48=2x23+2=2x(2+21)+2=(2x2+1)+(2x21+1)=5+43;

[0139] The second solution is: 48=2x23+2=2x(3+20)+2=(2x3+1)+(2×20+1)=7+41;

[0140] The third solution is: 48=2x23+2=2x(5+18)+2=(2x5+1)+(2×18+1)=11+37;

[0141] The fourth solution is: 48=2x23+2=2x(8+15)+2=(2x8+1)+(2×15+1)=17+37;

[0142] The fifth solution is: 48=2x23+2=2x(9+14)+2=(2x9+1)+(2×14+1)=19+29;.......

Embodiment 3

[0143] Example 3 Applying the dividing line to determine the scope of proof

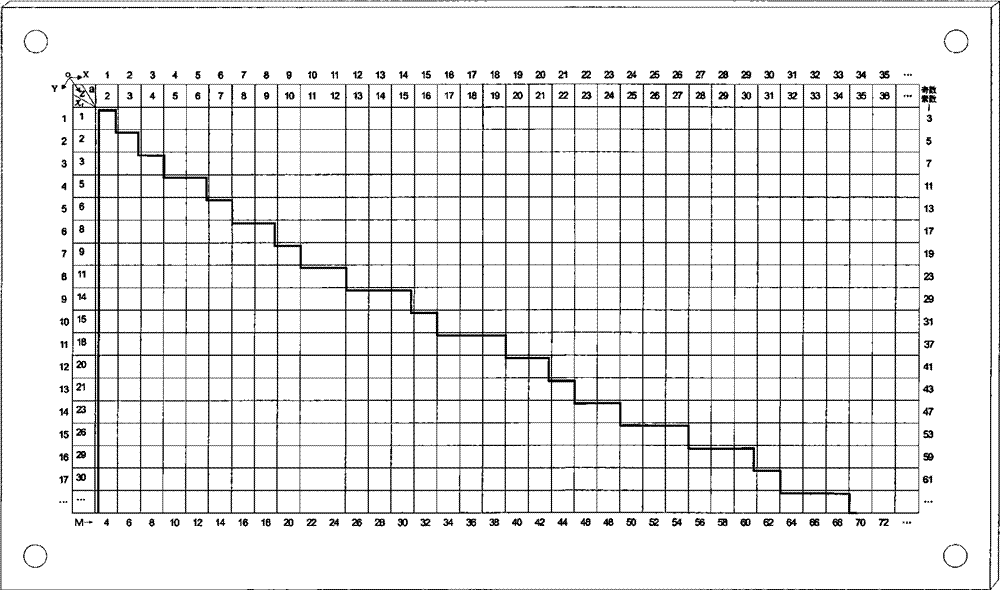
[0144] The demonstration of the present invention compares and distinguishes the dividing line of the proof of the double base theorem and the dividing line of the proof of an arithmetic formula, and judges and proves the valid scope of Goldbach's conjecture, which is convenient for practical application.

[0145] Apply odd prime base number columns 1, 2, 3, 5, 6 to determine x n=6, in "Goldbach's Conjecture Coordinate Plane Demonstrator", looking down at the 6th row where the odd prime number base 6 in the first column of the table is located, it is known to apply the double-basis theorem to prove that the boundary line can be in the range of the closed interval [2, 7] Within, complete the summation of Goldbach bases 2, 3, 4, 5, 6, 7, prove that Goldbach’s conjecture is established on the closed interval [6, 16], find the solution of each even number, the number is the largest, And it is at least 1...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to the fields of educational technology and studies in mathematical sciences, in particular to a Goldbach conjecture proving coordinate plane demonstrator, aiming to solve the technical problems that no instruments and models are provided for school teaching of Goldbach conjecture, proving of the Goldbach conjecture cannot be solved in the prior art and the like. The Goldbach conjecture proving coordinate plane demonstrator comprises a coordinate plane grid board (1), a coordinate-plane integrated circuit board (2), an odd-prime base addition equation number vertical-coordinate board (3), an odd-prime base addition equation prism bottom slot board (4), a one-equation proving boundary (5), a maximum-equation proving boundary (6), a double-base theorem proving boundary (7), a moving contact connection switch (8) and bases (9). Stable Goldbach spaces are below the double-base theorem proving boundary (7) and the maximum-equation proving boundary (6), a seamless fluctuation Goldbach space is below the one-equation proving boundary (5), and ranges, methods and natural laws for proving the Goldbach conjecture to be true are demonstrated and decided.

Description

technical field [0001] The patent of the present invention relates to the field of mathematics teaching and education technology in primary and middle schools, and the display equipment for mathematics popular science activities in public cultural places, in particular to a Goldbach conjecture proof coordinate plane demonstrator in the field of mathematics research in colleges and universities and scientific research institutes. Background technique [0002] Goldbach's conjecture is a well-known international mathematical problem, jointly edited by the Ministry of Science and Technology, the Ministry of Education, the Chinese Academy of Sciences, the National Natural Science Foundation, and Science Press, the first edition of "10000" was officially published by Science Press in 2009. The book "A Scientific Problem·Mathematics Volume" introduces Goldbach's conjecture: "An even number greater than 4 is the sum of two odd prime numbers". At present, the international mathematic...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G09B23/02
Inventor 李中平
Owner 李中平
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com