Signal arrival direction estimation method based on sparse processing
A technology of direction estimation and sparse signal vector, applied in the estimation of the angle of arrival of array signals, which can solve the problems of increasing hardware implementation difficulty, unsuitable for engineering use, and increasing the amount of received data.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
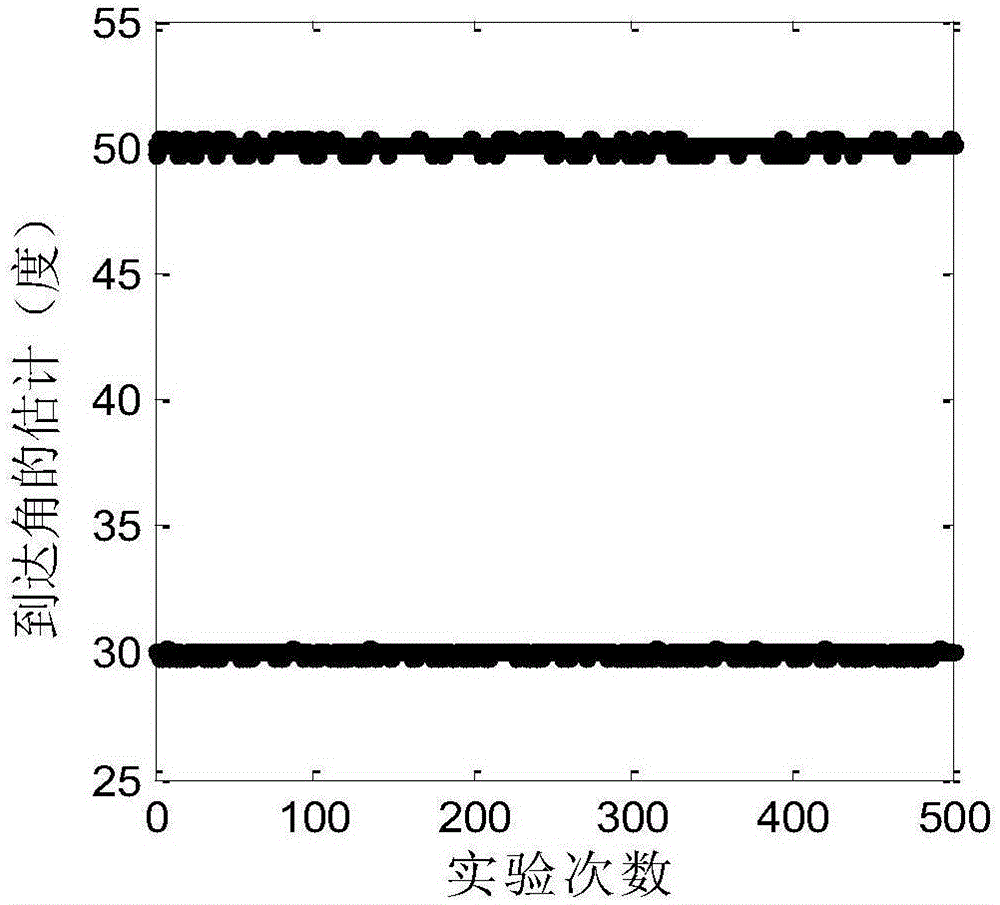
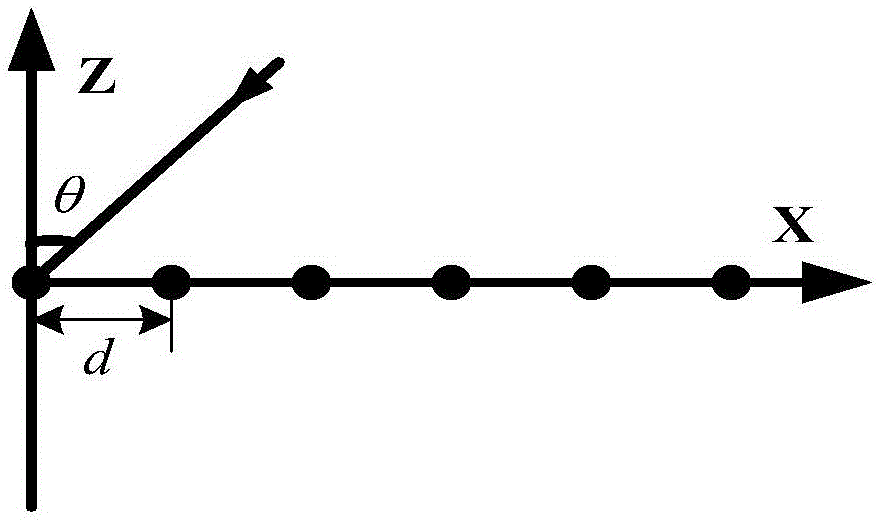
[0036] Compressed sensing theory shows that, for compressible signals or sparse signals, it is possible to break through the limitation of Nyquist sampling theorem, perform sampling operation on the original data at a lower frequency, and can accurately reconstruct the data from the sampled data according to the appropriate reconstruction algorithm. restore the original signal. The finite source of space is sparse compared to the full space, so the signal received by the receiving array is considered to be a sparse signal, and the compressed sensing theory can be used to estimate the signal angle of arrival, but the signal captured by a snapshot The anti-noise performance of the angle-of-arrival estimation algorithm is very poor. For this reason, the present invention proposes a method for estimating the signal angle-of-arrival based on compressed sensing theory, and uses low snapshot anti-noise, thereby improving the anti-noise performance of the algorithm and improving the es...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com