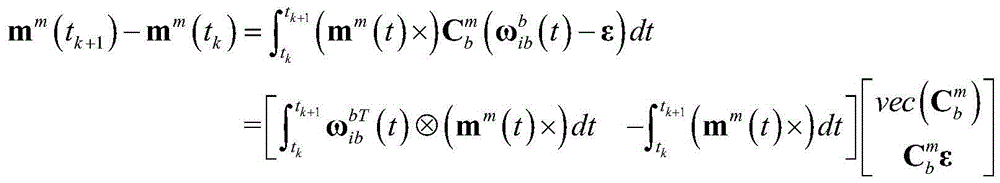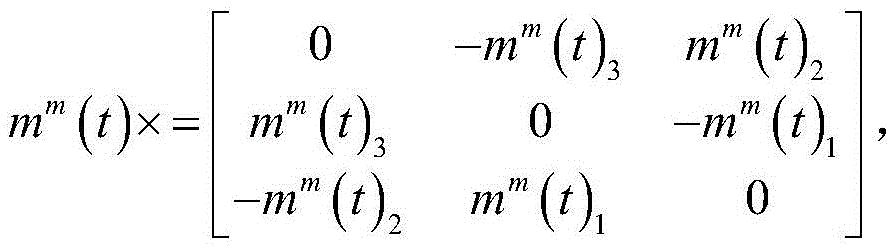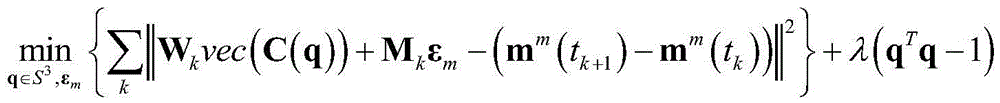Integrated calibration method for gyro and magnetic transducer
A magnetic sensor and joint calibration technology, applied in the field of sensors, can solve the problems of affecting the calibration effect of magnetometer and gyroscope, large bias error of low-cost gyroscope, inability to calibrate magnetometer, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0045] The present invention will be described in detail below in conjunction with specific embodiments. The following examples will help those skilled in the art to further understand the present invention, but do not limit the present invention in any form. It should be noted that those skilled in the art can make several changes and improvements without departing from the concept of the present invention. These all belong to the protection scope of the present invention.
[0046]In a steady magnetic field, changes in the measured values of the three-axis magnetic sensor are entirely due to changes in attitude. Based on this fact, the present invention provides a joint calibration method for the misalignment angle of the coordinate system between the three-axis magnetometer and the three-axis gyroscope and the zero bias of the gyroscope. The magnetometer is fixedly connected with the gyroscope, fully changes the attitude and collects the measurements of the magnetometer ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com