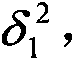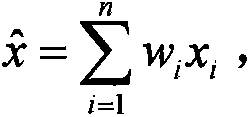D-S evidence theory-based textile process data fusion system
A technology of evidence theory and process data, applied in the field of textile data monitoring, can solve the problems of information integration models and methods that are difficult to deal with, the accuracy of data fusion results is difficult to guarantee, and the amount of data is doubled.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0040] In order to make the objects and advantages of the present invention clearer, the present invention will be further described in detail below in conjunction with the examples. It should be understood that the specific embodiments described here are only used to explain the present invention, not to limit the present invention.
[0041] Such as figure 1As shown, the embodiment of the present invention provides a textile process data fusion system based on D-S evidence theory, including a sensor module for collecting data from each workshop, a local decision-making module and a D-S synthesis module, and the sensor module and the local decision-making module correspond one-to-one The local decision-making module is connected to the D-S synthesis module. The local decision-making module adopts an adaptive weighted data fusion algorithm, which can not only optimize the data of each workshop equipment sensor, but also effectively eliminate environmental interference signals. ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com