Multi-scale iteration method for efficiently solving state of large-scale nonlinear random structure system

A nonlinear random, system state technology, applied in complex mathematical operations and other directions, can solve problems such as the inability to accurately describe environmental load characteristics, the difficulty of nonlinear dynamic response analysis methods, and the increase in the number of system states.

Active Publication Date: 2016-10-12
BEIHANG UNIV
View PDF3 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Although the application of the FPK method is promoted by means of the random averaging method and filtering method, there are still two disadvantages in this method: on the one hand, the external random excitation must be a delta-related random process or can be expressed as a white noise filter; on the other hand, the method Increased the number of states in the system
However, the vast majority of theoretical studies have neglected the improvement of the numerical solution efficiency of the moment function equation
Obviously, inefficient numerical solution algorithms will lead to difficulties in the practical application of nonlinear...

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Multi-scale iteration method for efficiently solving state of large-scale nonlinear random structure system
  • Multi-scale iteration method for efficiently solving state of large-scale nonlinear random structure system
  • Multi-scale iteration method for efficiently solving state of large-scale nonlinear random structure system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

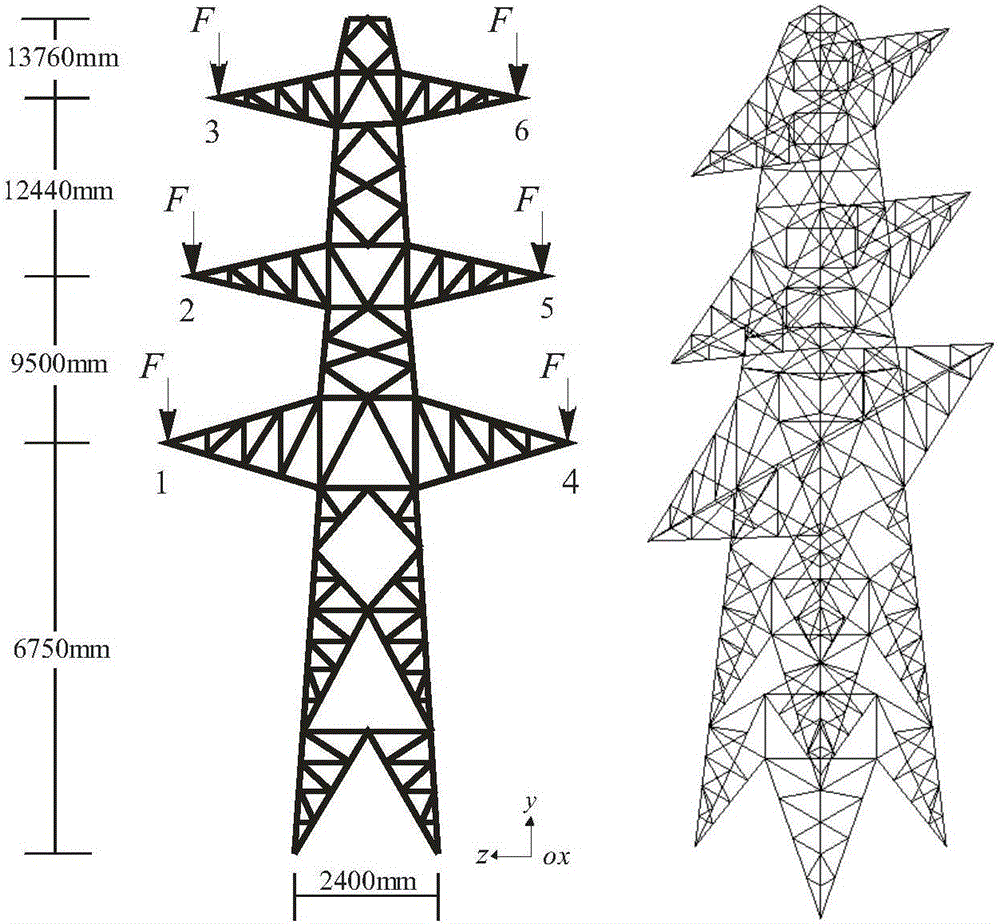
[0124] 1. Structural parameters and model introduction

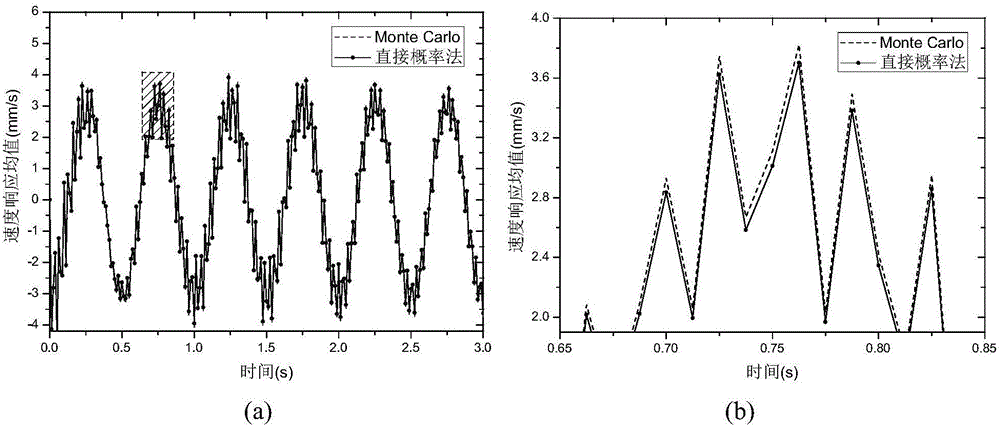
[0125] In order to understand more fully the characteristics of this invention and its applicability to engineering practice, the present invention uses figure 2 The transmission tower structure shown is taken as an example to illustrate the effectiveness of the multi-scale iterative method in efficiently solving the state response of large-scale nonlinear stochastic structural systems. Figure 4 The tower structure is mainly composed of pipes with two types of sections. The main columns are on the four sides. The modulus of elasticity of the material is 2.06×10 5 MPa, Poisson's ratio is 0.3. The tower is fixed at four bases at the bottom, and the 6 cantilever ends bear the downward concentrated load F(t)=-psin(4πt), where p is a random parameter, and its mean and standard deviation are respectively μ p = 1960N and σ p =100. Assuming that the stiffness of the structure is nonlinear, the nonlinear governing differen...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a multi-scale iteration method for efficiently solving a state of a large-scale nonlinear random structure system. The method comprises the following steps: establishing a moment function equation of a state response of the nonlinear random structure system; establishing an enclosed moment function equation of the state response by a Gauss truncation technology; establishing a multi-scale discrete interval within a time domain; and iteratively solving the enclosed moment function equation of the state response within the multi-scale interval by a Runge-Kutta method to obtain a statistical characteristic of the state response of the nonlinear random structure system finally. Through adoption of the multi-scale iteration method, simultaneous solving of three random differential equations can be avoided; a large quantity of computer storage resources are saved; and the computation efficiency is increased greatly. Moreover, iteration times can be adjusted automatically through error control and initial value setting, so that accelerated convergence of a solving process is realized. An efficient solving method is provided for state analysis of the large-scale nonlinear random structure system, and the method has an actual engineering application value.

Description

technical field [0001] The invention is mainly applicable to the efficient calculation of the statistical characteristics of the state response of a large-scale nonlinear random structure system, and specifically relates to a multi-scale iterative method for efficiently solving the state of a large-scale nonlinear random structure system. Background technique [0002] Earthquakes, wind loads and sea waves are common environmental loads. Under long-term environmental loads, the dynamic response of man-made structures will affect the function and safety of the structure. Therefore, the dynamic response analysis of structures under environmental loads is particularly important. Since environmental loads are usually treated as stochastic processes, it is necessary to establish and solve stochastic differential equations during dynamic response analysis. [0003] The Fokker-Planck-Kolmogorov (FPK) method is widely used to establish differential equations for nonlinear stochasti...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F17/15
CPCG06F17/15
Inventor 邱志平吕峥王晓军朱静静陈潇蒋文婷
Owner BEIHANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap