DOA estimation method in co-prime array based on iteration sparse reconstruction

A sparse reconstruction and DOA technology, applied in the field of DOA estimation based on iterative sparse reconstruction, can solve the problems of undetectable transmission power, difficulty in estimating performance, and affecting the effect of reconstruction, etc., to achieve low transmission power and improve estimation Accuracy and resolution, the effect of increasing the degree of freedom

Active Publication Date: 2016-10-12

SHANDONG AGRICULTURAL UNIVERSITY

4 Cites 19 Cited by

AI-Extracted Technical Summary

Problems solved by technology

[0003] The traditional estimation method usually researches the uniform linear array whose element interval is half wavelength, and is suitable for occasions where the number of detection targets is less than the number of array elements. For example, for N-antenna uniform linear arrays, traditional estimation methods (such as based on estimation method, etc.) can detect at most N-1 targets, and the nonlinear coprime array constructs the original array into a differential array with more virtual antennas and a larger aperture length by using the characteristics of the covariance matrix, which can significantly improve Its degree of freedom, that is, the detection ability, the traditional estimation method usually requires prior information on the number of targets and a large sample to estimate the direction of arrival of the target, which is not applicable under the conditions of small samples and unknown number of targets. In addition, the traditional estimation method It is also difficult to apply to the situation of low signal-to-noise ratio, that is, weak targets with low transmission power (such as less than noise power) may not be detected

[...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine

Abstract

The invention discloses a DOA estimation method in a co-prime array based on iteration sparse reconstruction. A receiving antenna array uses a nonlinear co-prime array, through vectorized processing on a second-order statistical characteristic covariance matrix of a received signal, and a difference array in larger aperture length can be determined, so as to improve detection capability. Dispersing processing is performed on the angle domain where targets are in, targets can be regarded as sparsely distributed on grid points or near grid points, and sparse signal reconstruction problems on logarithm and forms are established. Using convex compact upper bounds of logarithm and a function, an original sparse problem is reestablished, to dynamically adjust and update discrete points of the angle domain in an iterative manner, so approach the actual arrival angle of the target.

Application Domain

Computer aided designSpecial data processing applications

Technology Topic

Large apertureEstimation methods +5

Image

Examples

Experimental program(1)

Example Embodiment

[0026] The present invention will be further described in detail below in conjunction with the accompanying drawings:

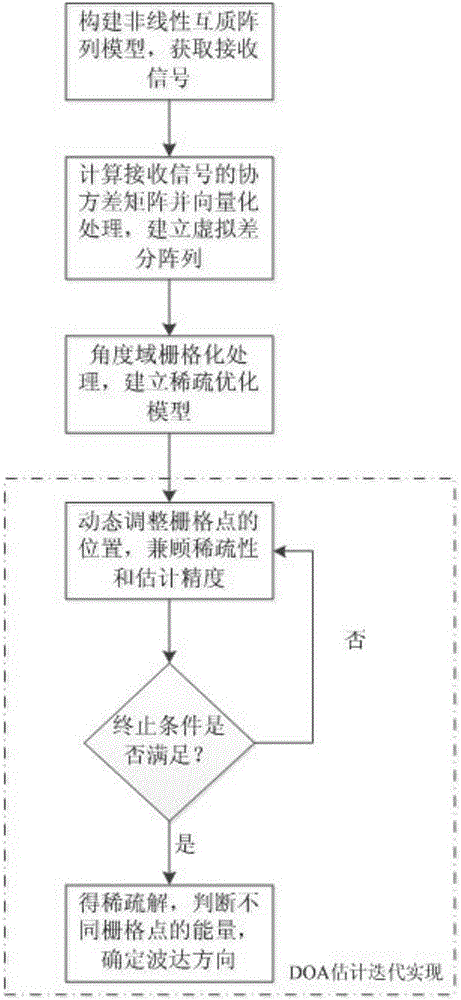
[0027] The flow chart of the method of the present invention is as figure 1 As shown, the specific implementation process is as follows:

[0028] (1) Construct a nonlinear coprime array model to obtain the received signal;

[0029] (2) Calculate the covariance matrix of the received signal and perform vectorization processing to establish a virtual difference array;

[0030] (3) Rasterize the angle domain to establish a sparse optimization problem;

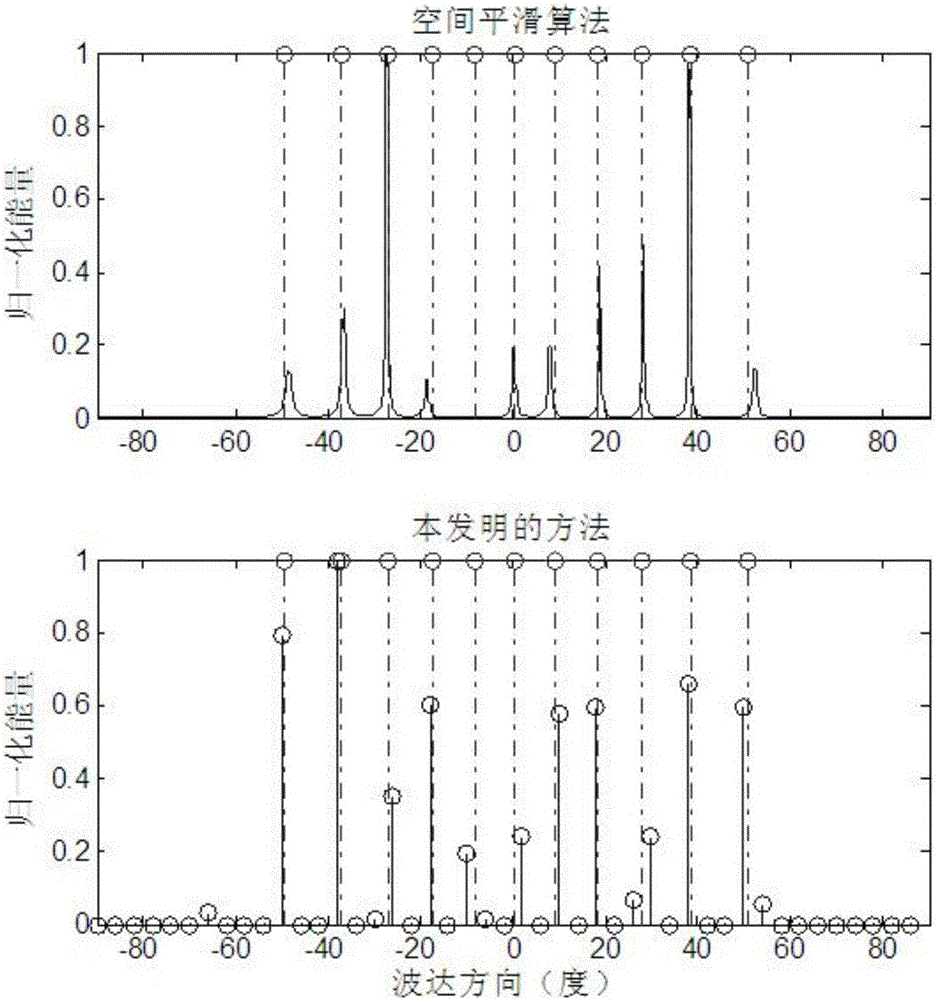
[0031] (4) Dynamically adjust the grid point position in an iterative manner until the termination condition is met. Analyze the sparse solution and determine the final direction of arrival.

[0032] The process of the DOA estimation method of the present invention is as follows:

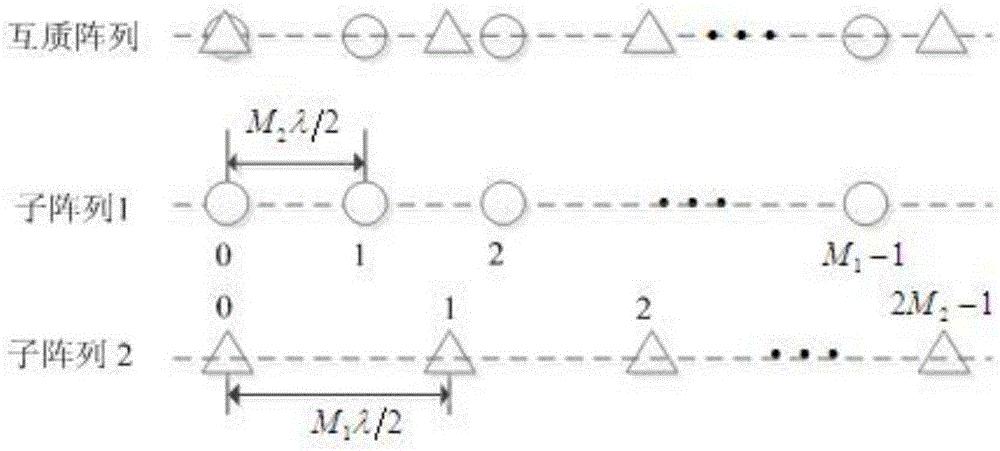
[0033] 1. Coprime array and its receiving signal

[0034] The relative prime array involved in the present invention is such as figure 2 As shown, the array can be decomposed into two uniform linear sub-arrays, where sub-array 1 contains M 1 Antennas, the distance between adjacent antennas is M 2 λ/2, sub-array 2 contains 2M 2 Antennas, the distance between adjacent antennas is M 1 λ/2, where M 1 And M 2 It is a positive integer of relatively prime, λ represents the wavelength of the carrier, the whole of sub-arrays 1 and 2 form a non-linear relatively prime array. Since sub-arrays 1 and 2 share the first antenna, the number of antennas of the relatively prime array is M=M 1 +2M 2 -1.

[0035] There are unknown number of unrelated targets (assumed to be K) from different directions Θ=[θ 1 ,θ 2 ,...,Θ K ] Arrives at the coprime array, the received signal of the array at time t (1≤t≤T) is

[0036] x ( t ) = X k = 1 K a ( θ k ) s k ( t ) + n ( t ) = A s ( t ) + n ( t ) - - - ( 1 )

[0037] Among them, A=[a(θ 1 ),a(θ 2 ),…,A(θ K )] represents the known array manifold matrix determined by the array position, s(t)=[s 1 (t),s 2 (t),...,s K (t)] T Represents the transmitted signal vectors of K targets, n(t) is the independent and identically distributed additive white Gaussian noise vector, and the superscript T represents transpose.

[0038] 2. Covariance matrix and virtual difference array

[0039] The covariance matrix of the received signal x(t) can be characterized as

[0040] R x x = E [ x ( t ) x H ( t ) ] = X k = 1 K σ k 2 a ( θ k ) a H ( θ k ) + σ 2 I M 1 + 2 M 2 - 1 - - - ( 2 )

[0041] among them, And σ 2 Respectively represent the power and noise power of the k-th signal, E represents expectation, superscript H represents conjugate transpose, Means M 1 +2M 2 -1 dimensional unit matrix, matrix R xx The (m, n) item is Can be regarded as l m -l n The received signal of the virtual antenna that exists at R xx , The virtual antenna generated by the difference between the mth and nth antennas is at position l m -l n (1≤m,n≤M 1 +2M 2 -1), l m And l n Denote the actual positions of the m and n antennas respectively.

[0042] To R xx For vectorization, there are

[0043] z=vec(R xx )=Φ(θ 1 ,θ 2 ,...,Θ K )p+σ 2 1 n , (3)

[0044] among them with vec stands for vectorization processing, Represents the Kronecker product, z is the received signal of the virtual differential array, Φ(θ 1 ,θ 2 ,...,Θ K ) Represents the array popularity matrix of the virtual differential array.

[0045] 3. Rasterization processing to establish sparse optimization problem

[0046] In order to use the sparse method for DOA estimation, the target angle domain needs to be rasterized, Therefore, the sparse optimization problem can be established as

[0047] m i n θ g , p , σ 2 | | p | | 0 , s . t . z = Φ ( θ g ) p + σ 2 1 n - - - ( 4 )

[0048] Where ||·|| 0 Represents the 0-norm. The meaning of this optimization problem is that at a given static grid point, that is, under the premise of a given virtual array popularity matrix, use as little signal power p to reconstruct the received signal z. This problem It is an NP-hard problem with a huge amount of calculation,

[0049] For this reason, the logarithm sum function is used to approximate the 0-norm in (4), and the unconstrained optimization problem is constructed as

[0050] m i n θ g , p , σ 2 η X i = 1 D l o g ( p i 2 + ϵ ) + 1 2 | | z - Φ ( θ g ) p - σ 2 1 n | | 2 2 - - - ( 5 )

[0051] Where ε> 0 is used to determine the existence of logarithmic function, ||·|| 2 Represents the least squares cost function, η> 0 measures the balance between sparsity and least squares cost. Due to the non-convexity of the logarithmic function, the optimization problem (5) is easy to fall into a local optimal solution. Further, use the logarithmic sum function Convex upper bound function

[0052] Q ( p | p ^ ( t ) ) = X i = 1 N ( | p i | 2 + ϵ | p ^ i ( t ) | 2 + ϵ + l o g ( | p ^ i ( t ) | 2 + ϵ ) - 1 ) , - - - ( 6 )

[0053] Instead of the logarithm sum function in the optimization problem, where p i Is the i-th element in p, Is p i The estimation in the tth iteration, and the unknown variables {p,θ g ,σ 2 }After irrelevant terms, optimization problem (5) can be transformed into

[0054] m i n θ g , p , σ 2 ηp H D ( t ) p + 1 2 | | z - Φ ( θ g ) p - σ 2 1 n | | 2 2 , - - - ( 7 )

[0055] among them

[0056] 4. DOA estimation iterative realization

[0057] The specific implementation steps of this iterative method are as follows:

[0058] Step 1: Initialize the discrete angle set θ g,(0) , The corresponding signal power set And noise power σ 2 , (0) , And set t = 1,

[0059] Step 2: Set θ according to the current angle g,(t-1) And noise power σ 2,(t-1) , The optimization problem (7) derivation of p and zero, calculate Get

[0060] p ^ ( t ) = ( Φ H ( θ g , ( t - 1 ) ) Φ ( θ g , ( t - 1 ) ) + 2 ηD ( t - 1 ) ) - 1 Φ H ( θ g , ( t - 1 ) ) ( z - σ 2 , ( t - 1 ) 1 n ) - - - ( 8 )

[0061] Step 3: Set θ according to the current angle g , (t-1) And signal power estimation Calculate noise power σ 2 , (t) for

[0062] σ 2 , ( t ) = 1 2 N ( z H 1 n + 1 n H z - ( Φ ( t - 1 ) p ^ ( t ) ) H 1 n - 1 n H ( Φ ( t - 1 ) p ^ ( t ) ) ) - - - ( 9 )

[0063] Step 4: Estimate according to the current signal power Construct a convex upper bound function of the logarithm sum function Update

[0064] Step 5: Convert the estimated value σ 2 , (t) And D (t) Substituting the optimization problem (7), the optimization problem becomes

[0065] m i n θ g f ( θ g ) = - ( z - σ 2 1 n ) H Φ ( θ g ) ( Φ H ( θ g ) Φ ( θ g ) + 2 ηD ( t ) ) - 1 Φ H ( θ g ) ( z - σ 2 , ( t ) 1 n ) - - - ( 10 )

[0066] Since Φ(θ g ) Is about θ g The nonlinear function of, directly obtain the optimal θ g Difficult to achieve, iterative method can be used to gradually approach the optimal θ g , To find a new estimate θ g,(t) Satisfy the following formula

[0067] f(θ g,(t) )≤f(θ g,(t-1) )

[0068] θ g , (t) It can be estimated as

[0069] θ g , ( t ) = θ g - μ ∂ f ( θ g ) ∂ θ g | θ g = θ g , ( t - 1 )

[0070] Where μ is a small positive number,

[0071] Let t=t+1,

[0072] Step 6: If the termination condition is met, the algorithm ends, otherwise skip to step 2.

[0073] The following shows the superior performance of the present invention by comparing the method of the present invention with other traditional methods (such as spatial smoothing method) through simulation:

[0074] The simulation experiment of the present invention uses M 1 = 5 and M 2 =3 coprime array model, the total number of antennas is 10, there are K=11 equal power signal sources, and the angles are [-49.3, -37.2, -26.8, -17.3, -8.3, 0.45, 9.2, 18.3, 27.8, 38.3, 50.6] degrees, the angle domain is rasterized at equal intervals at 3 degree intervals, and the signal-to-noise ratio is defined as the ratio of input power to noise power.

[0075] image 3 Is the normalized power spectrum in the simulation experiment of the present invention, where figure 2 The abscissa represents the direction of arrival, the ordinate represents the normalized energy, the dashed line represents the true angle, the solid line in the figure above represents the angle estimated by the spatial smoothing algorithm, and the solid line in the figure below represents the angle estimated by the method of the present invention, such as image 3 As shown, the method of the present invention can successfully detect all targets, but the spatial smoothing method misses one of them, so the method of the present invention has stronger detection capabilities.

[0076] Figure 4 This is the estimation accuracy map in the simulation experiment of the present invention, which quantitatively analyzes the estimation accuracy of the present invention, Figure 4 The horizontal axis represents the signal-to-noise ratio, and the vertical axis represents the estimated mean square error. Figure 5 The abscissa represents the number of samples, and the ordinate represents the estimated mean square error. Figure 4 It can be seen that under different SNR conditions, the estimated mean square error of the present invention is less than the estimation error of the spatial smoothing algorithm, which is more obvious in a low SNR environment. Figure 5 It can be seen that under the condition of different sample numbers, the estimated mean square error of the present invention is also smaller than the estimation error of the spatial smoothing algorithm, which is more obvious under the condition of small samples. Obviously, the DOA estimation accuracy of the present invention is higher than that of the existing spatial smoothing algorithm. .

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine

Login to view more

PUM

Description & Claims & Application Information

We can also present the details of the Description, Claims and Application information to help users get a comprehensive understanding of the technical details of the patent, such as background art, summary of invention, brief description of drawings, description of embodiments, and other original content. On the other hand, users can also determine the specific scope of protection of the technology through the list of claims; as well as understand the changes in the life cycle of the technology with the presentation of the patent timeline. Login to view more.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine

Login to view more

Classification and recommendation of technical efficacy words

Increase freedom
Avoid dependence

DOA estimation method in co-prime array based on iteration sparse reconstruction

AI-Extracted Technical Summary

Problems solved by technology

Abstract

Image

Examples

Example Embodiment

PUM

Description & Claims & Application Information

Similar technology patents

Side structure of automotive body

Radiographic imaging apparatus, method and program

Mobile terminal and mobile terminal commanding and controlling method

Motorcycle

Electronic component, circuit board, electronic apparatus, and method for manufacturing electronic component

Classification and recommendation of technical efficacy words

Magnetic sensor having vertical hall device and method for manufacturing the same

Image color adjustment

Actuating Device with Rotary Switch

Optimization with ruin recreate

Manufacturing method of thin film transistor

System and methods for processing analyte sensor data for sensor calibration

Method for extracting rubusoside from sweet tea leaves

Voice recognition method, apparatus and device and medium

Automatic evaluation method of upper limb motion function in stroke based on deep learning

Piecewise constant independent component analysis-based method for estimating harmonic current of power distribution network