Supercharge Your Innovation With Domain-Expert AI Agents!

Method of predicting fatigue life of power transmission tower in cold areas

A technology for fatigue life prediction and transmission towers, which is applied in electrical digital data processing, special data processing applications, instruments, etc., can solve the problems that the fatigue life prediction method of transmission towers has not been involved, and the research on fatigue life prediction of transmission towers is few. Achieve the effect of extensive promotion value, design rationality guarantee, and simple and easy method

Inactive Publication Date: 2017-10-24
STATE GRID XINJIANG ELECTRIC POWER CO ECONOMIC TECH RES INST +3
View PDF3 Cites 6 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] At present, scholars at home and abroad have achieved certain results in the research on the fatigue performance of steel materials, but there are few studies on the fatigue life prediction of transmission towers, especially the fatigue life prediction methods of transmission towers in cold regions have not yet been involved

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method of predicting fatigue life of power transmission tower in cold areas
  • Method of predicting fatigue life of power transmission tower in cold areas
  • Method of predicting fatigue life of power transmission tower in cold areas

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

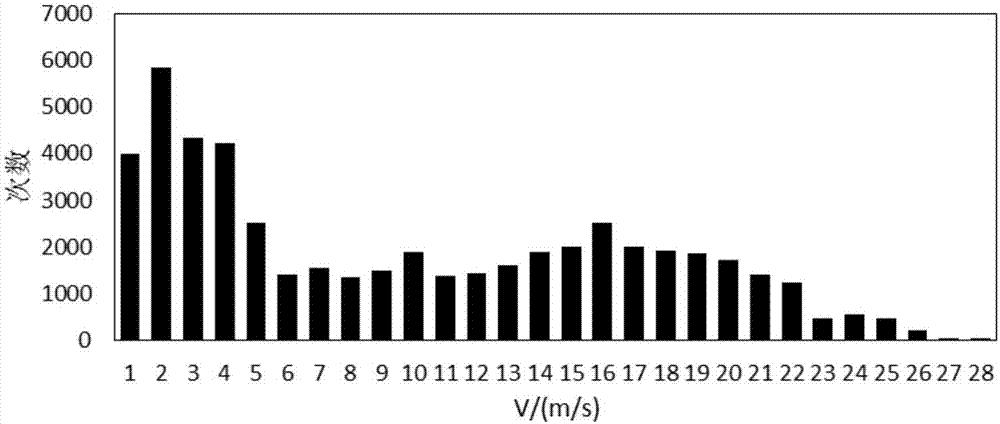
[0046] The present invention will be further described in detail below in conjunction with the accompanying drawings and embodiments. This example is a 750kV line project in a certain area in Xinjiang, with a design wind speed of 31m / s (average maximum value of 10min once in 50 years at a height of 10m), icing of 5mm, and an extreme minimum temperature of -30.0°C.

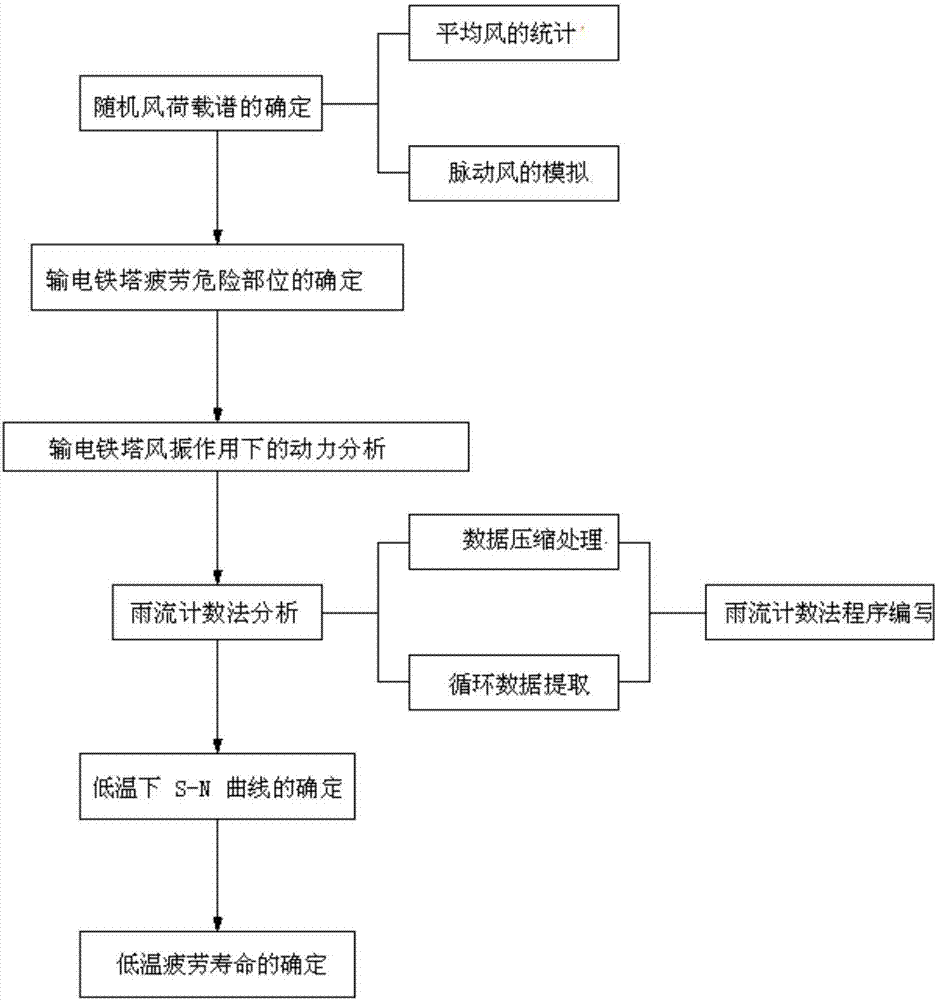
[0047] Such as figure 1 As shown, the steps of the fatigue life prediction method for transmission towers in cold regions are: determination of random wind load spectrum → determination of fatigue risk parts of transmission towers → dynamic analysis of transmission towers under wind vibration → analysis of rainflow counting method → ​​S-N curve at low temperature Determination → determination of low temperature fatigue life, the specific process is as follows:

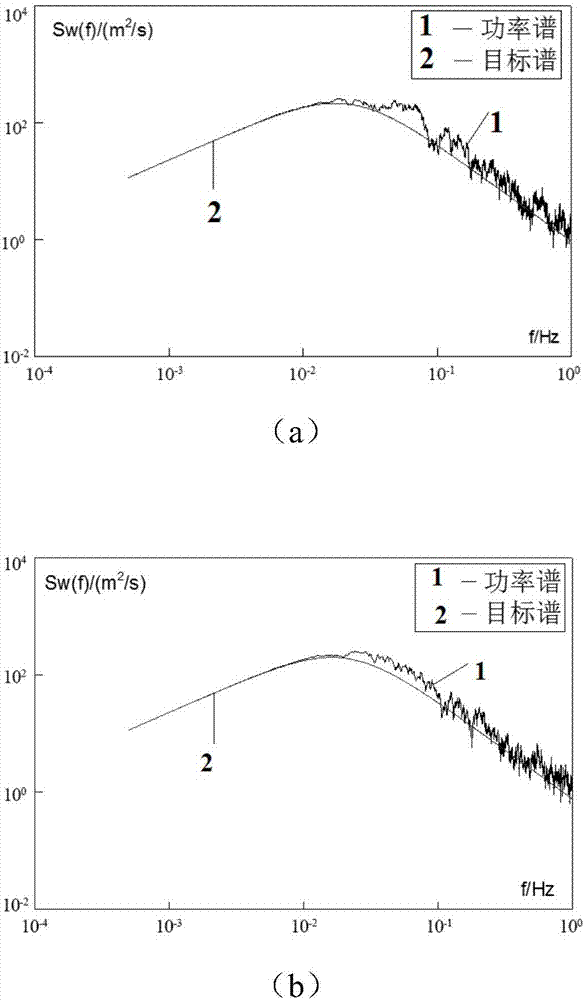
[0048] 1) Determination of the random wind load spectrum: Statistically and simulated the average wind and fluctuating wind in the cold area respectively,...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method of predicting fatigue life of a power transmission tower in cold areas and belongs to the technical field of power transmission towers. The method includes: determining a random wind load spectrum, determining a fatigue danger portion of the power transmission tower, performing dynamic analysis on the power transmission tower under wind vibration action, analyzing by a rain-flow counting method, determining an S-N curve at low temperature, and determining low-temperature fatigue life. The method has important theoretical and actual application values; by using the method to predict fatigue life of a power transmission tower in cold areas, it is possible to ensure safety, economy and reasonableness for a power transmission line of the power transmission tower in cold areas.

Description

technical field [0001] The invention relates to the technical field of power transmission towers, in particular to a method for predicting the fatigue life of power transmission towers in cold regions. Background technique [0002] With the rapid development of the national economy, the demand for power supply continues to grow, large-capacity, high-voltage transmission lines have developed rapidly, coupled with the development and utilization of wind energy in recent years, a large number of wind power stations have been established one after another. Many regions are currently vigorously developing the construction of transmission towers, especially in some extreme weather regions, such as alpine regions and perennially windy regions. Due to the special environment, higher requirements are put forward for the safety of transmission towers. [0003] In recent years, although there have been few transmission tower fatigue failures caused by wind loads, with the demand for co...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
CPCG06F30/23
Inventor 程峰周楠胡常胜吴海洋覃伟平徐彬徐玉波王金锁李俊岳华刚包永忠郭念褚忠凯李亚单强谢文李洋康建国徐世玉刘辉殷飞胡亚芳冯衡曾二贤白强夏谦王松涛王亚东赵冲
Owner STATE GRID XINJIANG ELECTRIC POWER CO ECONOMIC TECH RES INST
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com