Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

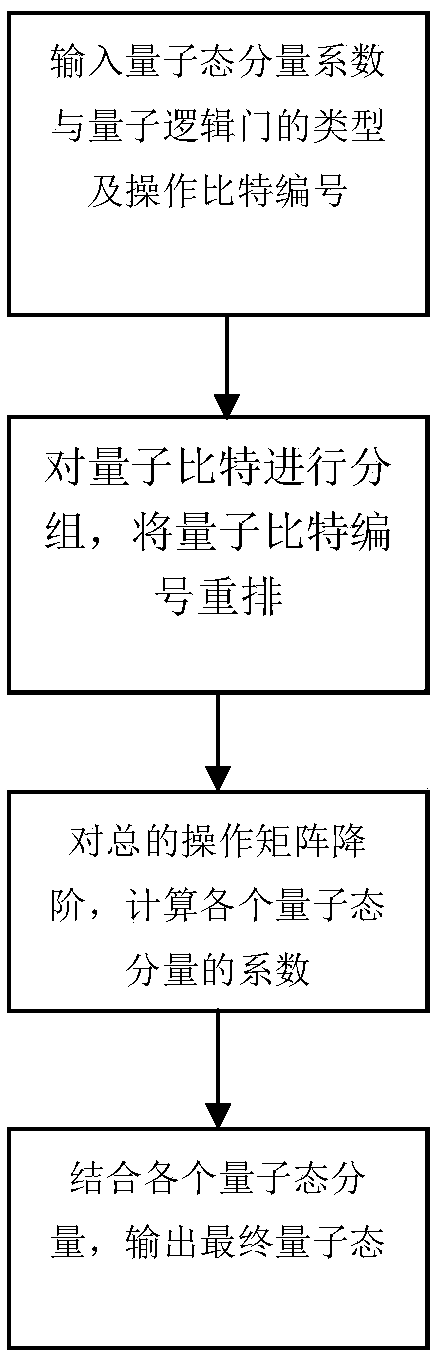
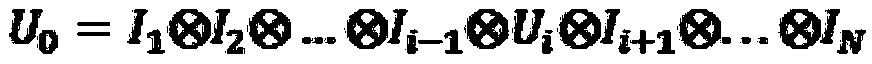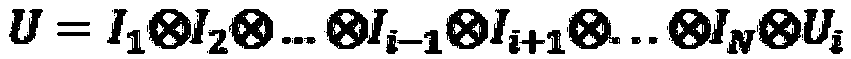Low-complexity quantum circuit simulation system

A circuit simulation, low-complexity technology, applied in the field of quantum computing, can solve problems such as inability to calculate computing time, unsuitable for simulating quantum circuits, large storage space, etc., and achieve the effect of omitting redundant operations

Active Publication Date: 2018-06-12
ORIGIN QUANTUM COMPUTING TECH (HEFEI) CO LTD
View PDF10 Cites 45 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] Aiming at the problem in the prior art that the calculation cannot be performed due to the large storage space required for matrix operations, or that the storage space is sufficient but the calculation time is too long, it is not suitable for simulating quantum circuits. The present invention provides a low-complexity simulation system for quantum circuits simulation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Low-complexity quantum circuit simulation system
  • Low-complexity quantum circuit simulation system
  • Low-complexity quantum circuit simulation system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0057] Example 1: For q 2 Do the Hadamard door operation.

[0058] Step 1: Establish a mathematical model, use To characterize the operation on the quantum system, at this time the total operation matrix U 0 with the input quantum state |θ> in0 Can be expressed as:

[0059]

[0060]

[0061]

[0062] Step 2: Group the qubits and rearrange the numbers of the qubits:

[0063] According to whether the qubit is a control bit or a controlled bit as a judgment condition, the qubits are grouped, q 1 ,q 3 ,q 4 is the cyclic bit, q 2 for operating bits.

[0064] According to the grouping results, the qubit numbers are rearranged, and the vectors for storing quantum states and the total operation matrix are rearranged according to the numbers. The rearranged quantum state |θ> in1 and the rearranged total operation matrix U 1 as follows:

[0065]

[0066]

[0067] Step 3: Reduce the order of the total operation matrix and calculate the output state

[0068] T...

Embodiment 2

[0095] Example 2: For q1q3, q1 controls the CNOT gate of q3, denoted as CNOT 1，3

[0096] Step 1: Establish a mathematical model, use Characterizing qubit logic gates.

[0097]Step 2: Group the qubits and rearrange the numbers of the qubits: according to whether the qubits are control bits or controlled bits as the judgment condition, group the qubits, q 2 ,q 4 is the cyclic bit, q 1 ,q 3 for operating bits. According to the grouping results, the qubit numbers are rearranged, and the vectors for storing quantum states and the total operation matrix are rearranged according to the numbers. The rearranged quantum state |θ> in1 and the rearranged total operation matrix U 1 as follows:

[0098]

[0099]

[0100] in,

[0101] Step 3: Reduce the order of the total operation matrix and calculate the output state

[0102] Through the new numbering and the form of the operation matrix, the 16*16 matrix can be converted into four 4*4 matrices.

[0103] Next, use the...

Embodiment 3

[0122] Example 3: Do q1q3 control q4 Toffoli gate for q1q3q4, denoted as Toffoli 1，3，4

[0123] Step 1: Establish a mathematical model, use Characterizing qubit logic gates.

[0124] Step 2: Group the qubits and rearrange the numbers of the qubits: according to whether the qubits are control bits or controlled bits as the judgment condition, group the qubits, q 2 is the cyclic bit, q 1 ,q 3 ,q 4 for operating bits. According to the grouping results, the qubit numbers are rearranged, and the vectors for storing quantum states and the total operation matrix are rearranged according to the numbers. The rearranged quantum state |θ> in1 and the total operation matrix U after rearrangement 1 as follows:

[0125]

[0126]

[0127] in,

[0128] Step 3: Reduce the order of the total operation matrix and calculate the output state

[0129] Through the new numbering and the form of the operation matrix, the 16*16 matrix can be converted into two 8*8 matrices.

[0130...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a low-complexity quantum circuit simulation system, and belongs to the field of quantum computing. The low-complexity quantum circuit simulation system overcomes the technicalproblems in the prior art that the quantum circuit simulation storage space is too large and the calculation time is too long. The system comprises an input module, a storage module and an output module, the storage process of the storage module for data is as follows: (1) a mathematical model is established to represent the operation of a quantum state and quantum logic gate; (2) quantum bits aregrouped and the serial numbers of the quantum bits are rearranged; (3) degree reduction is conducted on a total operation matrix U0, and an output state is calculated. According to the system, a matrix element of a quantum state vector is directly operated by using an connotative inherent law of a quantum logic gate, at the same time, the method has expandability, in the future, a supercomputer can be used to simulate a quantum computer with more bits.

Description

technical field [0001] The invention belongs to the field of quantum computing, and in particular relates to a program language description system based on a quantum circuit model, which is a low-time and space-complex system for simulating quantum circuits by computers. Background technique [0002] The quantum algorithm described by the quantum circuit model is a method of manipulating a quantum computer to process the input state and output a specific measurement value. When running quantum algorithms, quantum computers have become a key technology under research because of their ability to deal with mathematical problems more efficiently than ordinary computers, such as accelerating the time to crack RSA keys from hundreds of years to hours . The processing speed of quantum computers increases exponentially with the number of qubits. It is expected that when the number of qubits exceeds 50, the processing speed of quantum computers on specific problems will be faster th...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06N99/00
CPCG06N10/00
Inventor 朱美珍杨夏
Owner ORIGIN QUANTUM COMPUTING TECH (HEFEI) CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com