Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

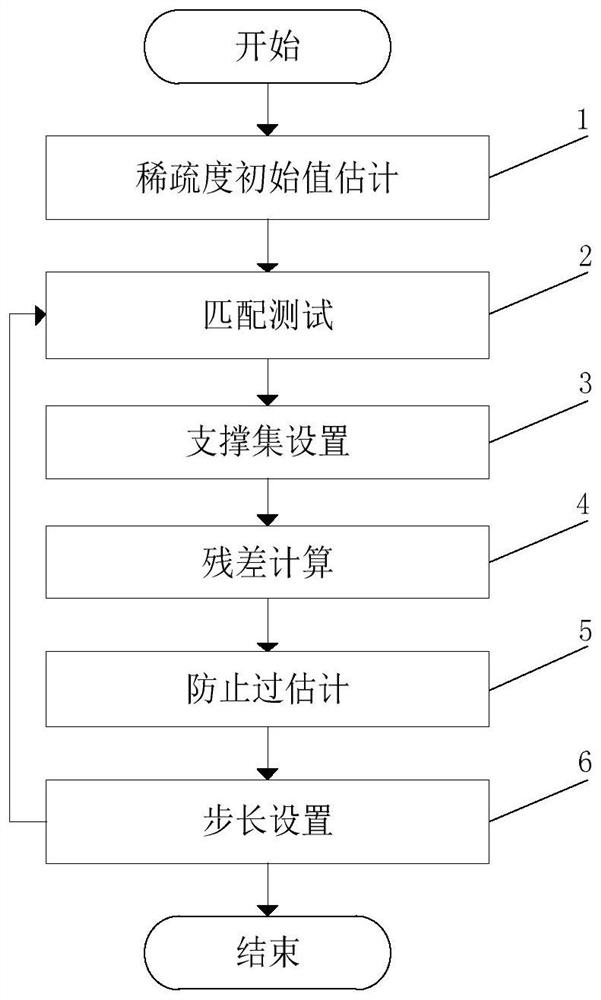
Sparsity Adaptive Variable Step Size Matching and Pursuit Method Based on Compressed Sensing

A compressed sensing and matching tracking technology, applied in code conversion, electrical components, etc., can solve the problems of long reconstruction time, overestimation or underestimation, and unimproved reconstruction time of the SAMP method, achieving reconstruction accuracy and computational complexity. High degree of consideration, avoid overestimation and underestimation, reduce the effect of computational complexity

Active Publication Date: 2022-03-04
宿州市艾尔新能源有限公司
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Among them, the SAMP method uses a fixed step size to estimate the sparsity of the signal, which can easily lead to overestimation or underestimation, and the SAMP method takes a long time to reconstruct
The SASP method can estimate the sparsity more accurately by using variable step size, but the reconstruction time does not improve
The AStMP method uses an adaptive step size to estimate the sparsity, and reduces the amount of calculation through pre-selection, but the reconstruction accuracy is easily affected by the finite isometric parameter δ P Impact

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Sparsity Adaptive Variable Step Size Matching and Pursuit Method Based on Compressed Sensing
  • Sparsity Adaptive Variable Step Size Matching and Pursuit Method Based on Compressed Sensing
  • Sparsity Adaptive Variable Step Size Matching and Pursuit Method Based on Compressed Sensing

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

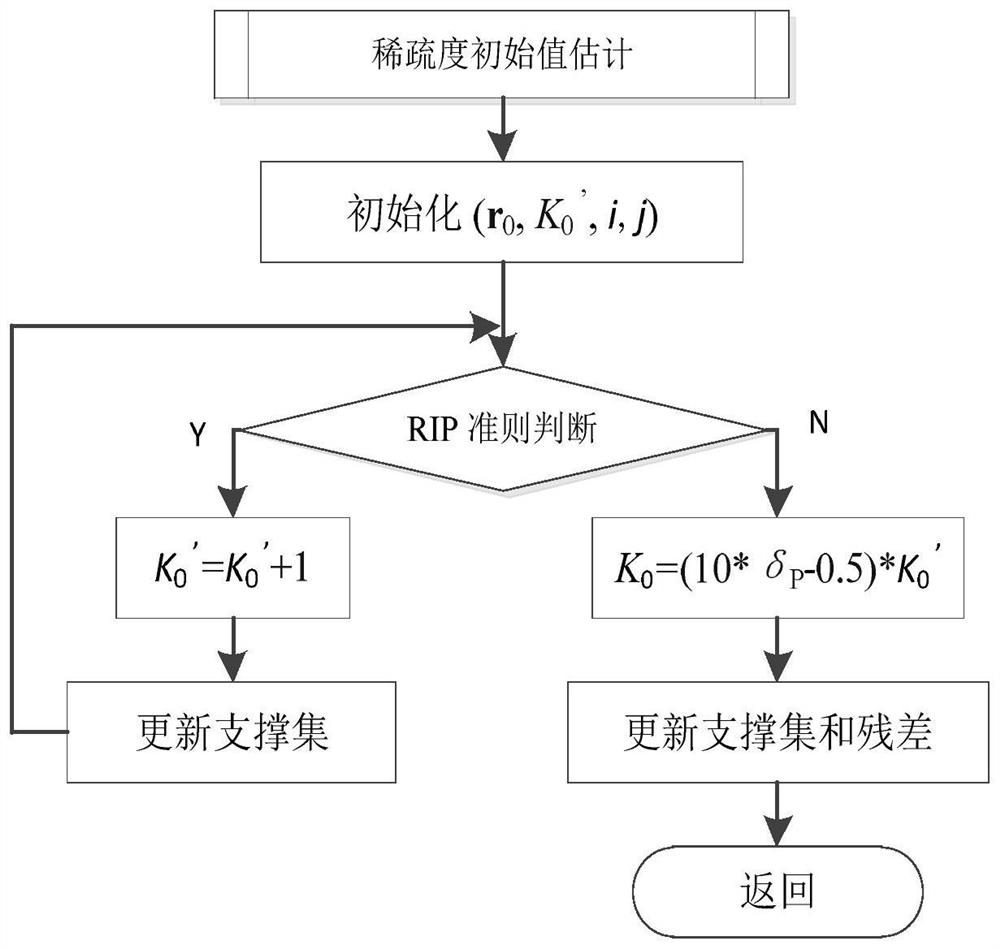
[0150] Example 1. Estimate the initial value K of the sparsity degree with the estimation module of the initial value of the degree of sparsity 0 .

[0151] A) Input measurement matrix Φ, observed signal y, RIP parameter δ P , using a Gaussian sparse signal with a mean value of 1 and a variance of 0, the length of the signal is N=256, the degree of sparsity P=44, and the number of measurements M=128.

[0152] B) Estimate the initial value of sparsity K' with SAVSMP method 0 . δ P The initial value K' of the sparsity estimated when taking 0.1, 0.15, 0.25, 0.35 respectively 0 Such as Figure 4 shown. Visible δ P When taking a smaller value, the estimated K'0 Larger, often in an overestimated state, when δ P When taking a larger value, the estimated K' 0 Small and often underestimated.

[0153] C) Use the SAVSMP method to adjust the initial value of the sparsity K' 0 Perform adaptive processing to get K 0 , using the AStMP method to process the sparsity estimate K 0 ...

Embodiment 2

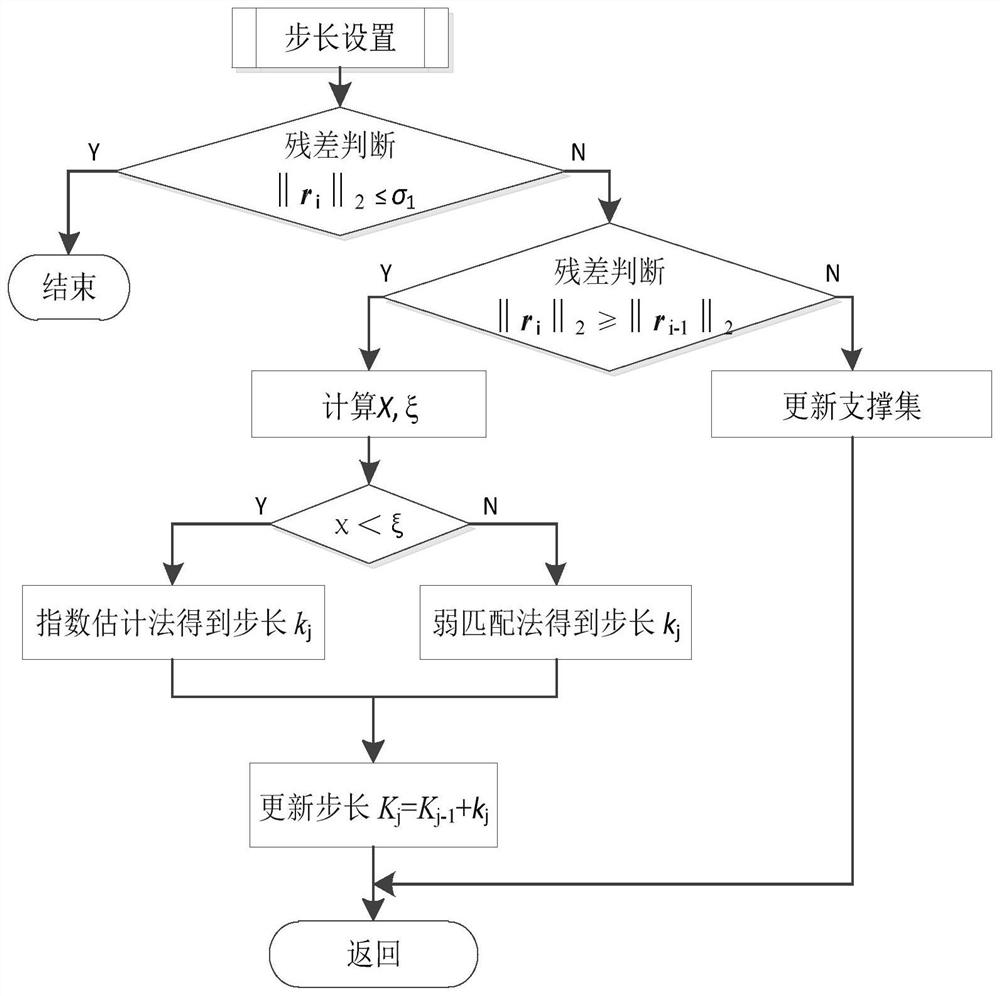
[0154] Embodiment 2. Using the step size setting module to adaptively set the step size.

[0155] A) Input measurement matrix Φ, observed signal y, RIP parameter δ P , using a Gaussian sparse signal with a mean value of 1 and a variance of 0, the length of the signal is N=256, the degree of sparsity P=44, the number of measurements M=128, and the parameter σ 1 =1×10 -6 ,σ 2 =10, weak matching parameter τ=0.9.

[0156] B) Use the SAVSMP method to set the large step size obtained by the exponential estimation method to approximate the real sparsity, and the step size change coefficient is recorded as β, and the change curve is as follows Image 6 shown.

[0157] C) Use the SAVSMP method to set the small step size obtained by the weak matching method to approximate the real sparsity.

[0158] D) Update the step size K with the SAVSMP method j .

Embodiment 3

[0159] Example 3. Comparison of SAMP method, SASP method, AStMP method, and SAVSMP method for estimating the sparsity K.

[0160] A) Input measurement matrix Φ, observed signal y, RIP parameter δ P , using a Gaussian sparse signal with a mean value of 1 and a variance of 0, the length of the signal is N=256, the degree of sparsity P=44, the number of measurements M=128, and the parameter σ 1 =1×10 -6 ,σ 2 =10, weak matching parameter τ=0.9.

[0161] B) Set the step size L=4, use the SAMP method to estimate the sparsity K, the relationship curve between the number of iterations and the estimated sparsity K is as follows Figure 7 shown. It can be seen that the SAMP method has a large number of iterations, and it takes about 22 iterations to estimate the sparsity.

[0162] C) Setting δ P = 0.1, using the SASP method to estimate the sparsity K, the relationship curve between the number of iterations and the estimated sparsity K is as follows Figure 7 shown. It can be see...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a sparseness adaptive variable step-size matching tracking method based on compressed sensing. The estimated initial value is adaptively processed in the sparseness initial value estimation part, so as to avoid over-estimation and under-estimation of the sparseness initial value; In the construction part, the Dice coefficient is used to accurately select atoms and the step size is set to a fixed constant under large number of stages, so it has high reconstruction accuracy; in the initial value estimation part of the sparsity, the initial value of the sparsity is initialized, and in the reconstruction part, the initial value of the sparsity is initialized. The step size is adapted to be set, so that the large step size obtained by the exponential estimation method is used to approximate the true sparsity, and then the small step size obtained by the weak matching method is used to approximate the true sparsity. Therefore, the present invention has lower computational complexity; The invention realizes a high degree of consideration of reconstruction accuracy and computational complexity, and meets the use requirement of accurately reconstructing the original signal in a complex electromagnetic environment.

Description

technical field [0001] The invention relates to a sparsity adaptive variable step size matching tracking method based on compressed sensing. Background technique [0002] In 2006, Emmanuel Candès, Justin Romberg and others proposed that sparse or compressed signals can be accurately reconstructed in wavelet, Fourier and other transform domains, which is the famous Compressed Sensing (CS) theory. Compressed sensing theory is a new signal sampling theory. Under the condition of far smaller than the Nyquist sampling rate, it uses the sparse characteristics of the signal to accurately reconstruct the signal through the reconstruction algorithm. CS theory processes signal sampling and compression synchronously, which not only saves hardware resources such as storage space, but also speeds up software processing speed. Therefore, this theory is widely used in pattern recognition, image processing, optical / microwave imaging, wireless communication, earth science, biomedical engine...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H03M7/30
CPCH03M7/3062
Inventor 李娜李海涛李萍郭焕银
Owner 宿州市艾尔新能源有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com