[0057] The present invention will be further illustrated below in conjunction with examples: the examples of the present invention are illustrative and do not limit the scope of protection of the present invention. Any equivalent changes made by those skilled in the industry on the basis of the technical solution of the present invention are also within the scope of patent protection of the present invention.
[0058] The specific embodiments of the present invention will be further described below in conjunction with the drawings.
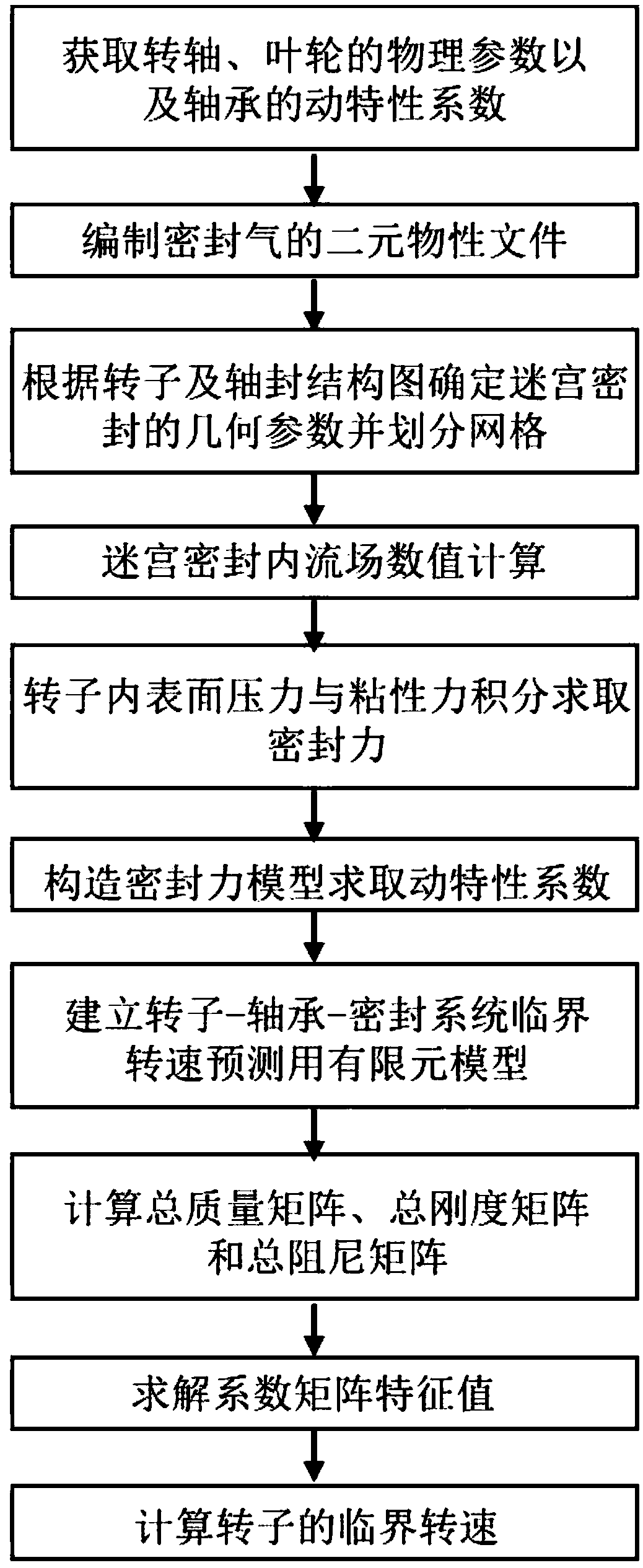
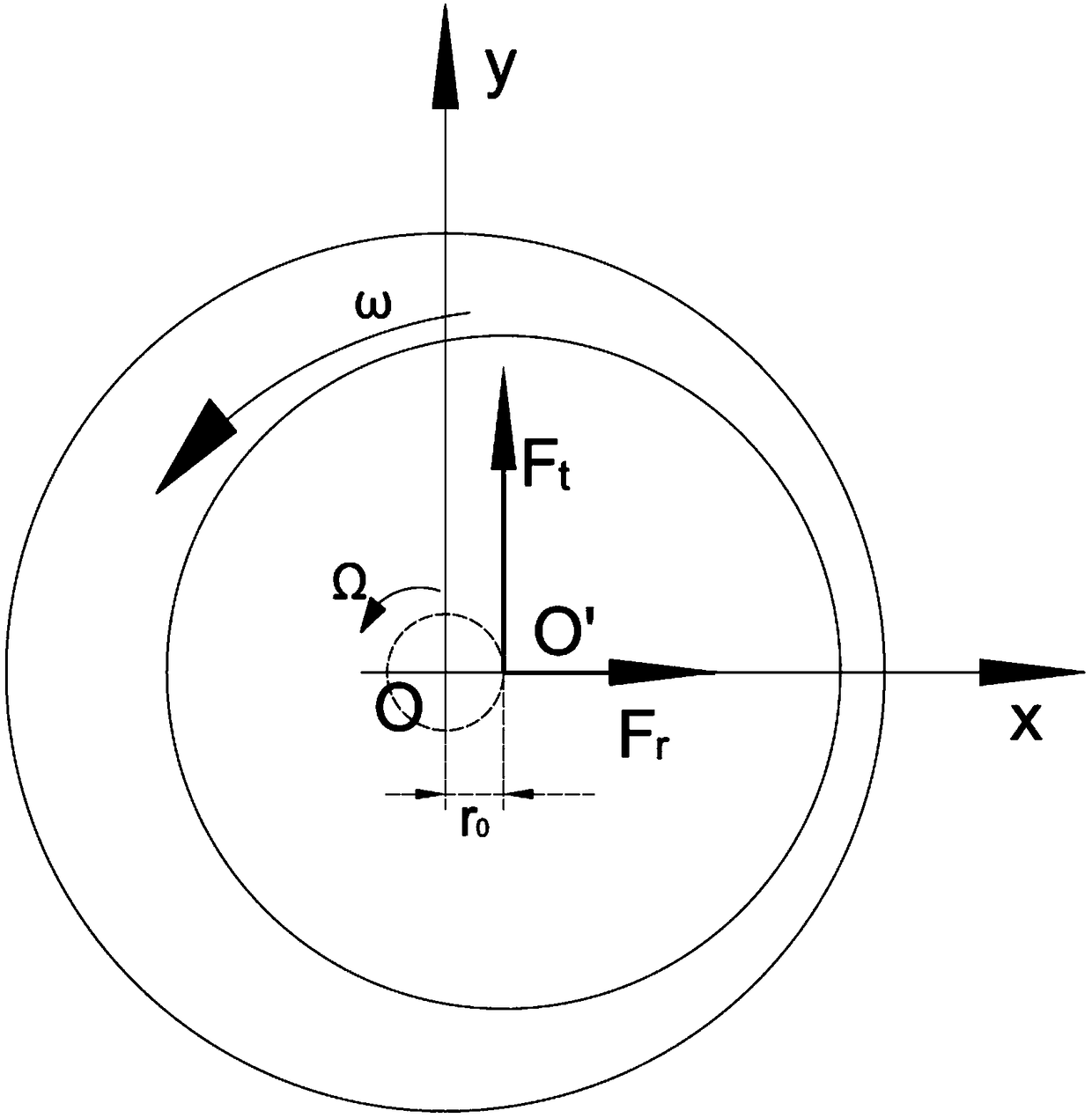
[0059] See figure 1 , A method for predicting the critical speed of the cryogenic liquid expander rotor considering the influence of the sealing force, including analyzing and obtaining the relevant physical parameters of the liquid expander rotor and bearing, using the vortex rotor method to simulate the flow field of the labyrinth seal, calculating the sealing force, and sealing dynamics Calculation of characteristic coefficients, and prediction of the critical speed of the cryogenic liquid expander rotor considering the influence of sealing force. That includes the following 5 aspects:
[0060] 1. Analyze and obtain the relevant physical parameters of the rotating shaft and impeller of the liquid expander and the dynamic characteristic coefficients of the bearing, including obtaining the geometric and material parameters of the rotating shaft and impeller, as well as the stiffness coefficient and damping coefficient of the bearing.
[0061] 2. Based on the vortex rotor model, simulate the flow field of the labyrinth seal of the cryogenic liquid expander, which mainly includes the compilation of the binary (pressure and temperature) physical property files of the seal gas; determine the geometric parameters of the labyrinth seal and divide the network according to the structure of the rotor and shaft seal Grid; Based on the vortex rotor model, numerically predict the inner flow field of the labyrinth seal of the liquid expander.
[0062] 3. Calculate the sealing force of the cryogenic liquid expander, integrate the pressure on the rotor surface and the viscous force to find the sealing force acting on the shaft.
[0063] 4. The calculation of the dynamic characteristic coefficient of the labyrinth seal mainly includes constructing the sealing force model, solving the sealing stiffness coefficient and damping coefficient, etc.
[0064] 5. The prediction of the critical speed of the cryogenic liquid expander rotor considering the influence of the sealing force mainly includes the construction of the rotor-bearing-seal system dynamic model, the calculation of the mass-stiffness-damping matrix, the calculation of the coefficient matrix, the solution of eigenvalues, and the consideration of the influence of the sealing force Rotor critical speed prediction, etc.
[0065] See figure 1 , The specific steps are as follows:
[0066] Step 1. Analyze and obtain the relevant physical parameters of the shaft and impeller of the liquid expander and the dynamic characteristic coefficients of the bearing, which mainly includes finishing the geometric parameters of the shaft and the impeller, as well as the material density, stiffness and Poisson's ratio, the position of the bearing, the stiffness coefficient and the damping coefficient.
[0067] Step 2: Based on the vortex rotor simulation, simulate the flow field in the labyrinth seal of the cryogenic liquid expander. mainly includes:
[0068] (1) Construct a binary (pressure and temperature) physical property file of the sealing gas to describe the thermodynamic properties of the fluid. The specific process is: express the specific heat capacity, thermal conductivity, dynamic viscosity and density of the sealed gas as a binary function of temperature and pressure, and compile it into a physical property file suitable for the flow field solver interface.
[0069] (2) According to the structure of the rotor and the seal, a physical model of the labyrinth seal of the cryogenic liquid expander is established and the mesh is divided to obtain the flow field in the labyrinth seal.
[0070] (3) Solve the flow field in the labyrinth seal based on the vortex rotor model. The specific process is: solving the inner flow field of the labyrinth seal in combination with the binary physical property file of the seal gas, and obtaining the inner flow characteristics of the labyrinth seal, including the pressure distribution in the labyrinth seal.
[0071] Step 3. The sealing force in the labyrinth seal of the cryogenic liquid expander is obtained through the following steps:
[0072] By integrating the pressure and viscous force area on the inner surface of the rotor, the radial component F of the sealing force acting on the rotor is obtained r And tangential component F t.
[0073]
[0074]
[0075] Where R is the rotor radius, l is the seal length, F r And F t They are the radial and tangential components of the sealing force acting on the rotor.
[0076] Step 4, the calculation of the dynamic characteristic coefficient of the labyrinth seal, mainly includes:
[0077] The gas sealing force in the labyrinth seal is formed by the airflow in the uneven circumferential gap. The effect of the sealing force on the rotor is converted into a "gas film" similar to the oil film of a tilting pad bearing, with 4 stiffness coefficients and 4 A damping coefficient calculation.
[0078] (1) According to the linearization model, the sealing force can be determined as a linear function of displacement and velocity;
[0079]
[0080] Where K xx ,K yy Main stiffness coefficient, K xy ,K yx Is the cross stiffness coefficient, C xx ,C yy Main damping coefficient, C xy ,C yx Is the cross stiffness coefficient. At the same time, when the rotor makes a circular vortex relative to the center, considering the axial symmetry, K xx =K yy =K s , K xy =-K yx =k s , C xx =C yy =C s , C xy =-C yx = C s; K s , K s , C s With c s Is unknown;
[0081] (2) Solve the stiffness coefficient and damping coefficient
[0082] Such as figure 2 As shown, at the initial moment, x(0)=r 0 ,y(0)=0, Where r 0 Is the eccentricity, Ω is the whirl speed, the tangential and radial components of the sealing force acting on the rotor:
[0083] F r =-(K s +c s Ω)r 0
[0084] F t =(k s -c s Ω)r 0
[0085] The above equations have four unknowns, calculate the corresponding F under two different Ω values r And F t , And then obtain the main stiffness coefficient K s ,Cross stiffness coefficient k s , The main damping coefficient C s , Cross damping coefficient c s.
[0086] Step 5. Prediction of the critical speed of the cryogenic liquid expander rotor considering the influence of the sealing force
[0087] (1) Establish a finite element model for the prediction of the critical speed of the rotor-bearing-seal system
[0088] Determine the rotor node number and coordinate value according to the geometric parameters of the rotating shaft and impeller in step 1, the node number and inner and outer diameter of the shaft unit, the node number, inner and outer diameter and thickness of the disc unit, the node number where the bearing and seal gas unit are located, The stiffness coefficient and damping coefficient of the bearing; to obtain the main stiffness coefficient K of the sealing gas according to step 4 s ,Cross stiffness coefficient k s , The main damping coefficient C s , Cross damping coefficient c s Establish a finite element model for the prediction of the critical speed of the rotor-bearing-seal system.
[0089] (2) Calculate the total mass matrix M, the total stiffness matrix K and the total damping matrix C, the specific process is as follows:
[0090] The calculation model equation of the rotor critical speed is
[0091]
[0092] Using the finite element method, each coefficient matrix is obtained, where M is the total mass matrix, K is the total stiffness matrix after considering the sealing gas, and C is the total damping matrix after considering the sealing gas.
[0093] (3) Solving the coefficient matrices A and B, the specific process is as follows:
[0094] Let U=Xe λt ,then The calculation model equation of the rotor critical speed is rewritten as
[0095] (λ 2 M+λC+K)X=0
[0096] Further expressed as
[0097]
[0098] Where I is the identity matrix.
[0099] make Then there is
[0100] AY=λBY
[0101] The coefficient matrices A and B can be obtained through the above modification.
[0102] (4) Solve the eigenvalue
[0103] The QZ algorithm that does not require inversion operation is used to solve the generalized eigenvalues of the coefficient matrix A relative to B, to avoid the calculation overflow when the coefficient matrix is singular, and obtain the generalized eigenvalues λ of the coefficient matrix A relative to B.
[0104] (5) Prediction of rotor critical speed considering the influence of sealing force
[0105] The imaginary part ω of the generalized eigenvalue λ of the coefficient matrix A relative to B is the natural frequency of the rotor vibration. The rotation speed n is uniformly increased (that is, n=n+Δn) and repeated iterations, and the coefficient matrix A relative to B can be obtained The series value of the imaginary part ω of the generalized eigenvalue. Fitting the imaginary part of the eigenvalue to the curve, solving the intersection of this curve and the ω=n straight line, the critical speed of the corresponding order can be obtained.
[0106] The invention considers the influence of the sealing gas flow characteristics in the labyrinth seal of the cryogenic liquid expander on the dynamic behavior of the rotor under real conditions, so that the prediction of the critical speed is more scientific, reasonable and practical. The prediction method involved in the present invention has a simple and clear flow, and has practical guiding significance for the design and stable operation of the cryogenic liquid expander rotor.
