Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Adaptive matching tracking signal reconstruction method based on group sparse structure

A technology of adaptive matching and signal reconstruction, applied in the direction of electrical components, code conversion, etc., can solve the problems of simplification and large amount of calculation.

Active Publication Date: 2019-03-29
SOUTHEAST UNIV
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] Since the introduction of the "spike and slab" prior probability distribution will transform the problem into a strictly non-convex problem, the existing reconstruction methods all have the problem of too much calculation or simplify the assumption of the prior probability distribution

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Adaptive matching tracking signal reconstruction method based on group sparse structure
  • Adaptive matching tracking signal reconstruction method based on group sparse structure
  • Adaptive matching tracking signal reconstruction method based on group sparse structure

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

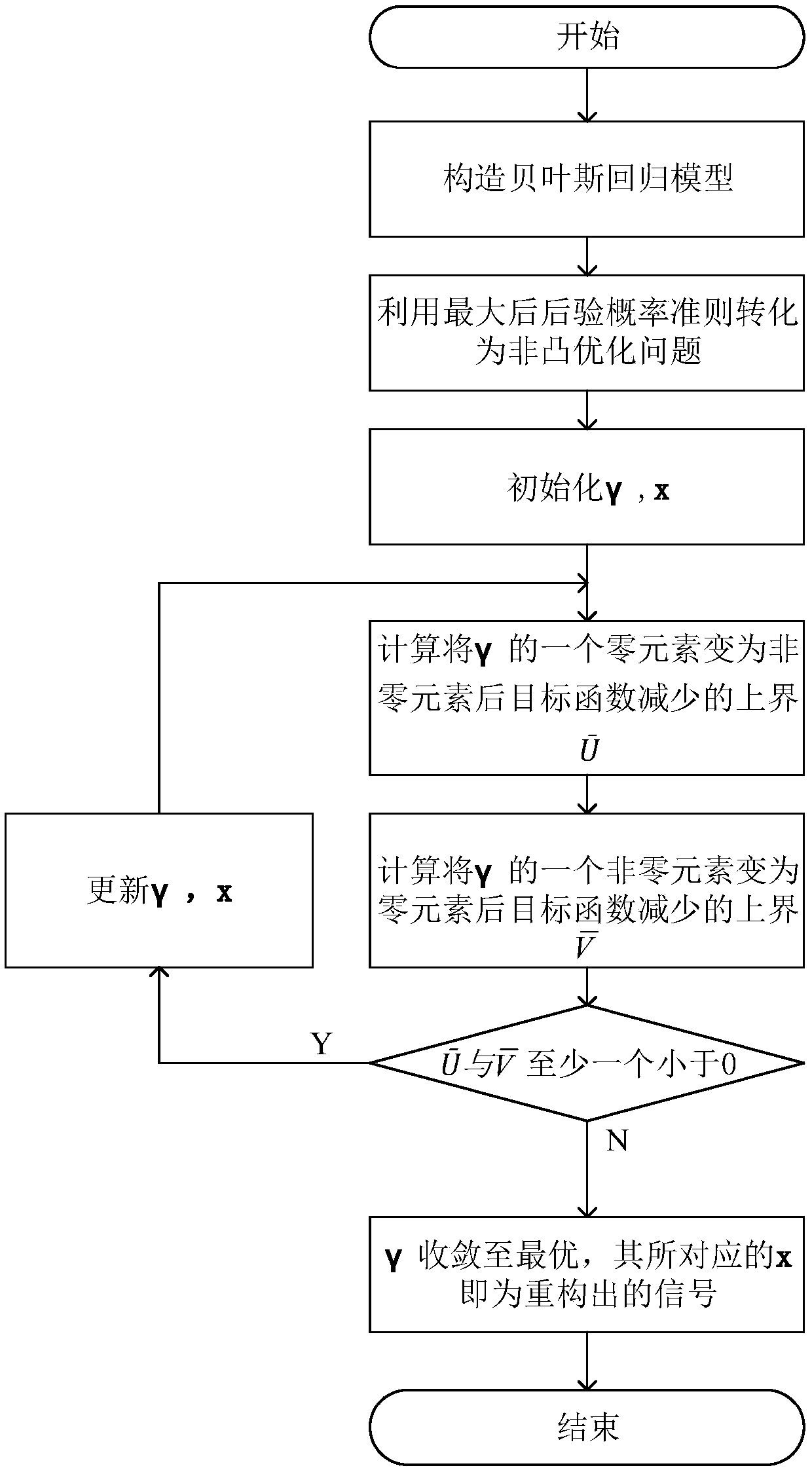
[0066] Such as figure 1 , a kind of adaptive matching pursuit signal reconstruction method based on group sparse structure, described method comprises the following steps:

[0067] Step 1. Construct a Bayesian regression model with group sparse structure:

[0068] Introduce the "spike and slab" prior probability distribution, and the regression model based on the group sparse structure is as follows:

[0069]

[0070] in,

[0071]

[0072] A is a q×p-dimensional observation matrix, and x is a p-dimensional vector. In order to express the group structure of x, the vector x is evenly divided into K groups, and the number of elements in each group is L, so p=K×L, as in the formula ( 2), where x i represents the i-th group in the x vector, and x il for x i The lth element in the vector. y represents the q-dimensional observation vector and qq Indicates the identity matrix of q×q dimension; N(·) is Gaussian distribution, I(·) is an indicator function, when the condition...

Embodiment 2

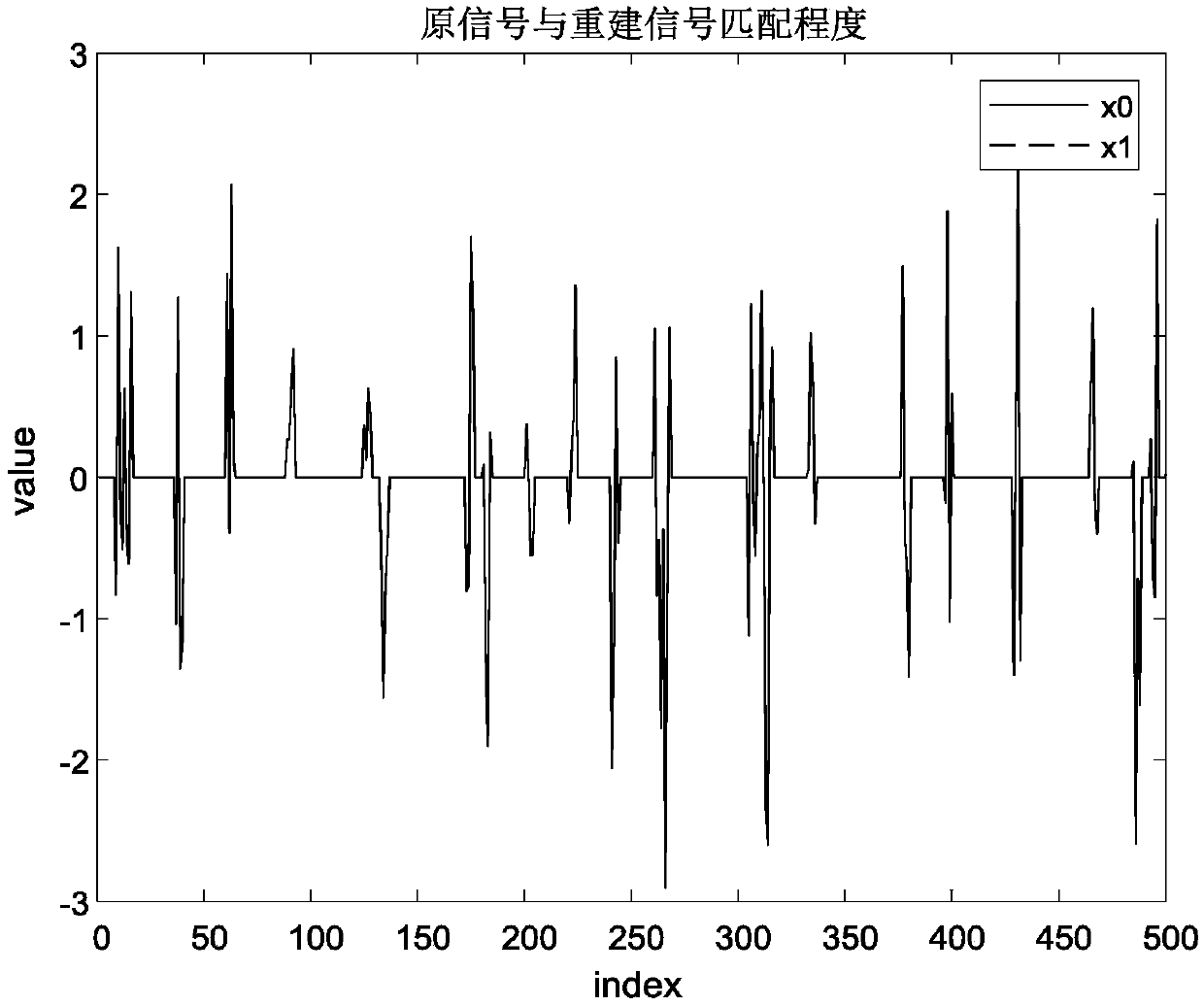
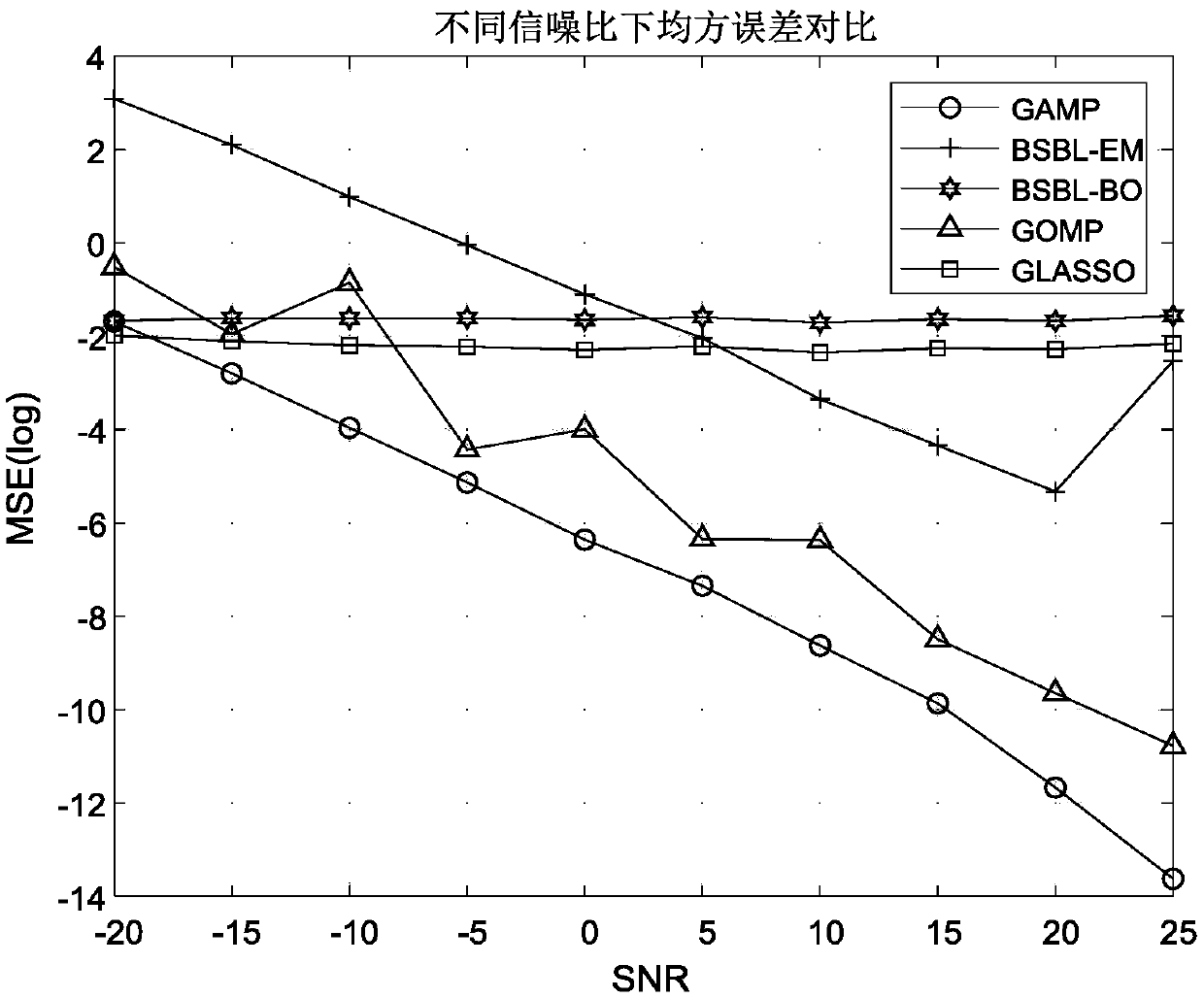
[0112] This embodiment mainly compares the mean square error of the signal reconstruction method based on the group sparse structure disclosed in the present invention and other existing group sparse signal reconstruction methods under different observation numbers, except that the signal-to-noise ratio is always 0dB and the number of observations is constant Except for changes, all the other parameter settings are the same as in Example 1. Such as Figure 4 As shown, the horizontal axis represents the number of observations, and the vertical axis represents the mean square error. The names of the signal reconstruction methods corresponding to each broken line are shown in the figure. It can be seen from the figure that when the number of observations is less than 180, the mean square error of the existing group sparse signal reconstruction method and the group sparse signal reconstruction method disclosed in the present invention are relatively large. When the number of obser...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

An adaptive matching tracking signal reconstruction method based on a group sparse structure comprises the following steps: (1) constructing a Bayesian regression model with the group sparse structureby introducing "spike and slab" prior probability distribution; (2) converting the parameter solving problem of the above model into a non-convex optimization problem about the model parameters gammaand x by utilizing a maximum posterior probability criterion; (3) initializing the gamma and x; (4) calculating an upper bound (FORMULA referred) of the reduction of the objective functions after changing a non-zero element of the gamma into a zero element; (5) calculating an upper bound (FORMULA referred) of the reduction of the objective functions after changing a zero element of the gamma intoa non-zero element; (6) when there is at least one of (FORMULA referred) and (FORMULA referred) less than zero, and if (FORMULA referred) is greater than (FORMULA referred), changing the gamma element corresponding to the (FORMULA referred) into a non-zero value, and if (FORMULA referred) is greater than (FORMULA referred), changing the gamma element corresponding to the (FORMULA referred) into zero; (7) solving the corresponding x when the current gamma is determined; (8) when at least one of (FORMULA referred) and (FORMULA referred) is less than zero, repeating the steps (4)-(7), when boththe (FORMULA referred) and (FORMULA referred) are greater than zero, stopping the repetition, and converging the gamma to the optimal value; and (9) determining that the x corresponding to the optimum gamma is the reconstructed signal.

Description

technical field [0001] The invention belongs to the field of signal processing compressed sensing, and in particular relates to an adaptive matching tracking signal reconstruction method based on a group sparse structure. Background technique [0002] Over the past decade, sparsity has been one of the hottest research topics in signal processing applications. The sparse representation of the signal allows us to represent high-dimensional data using a small number of observations. In the sparse reconstruction theory, the signal can be expressed as a linear combination of finite atoms in the observation matrix. The existence of sparsity in the signal allows us to extract relevant signals from the potential information of the data in an effective way. This kind of technology has been widely used in image restoration, signal reconstruction, dictionary learning and image denoising and other fields. [0003] The purpose of sparse reconstruction methods is to recover the original...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H03M7/30
CPCH03M7/3062Y02T10/40
Inventor 武其松刘佳豪方世良
Owner SOUTHEAST UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com