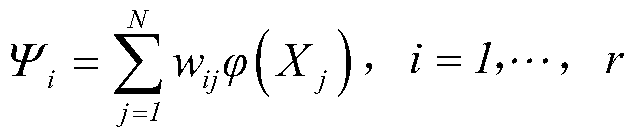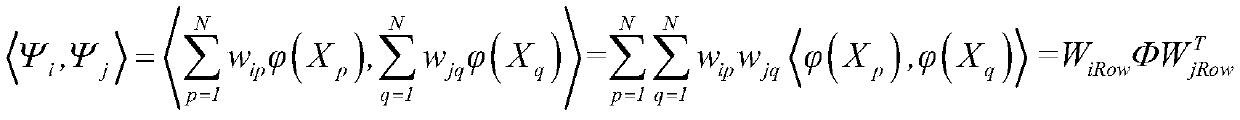Grassmann manifold domain self-adaption method based on symmetric matrix space subspace learning
A Glassmannian manifold and subspace learning technology, applied in the field of machine learning, can solve problems such as few people touch, and achieve the effect of simple model construction, low computational complexity, and intuitive physical meaning
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
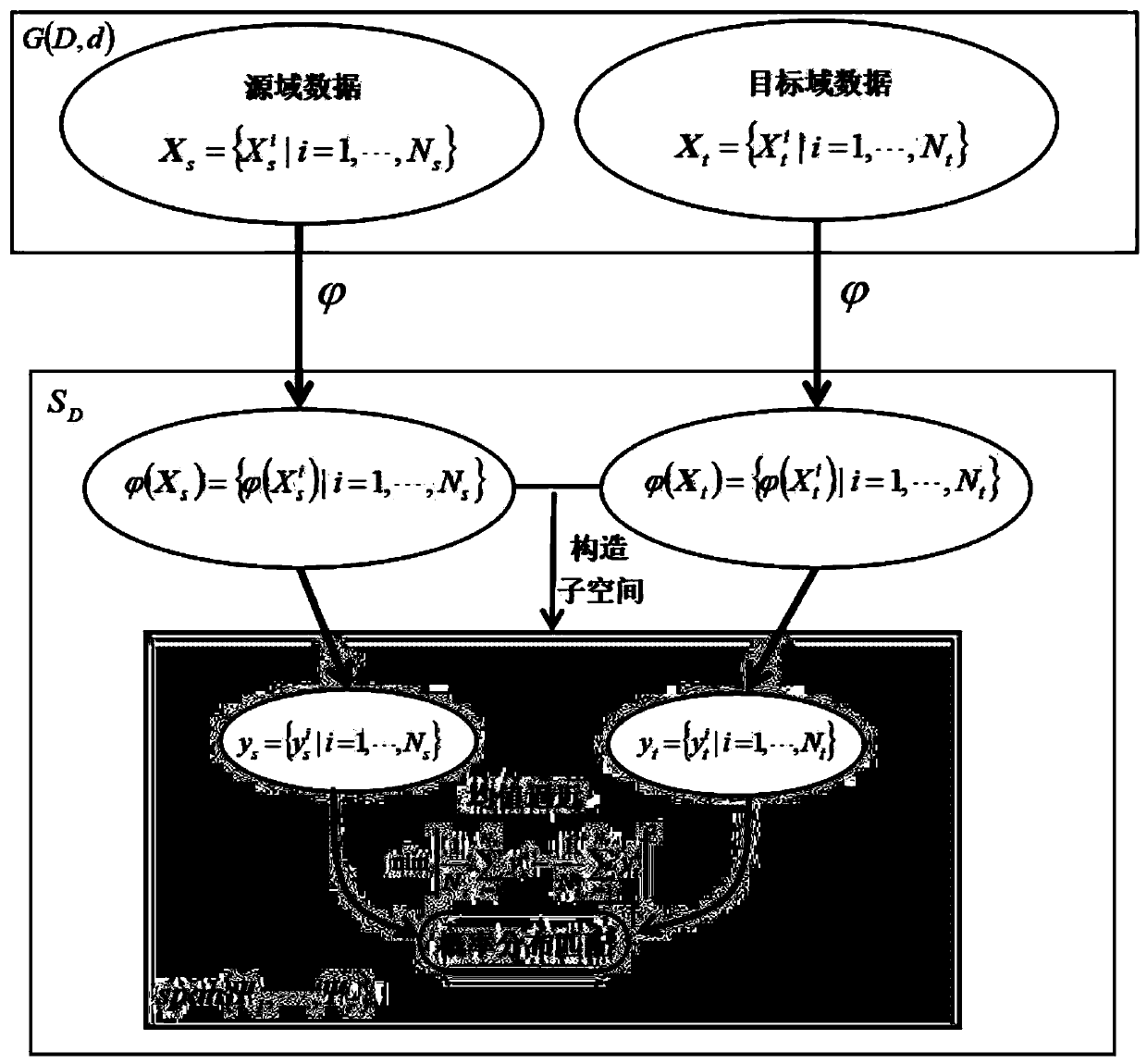
[0021] The present invention aims to provide a domain adaptive method for Grassmannian manifolds. The basic idea is to use the mapping from Grassmannian manifolds to symmetric matrix spaces to transfer Grassmannian manifold data to symmetric matrix spaces, and The subspace is constructed in a symmetric matrix space, and the subspace learning is carried out by using the principle that the projection mean value of the data in the source domain and the target domain is similar in this subspace. The specific principle of the present invention is introduced below.
[0022] make for N s source domain data, for N t Each target domain data, each data is a matrix representation on the Grassmannian manifold G(D,d), that is, each data is a D×d dimensional column vector orthonormal matrix. The symmetric matrix space is denoted as S D , the elements of the symmetric matrix space are D×D dimensional symmetric matrices.
[0023] Build a mapping from a Grassmannian manifold to a symme...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com