Signal compression and recovery method and system based on tensor decomposition and deep learning
A tensor decomposition and signal compression technology, applied in the field of signal processing, can solve the problems affecting the accuracy of signal recovery, slow convergence, and limit the application field of compressed sensing, and achieve the effect of reducing computational complexity and space for computation and storage.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
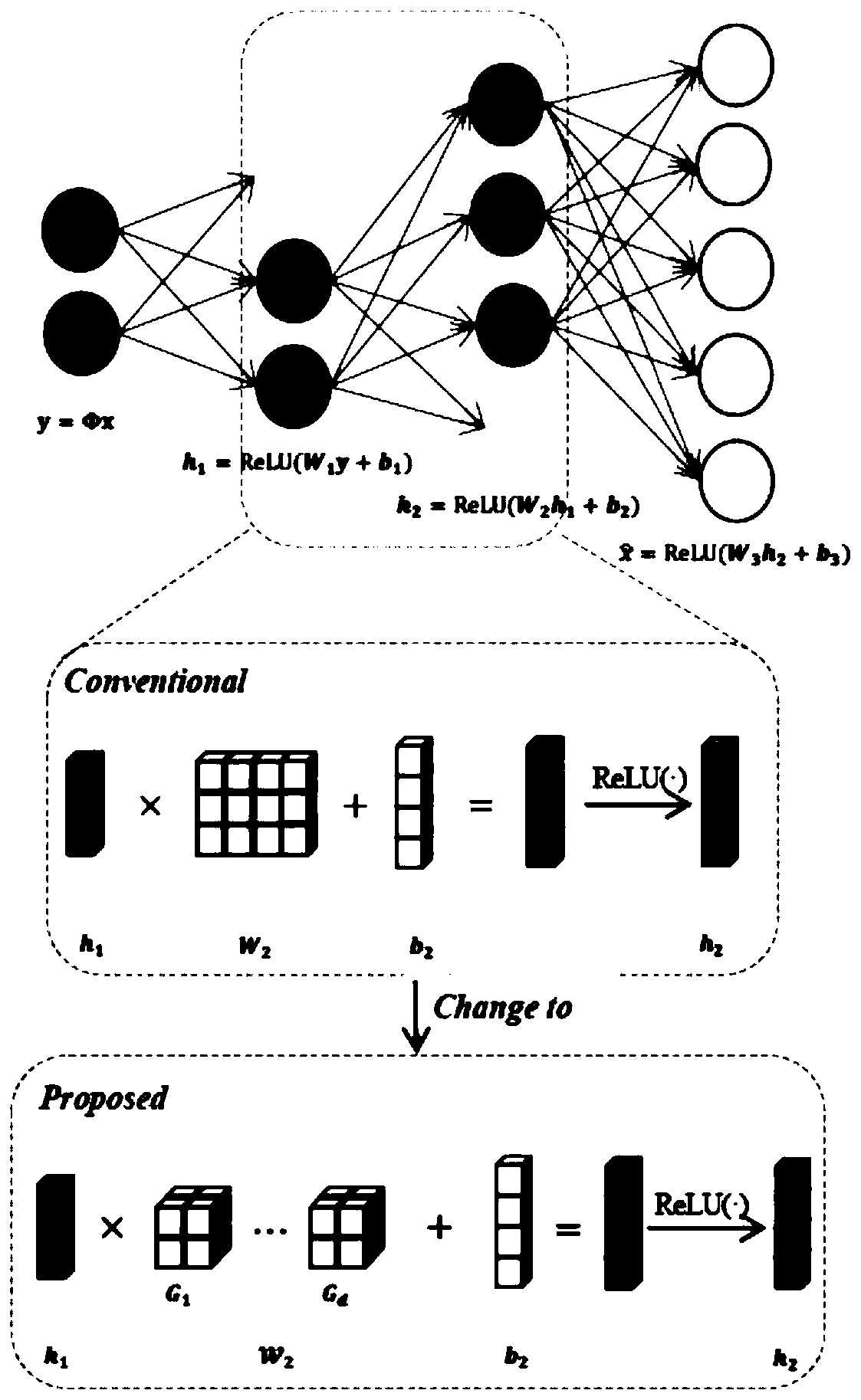
[0056] Such as figure 2 As shown, the embodiment of the present invention is a signal compression and recovery method based on Tensor-Train tensor decomposition and deep learning, the method includes the following steps:
[0057] Step 1, generating a measurement matrix according to a preset signal sampling rate;
[0058] Specifically, the dimension of the original signal is 14400, and the sampling rate is 0.04, that is, the ratio of the dimension of the compressed signal to the dimension of the original signal, and the dimension of the compressed signal is 576. Generate a random Gaussian matrix with a size of 576×14400 and a standard deviation of 0.2, and then orthogonalize its rows to obtain a measurement matrix.
[0059] Step 2, generating a compressed signal;
[0060] Specifically, the measurement matrix is multiplied by the original signal with a dimension of 14400 and the measurement matrix to obtain a compressed signal with a dimension of 576.
[0061] Step 3: Buil...
Embodiment 2
[0092] Such as figure 2 As shown, the embodiment of the present invention is a signal compression and recovery method based on CP tensor decomposition and deep learning, the method includes the following steps:
[0093] Step 1, generating a measurement matrix according to a preset signal sampling rate;
[0094] Specifically, if the dimension of the original signal is 1024 and the sampling rate is 0.25, the dimension of the compressed signal is 256. Generate a random Gaussian matrix with a size of 256×1024 and a standard deviation of 0.2, and then orthogonalize its rows to obtain a measurement matrix.
[0095] Step 2, generating a compressed signal;
[0096] Specifically, the measurement matrix is multiplied by the original signal with a dimension of 1024 and the measurement matrix to obtain a compressed signal with a dimension of 256.
[0097] Step 3: Build a neural network with three fully connected layers, and decompose the weight matrix of the fully connected layer us...
Embodiment 3
[0102] Such as figure 2 As shown, the embodiment of the present invention is a signal compression and recovery method based on Tucker tensor decomposition and deep learning, and the method includes the following steps:
[0103] Step 1, generating a measurement matrix according to a preset signal sampling rate;
[0104] Specifically, if the dimension of the original signal is 14400 and the sampling rate is 0.08, the dimension of the compressed signal is 1152. Generate a random Gaussian matrix with a size of 1152×14400 and a standard deviation of 0.2, and then orthogonalize its rows to obtain a measurement matrix.
[0105] Step 2, generating a compressed signal;
[0106] Specifically, the measurement matrix is multiplied by the original signal with a dimension of 14400 and the measurement matrix to obtain a compressed signal with a dimension of 1152.
[0107] Step 3: Build a neural network with three fully connected layers, and decompose the weight matrix of the fully conn...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com