Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Finite difference multi-resolution trigonometric function WENO format simulation method

A technology of trigonometric functions and finite differences, which is applied in the simulation field of WENO format of finite difference multiple resolution trigonometric functions, and can solve problems such as reduced precision

Pending Publication Date: 2020-02-11
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF1 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Compared with the classic fifth-order finite-difference WENO scheme, the multi-resolution trigonometric WENO scheme solves the problem of waves and high-frequency oscillations by using reconstructed trigonometric polynomials instead of algebraic polynomials as building blocks of the finite-difference WENO scheme. Numerical simulation of compressible flow field problems and low pressure and low density problems, and high-order numerical accuracy can be achieved in smooth areas, and the format accuracy can be continuously reduced near strong discontinuities and maintain the characteristics of basically no oscillation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Finite difference multi-resolution trigonometric function WENO format simulation method
  • Finite difference multi-resolution trigonometric function WENO format simulation method
  • Finite difference multi-resolution trigonometric function WENO format simulation method

Examples

Experimental program
Comparison scheme
Effect test

example 1

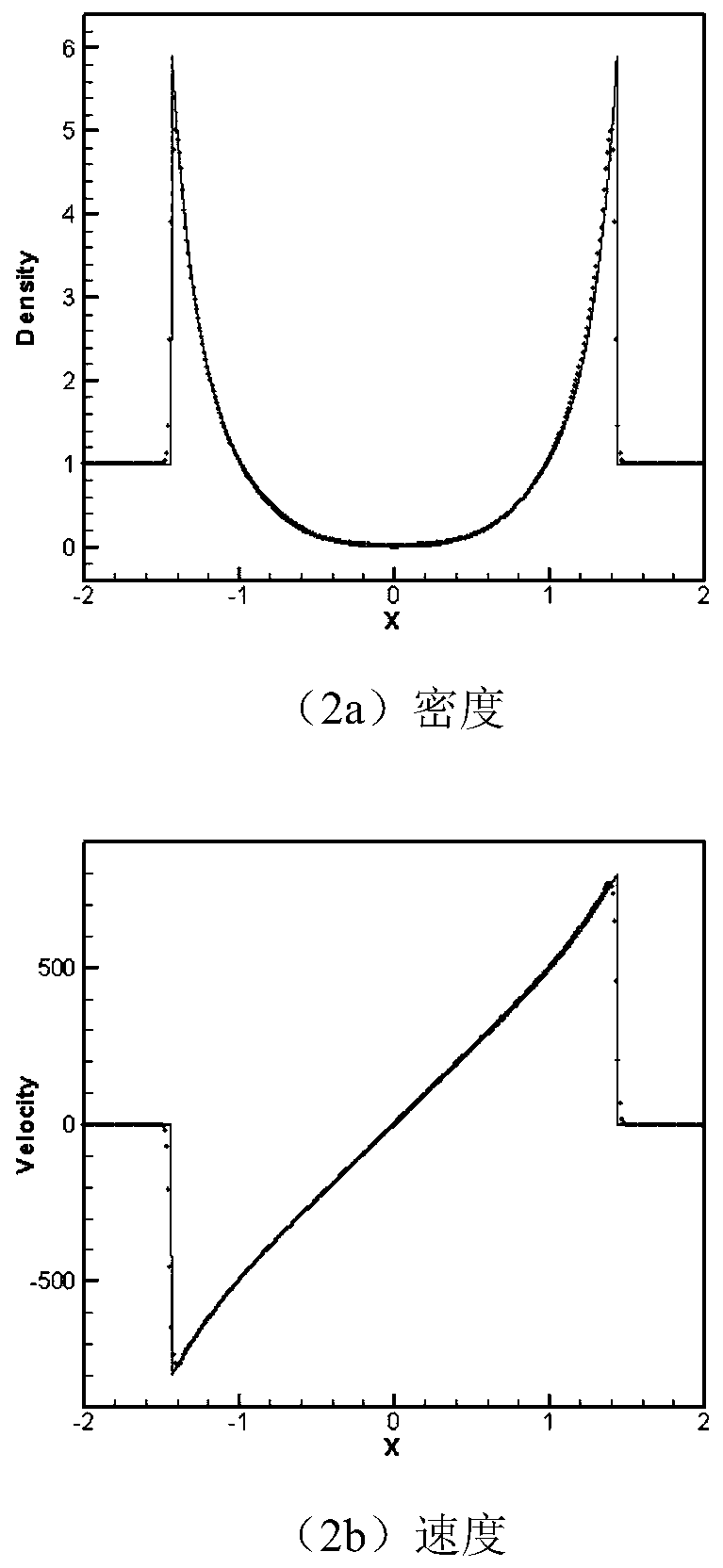
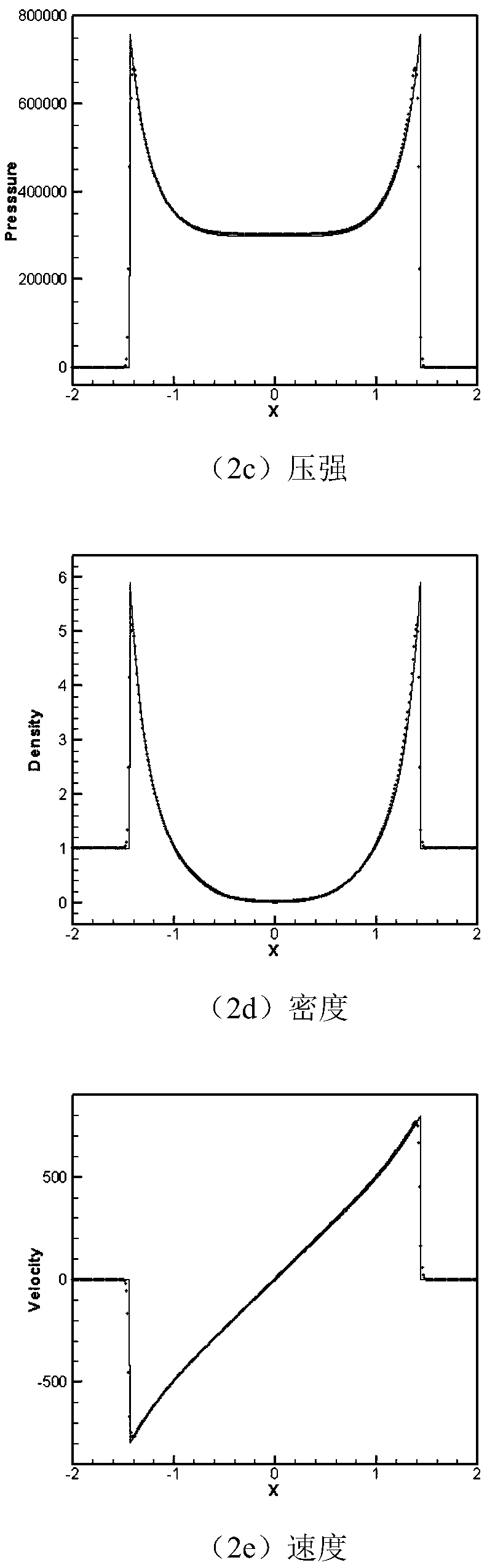
[0144] Example 1. Solving the one-dimensional Euler equation

[0145]

[0146] where ρ is the density, u is the velocity in the x direction, E is the total energy, and p is the pressure. The initial conditions are ① ρ(x,0)=1+0.99sin(x); ②ρ(x,0)=1+0.999sin(x); ③ρ(x,0)=1+0.99999sin(x); and u(x,0)1=, p(x,0)=1, γ=1.4. The calculation area of ​​x is [0,2π], which satisfies the periodic boundary conditions. The exact solution of the density is ① ρ(x,t)=1+0.99sin(x-t); ②ρ(x,t)=1+0.999sin(x-t); ③ρ(x,t)=1+0.99999sin(x-t ). Numerically calculate the solutions when ①t=0.1; ②t=0.01; ③t=0.0001. The classic WENO-JS format does not work for the third case, because the density calculated with it produces negative values. The error and numerical accuracy of the density obtained by numerical simulation using the new finite-difference multiple-resolution trigonometric function WENO scheme and the classical WENO-JS scheme are shown in Tables 1 and 2. Obviously, both the trigonometric func...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a finite difference multi-resolution trigonometric function WENO format simulation method which comprises the following steps: S1, discretizing a hyperbolic conservation law equation into a space semi-discrete ordinary differential equation, and reconstructing a high-order approximation value of numerical flux by adopting a novel finite difference multi-resolution trigonometric function WENO format; S2, adopting a four-order TVB Runge-Kutta time discrete formula to discretize the space semi-discrete finite difference format into a space-time full-discrete high-precisionfinite difference format; S3, obtaining an approximate value on the next time layer according to the space-time full-discrete high-precision finite difference format; and sequentially iterating to obtain a numerical result of the flow field at the termination moment in the calculation area. According to the method, high-precision numerical simulation can be carried out on various compressible flow field problems, especially the low-pressure low-density problem and the high-frequency oscillation problem, numerical simulation of the compressible flow field problems and the low-pressure low-density problem of waves and high-frequency oscillation is achieved, robustness is higher, and the method is easier to popularize to a high-dimensional space.

Description

technical field [0001] The invention relates to the technical field of computational fluid dynamics engineering, in particular to a finite-difference multi-resolution trigonometric function WENO format simulation method. Background technique [0002] It is well known that the multi-resolution format can effectively reduce the numerical computation cost of the high-resolution format and the high-precision format. The solution of the hyperbolic conservation law equation may contain strong discontinuities in small and isolated regions and may be smooth in most of the remaining computational regions. Therefore, the multiresolution technique can focus on regions containing strong discontinuities. The purpose of using the multiresolution technique It is to concentrate the amount of computation on small areas containing strong discontinuities. [0003] On the other hand, numerical methods based on trigonometric polynomials are suitable for simulating high-frequency oscillation pro...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/23G06F30/28G06F111/10G06F113/08
Inventor 王延萌朱君
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com