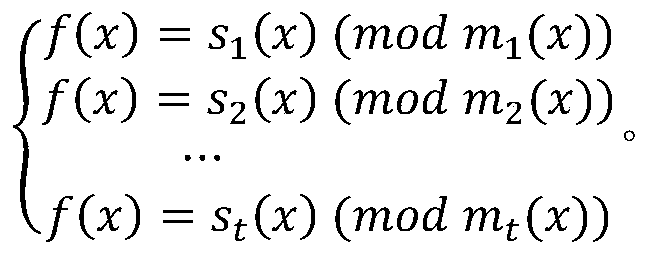Method for realizing secret sharing on non-Euclidean ring by using general coefficient discovery algorithm
A secret sharing and secret technology, applied in transmission systems, digital transmission systems, secure communication devices, etc., can solve the problems of not finding the mode polynomial, difficulty, and modulus difficulty, so as to ensure confidentiality, improve effects, and improve efficiency. Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
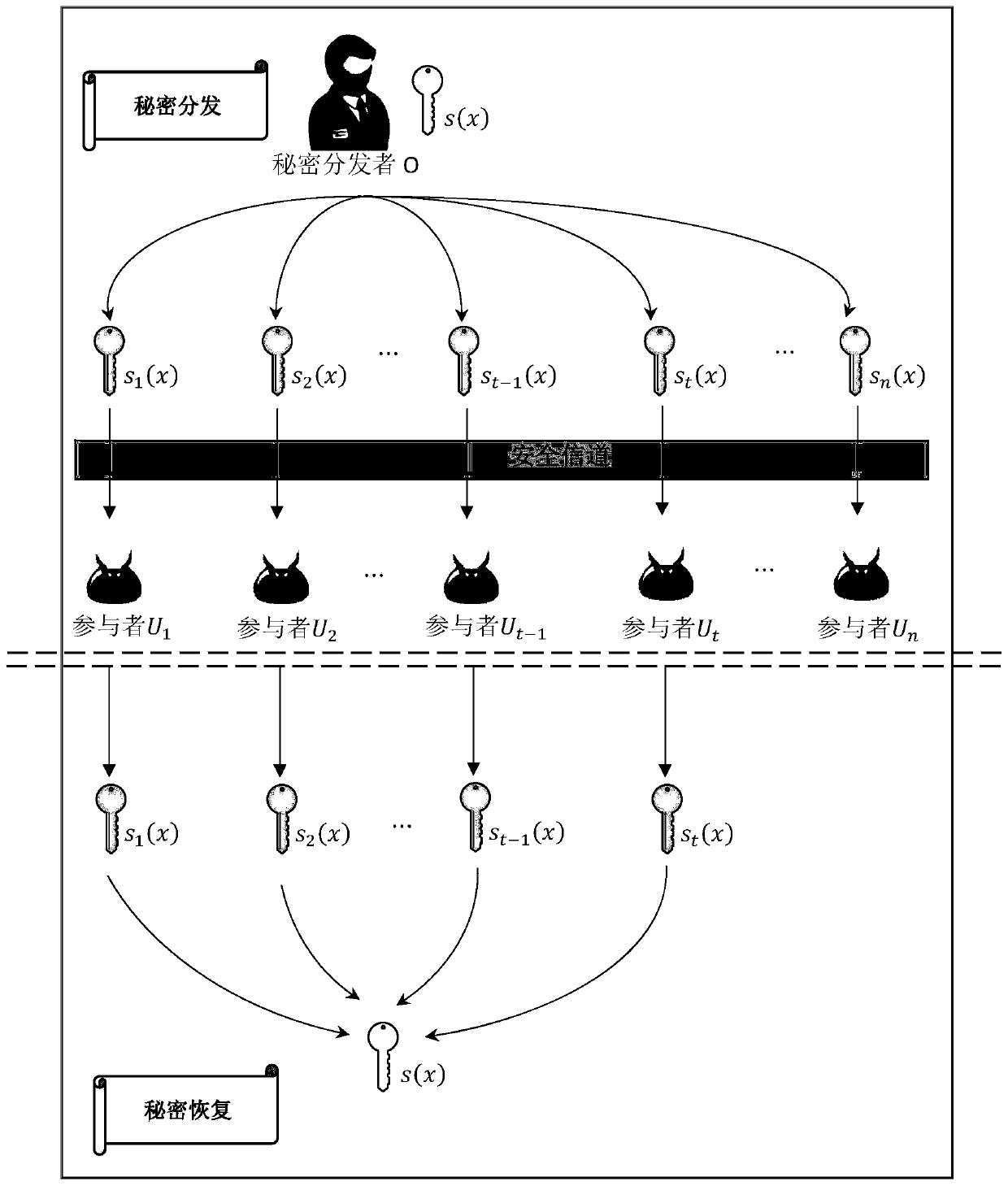
[0066] The technical solutions in the embodiments of the present invention will be clearly and completely described below in conjunction with the accompanying drawings in the embodiments of the present invention. Obviously, the described embodiments are only some of the embodiments of the present invention, not all of them. Based on the embodiments of the present invention, all other embodiments obtained by persons of ordinary skill in the art without making creative efforts belong to the protection scope of the present invention.
[0067] The non-Euclidean ring contains the polynomial ring R[x] as the unique decomposition ring (UFD), R represents various commutative integral rings, and x represents the variable of the polynomial; for example, 3x 2 +2x+5 is a polynomial with x as a variable coefficient on the integer ring Z. Z[x] is a form of polynomial ring R[x], Z represents an integer ring, and Z[x] represents a ring formed by a polynomial whose coefficient is on Z (integer...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com