Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Robust control method based on reinforcement learning and Lyapunov function

A technology of reinforcement learning and robust control, applied in the direction of adaptive control, general control system, control/regulation system, etc., can solve the problems of low safety and stability, to ensure free exploration, high efficiency and safety Effect

Active Publication Date: 2020-03-27
SUN YAT SEN UNIV
View PDF6 Cites 14 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] In order to overcome the problem of low security and stability of the robot control method in the above-mentioned prior art, the present invention provides a robust control method based on reinforcement learning and Lyapunov function, and uses adaptive online Bayesian reasoning to control robot dynamics. Modeling, based on Lyapunov's construction of constrained reinforcement learning problems, to achieve efficient learning, stable work, and safe exploration of robots

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Robust control method based on reinforcement learning and Lyapunov function
  • Robust control method based on reinforcement learning and Lyapunov function
  • Robust control method based on reinforcement learning and Lyapunov function

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

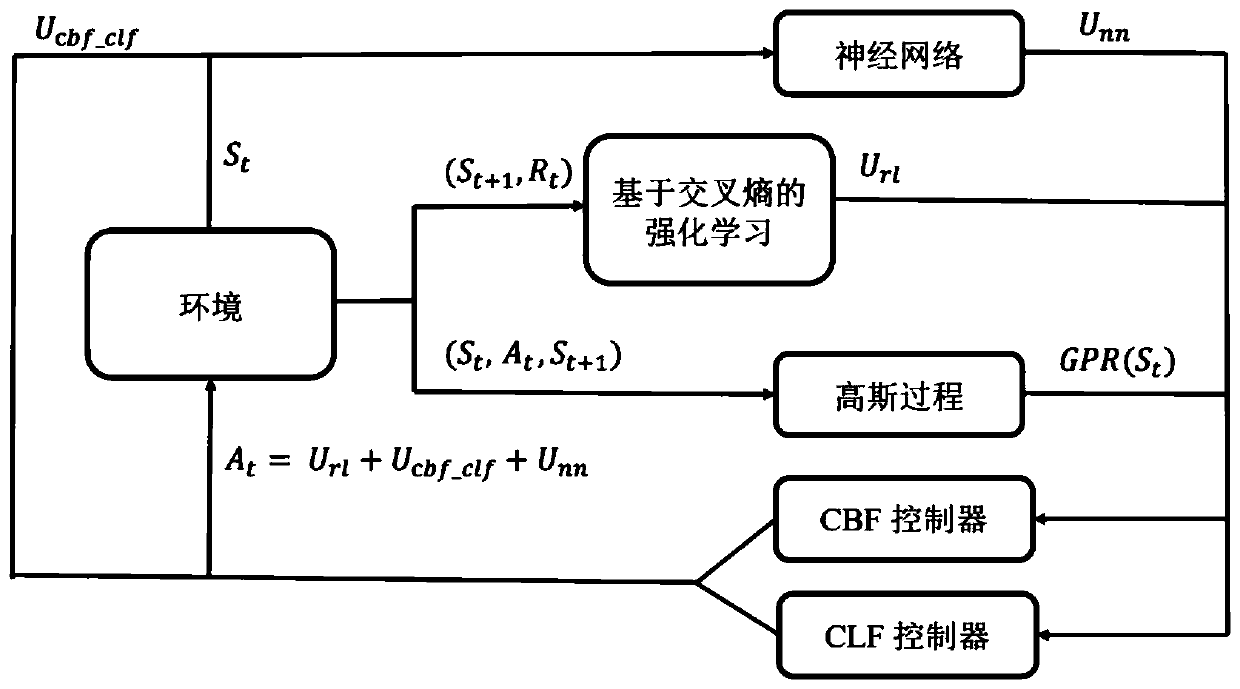
[0038] like figure 1 Shown is an embodiment of a robust control method based on reinforcement learning and Lyapunov functions, including the following steps:

[0039] Step 1: Build an affine system model, and then model the uncertainty in the system dynamics model based on the Gaussian process; the nonlinear affine system can be modeled as: Among them, f(s)+g(s)a represents the prior model obtained by modeling system dynamics and kinematics, and d(s) represents the deviation between the model and the real environment; Gaussian process regression obtains the state s through Bayesian inference * The lower deviation d(s * ) mean and variance:

[0040]

[0041]

[0042] Among them, k(s i ,s j ) is the kernel function defined in GP, ​​k n =[k(s 1 ,s * ), k(s 2 ,s * ),...,k(s n ,s * )], [K] i,j =k(s i ,s j ) is the kernel matrix, is the label vector, σ noise is the standard deviation of label data noise, I is the identity matrix;

[0043] Get a high confiden...

Embodiment 2

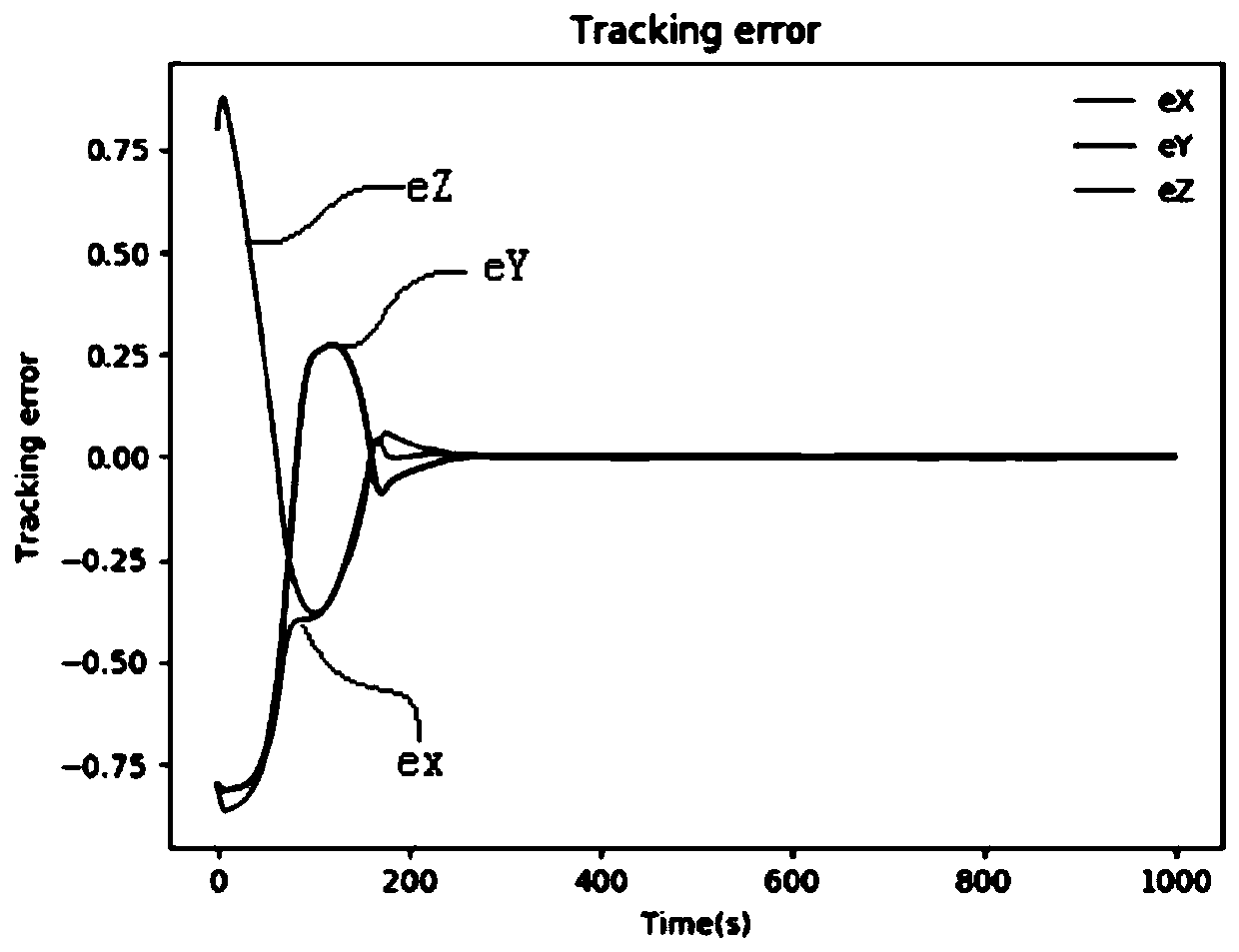
[0060] like Figure 1-3 As shown, on the basis of Embodiment 1, this embodiment takes the trajectory tracking and obstacle avoidance tasks of a quadrotor UAV under random wind field interference as an example to illustrate the specific implementation steps of this method:

[0061] Step 1: In this example, based on the prior knowledge of robot dynamics and the actual task scene, a baseline nonlinear affine system model is established, and a parameterized trajectory in three-dimensional space is set, including the trajectory start point and end point, which is recorded as r(t) ∈ R 3 .

[0062] Define the safe state space of the UAV according to the task scenario: C={x|h(x)≥0} and the target balance point, such as: avoiding obstacles, the trajectory point as the balance point, and designing the corresponding control barrier function (CBF )h(s t ) and the Lyapunov function (CLF) V(s t ).

[0063] Step 2: Select the framework of model predictive control as the benchmark strate...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a robust control method based on reinforcement learning and a Lyapunov function. Modeling is conducted on robot dynamics through self-adaptive online Bayesian reasoning, a constrained reinforcement learning problem is constructed based on Lyapunov, and efficient learning, stable work and safe exploration of the robot are achieved by constructing a Lyapunov function controlstrategy and a barrier function control strategy. The technical problems of insecurity, instability and inefficiency of a nonlinear hybrid dynamic safety-critical robot system facing system uncertainty and external environment uncertainty in a task scene with limited state and action space are solved.

Description

technical field [0001] The invention relates to the field of robot control, and more specifically, to a robust control method based on reinforcement learning and Lyapunov functions. Background technique [0002] With the development of the times, robots play an important role in various fields of modern life, such as intelligent manufacturing, transportation, medical care, emergency rescue and disaster relief, etc. The real world environment has unstructured and dynamic uncertainties. Therefore, in the face of complex robot systems with nonlinear, hybrid dynamic models and limited state and action spaces, in mission scenarios where safety is extremely critical, it is necessary to design an efficient An adaptive controller that is stable and secure at the same time. [0003] In order to achieve the above goals, there are two methods used, one is the optimal control method, and the other is the control method based on reinforcement learning; the optimal control method is to u...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05B13/04
CPCG05B13/027G05B13/042
Inventor 潘杰森郑磊成慧胡海峰
Owner SUN YAT SEN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com