Supercharge Your Innovation With Domain-Expert AI Agents!

Cubic root solving device and method based on hyperbolic CORDIC

A cube root, to-be-solved technology, applied in the field of cube root solving devices based on hyperbolic CORDIC, to achieve the effect of small hardware resource consumption, short critical path, and fast calculation speed

Pending Publication Date: 2020-11-24
NANJING UNIV
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The algorithm was proposed in 1959, at first it could only be used to calculate trigonometric functions and multiplication and division

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Cubic root solving device and method based on hyperbolic CORDIC
  • Cubic root solving device and method based on hyperbolic CORDIC
  • Cubic root solving device and method based on hyperbolic CORDIC

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

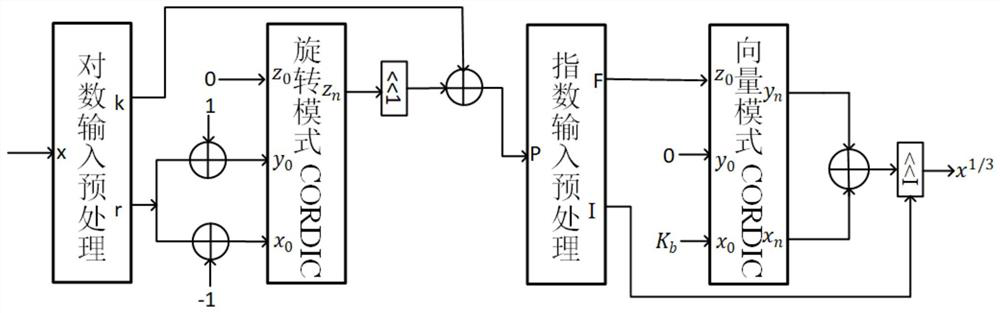
[0050] (1) In this embodiment, the input data is [10 -6 , 10 6 ]. The input and output bit widths of each computing module and main logic unit are as follows:

[0051] Table 1 Input and output bit width table

[0052]

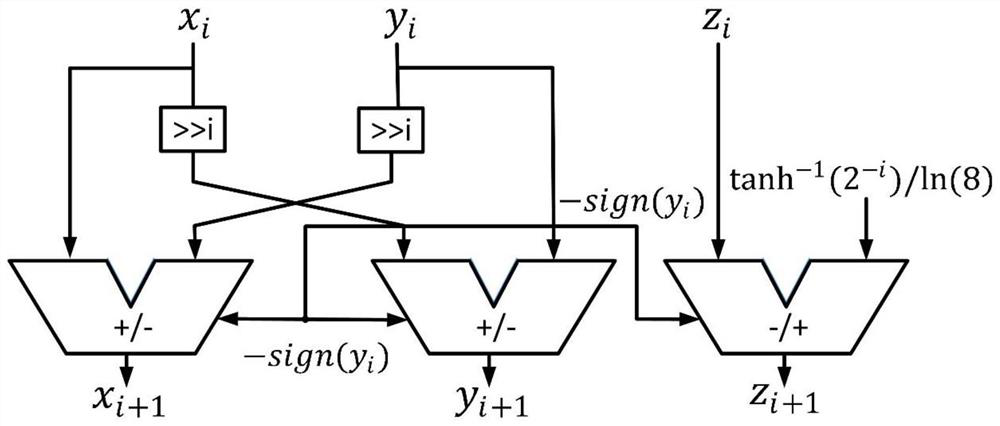
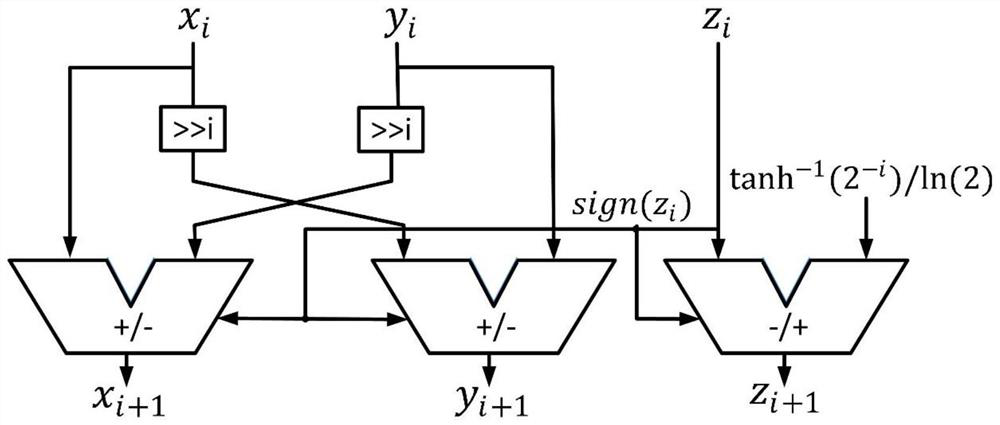
[0053] In the CORDIC algorithm, the maximum iteration number is set to 20, and the number 4 and 13 need to be iterated once, so a total of 22 iterations are required. According to the empirical formula, the decimal place width of the input should be bit. Therefore, the fractional bit width is set to 27 bits. because So the integer bit width of the input is set to 20 bits. In the logarithmic input preprocessing module, since the maximum number of inputs is 8 6 6 7 , therefore, the maximum value of k is 6, requiring 3 bits.

[0054] In the CORDIC algorithm under the vector mode generalized hyperbolic coordinate system, the maximum iteration number is set to 20, and the logarithm is input to the output r of the preprocessing module. output as beca...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a cubic root solving device and method based on hyperbolic CORDIC. According to the method, cubic root calculation is converted into logarithm and exponent which can be calculated through a CORDIC algorithm under a generalized hyperbolic coordinate system. The device is characterized in that a logarithm input preprocessing module converts any positive number x into 8k*r, alogarithm calculation module is used for calculating a hyperbolic arc tangent value based on 8 through a generalized hyperbolic CORDIC calculation unit working in a vector mode, and then obtaining a logarithm index through shifting and adding operations, and splitting the logarithm index preprocessing module into an integer part I and a decimal part F, and an index calculation module is used for solving a hyperbolic sine value and a hyperbolic cosine value based on 2 through a generalized hyperbolic CORDIC calculation unit working in a rotation mode so as to obtain an index 2F through additionoperation and shift leftwards by I bits to obtain a calculation result. Only simple logic units such as addition and shifting are adopted, and the method has advantages of short critical path, low hardware overhead and the like.

Description

technical field [0001] The invention relates to the field of digital signal processing of VLSI, in particular to a hyperbolic CORDIC-based cube root solving device and solving method. Background technique [0002] Cube root is widely used in scenarios such as spectrum analysis, audio signal processing, digital communication and 3D image technology. Many scholars have made contributions to the circuit design of the cube root. The most common method for finding cube roots is Newton's iterative method. The Newton iterative method converges quickly. However, an initial guess value is required when solving, and the guess value has a relatively large impact on the accuracy. Moreover, the Newton iterative method requires a large number of multiplication operations, which consumes a lot of hardware resources. Numerical recursion is a new method of solving cube roots, but this method also cannot avoid the heavy use of multipliers. [0003] Because the CORDIC algorithm only has s...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F7/556G06F7/575
CPCG06F7/556G06F7/575Y02D30/70
Inventor 潘红兵安梦瑜王宇宣
Owner NANJING UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com