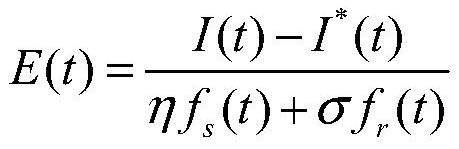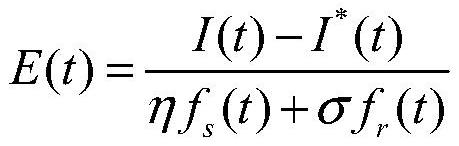Optimal intervention simulation method and system for panic emotion in crowd evacuation

[0044]Example one:

[0045]The purpose of this embodiment is to provide an optimal intervention simulation method for panic in crowd evacuation.

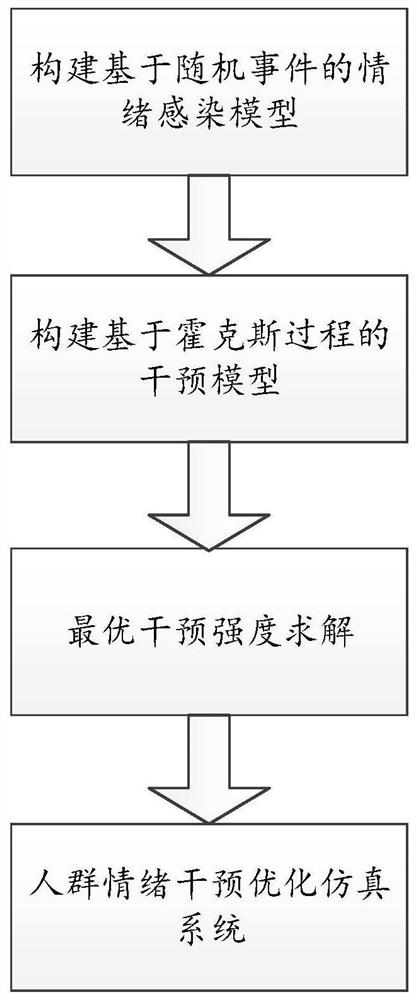
[0046]Such asfigure 1 As shown, an optimal intervention simulation method for panic in crowd evacuation includes:

[0047]Step 1: Establish an emotional infection model (SEEC) based on random events to analyze the process of crowd emotional infection;

[0048]Step 2: Establish an intervention model based on the Hawkes process (HIEC), which can adaptively adjust the intervention intensity according to the changes in the intensity of the population event;

[0049]Step 3: Propose a problem of the maximum rate of return, and use the artificial bee colony optimization algorithm to intervene in emotional infection (IE-ABC) to obtain the optimal solution. According to the current individual's collision-free speed, perform crowd evacuation simulation movement;

[0050]Step 4: According to the current emotional intervention measures, perform the optimal intervention simulation of panic emotion during crowd evacuation.

[0051]In the step 1, the construction of the emotional infection model based on random events includes: building the event occurrence intensity and state transition matrix, wherein the event occurrence intensity needs to calculate the infection rate and recovery rate in the population, which is mentioned in this article The infection rate β and recovery rate γ reached, and the number of emotionally infected and susceptible persons in the current population, and the total number of people in the current population; use the infection rate, recovery rate, number of infections, number of susceptible people, and total number of people to find the infection event The intensity of occurrence and the intensity of recovery events. Specifically, the intensity of the incident is first constructed, and S is defined as the emotionally susceptible person, I is the emotionally infected person, the emotionally infected person infects the surrounding susceptible individuals, and the infected person can return to a normal state and become a normal individual. The individual still has the probability of being infected again; the infected person is in the infected state, and the susceptible person is in the normal state. Whenever a susceptible person enters the infected state, it is said that an infection event has occurred. Whenever an infected person enters a normal state, we Said that a recovery event occurred.

[0052]The SIS model divides the population into two categories, S stands for susceptible persons and I stands for infected persons. In the SIS model, S has a probability of being infected to become I, and I has a probability of reverting to S. S(t) and I(t) represent the number of people in S and I, respectively, at time t. At any given time t, S(t) and I(t) take integer values; we assume that the value of Δt is small enough that the number of individuals can change at most 1 within the time interval of Δt, that is, only from the state {I( t)=i} to {I(t+Δt)=i+1} corresponds to a new emotional infection, or from the state {I(t)=i} to {I(t+Δt)=i+1} Corresponds to emotional recovery, or the number remains unchanged, which results in:

[0053]

[0054]Pr{dE(t)=1,dI(t)=1|T(t)}, Pr{dE(t)=0,dI(t)=-1|T(t)}, Pr{dE(t )=0, dI(t)=0|T(t)} respectively represent the probability of only one emotional infection event under the historical condition of T(t), and only once under the historical condition of T(t) The probability of an emotional recovery event, under the historical conditions of T(t), the probability that an event did not occur, β represents the effective number of infected individuals per unit time, and γ is the recovery rate per unit time. Here we construct an event-based The emotional infection model, the intensity of infection events and recovery events are as follows:

[0055]

[0056]ψR(t)=γI(t) (3)

[0057]The meaning of the formula for the intensity of emotional infection events: β is the infection rate, βI(t) represents the sum of the number of infected individuals per unit time (at time t) that can be effectively infected, Indicates the proportion of susceptible individuals in the population at time t, and the multiplication of the two represents the number of people who are effectively infected with normal individuals, that is, the number of people infected per unit time; the meaning of the intensity of the recovery event: γ is the unit time Recovery rate, γI(t) represents the number of people returning to normal per unit time.

[0058]Secondly, construct the state transition matrix, set the number of people as N, define G(I,S,t)={i,j} as the state of the crowd, and N=i+j, which means that there are i infections in the crowd at time t And j normal individuals; at the beginning of emotional infection, the initial state of the population is defined as G(I, S, t0)={i,j}; Let Δt be a time interval small enough, within this time interval, only one event can occur, there is a certain probability that an infection event will occur, and there is a certain probability that an emotional recovery event will occur; if it occurs once Infection event, the state of the crowd will change from {i,j} to {i+1,j-1}, if a recovery event occurs, the state of the crowd will change from {i,j} to {i-1,j +1}, if no event occurs, the state remains unchanged; define D as the state space of the crowd, D={(i,j)|0≤i≤N,0≤j≤N}, that is, the two most extreme crowds The statuses {i, 0} and {0, j} respectively indicate that all the population has become emotionally infected and all the population has become normal individuals.

[0059]From the intensity of the infection event and the intensity of the recovery event obtained before, we get the following state transition probability:

[0060]

[0061]Here we stipulate s=N-i, P(i, j) (Δt) represents the probability of changing from state i to state j within the time interval Δt, and the probability that the state {i} becomes {i+1} within the time interval Δt is The probability that the state becomes {i-1} is γIΔt, and the probability that the state remains unchanged is The state of I ranges from 0 to N. Here, a matrix of (N+1)(N+1) scale is used to represent the state transition matrix. According to the above state transition probability, we can get the state transition matrix in a time interval Δt:

[0062]

[0063]The row and column subscripts of the matrix all start from 0 to N. The subscript of a two-dimensional matrix indicates the form of state transition. For example, the subscript 00 in the matrix represents the transition from state {I=0} to state {I=0}. 12 represents the transition from state {I=1} to state {I=2}, P(i, j) (Δt) represents the probability of transition from state {I=i} to state {I=j}.

[0064]Furthermore, by deriving from the above formula, we get a complete state transition matrix of crowd emotional infection. When we get an initial scene, we can define its initial state. According to the state transition matrix, we can get every subsequent time Changes in the number of emotionally infected persons in the step scene. This article defines p(t)=(p0(t),p1(t),p2(t)....pN(t),)TIs the state vector at time t, pi(t) is the probability of I(t)=i at time t, i∈[0,N].

[0065]p(Δt)=P(Δt)p(0) (6)

[0066]p(t+Δt)=P(Δt)p(t)=Pn+1(Δt)p(0) (7)

[0067]Among them, p(0) represents the initial state. Here we define t=nΔt. At the initial moment of the spread of emotions, we are given a state vector about the infected person in the current scene. For example, p(0)=(0,0,0...1...0,0), we can calculate the probability of I(t)=i at any time according to the above state transition matrix, i∈[0, N]. From this we can get the changes in the state of the emotionally infected person in the scene, and then analyze the real-time situation of the spread of emotion in the scene.

[0068]In the step 2, the construction of the intervention model includes:

[0069]In order to control the emotional infection in the crowd, we have proposed a control measure against emotional infection. The intervention strategy is divided into two parts. The first part is to reduce the infection capacity of the infected person, thereby reducing the infection rate β in the population, and the second part is to add artificial treatment to help the emotionally infected people calm down as soon as possible and improve the population recovery rate γ. We use fsAnd frIndicates the strength of the two control strategies respectively. For the two control intensities, we use the point process to model, and we choose the Hawkes process to model our control intensity.

[0070]

[0071]

[0072]fs(t) and fr(t) respectively represent the artificially applied isolation strength and healing strength μ at time t1And μ2Respectively represent the intensity of basic influence. θ1And θ2The attenuation factor representing the isolation intensity and the healing intensity, respectively, means that the impact of historical isolation events and historical healing events on future isolation events and healing events will gradually decrease as time increases, ω1And ω1Is the zoom factor, which indicates the zoom ratio of the impact of the isolation event and healing event that has occurred on the current event. We regulate the infection rate β and cure rate γ of the emotional infection model according to the above two control measures. From this we get:

[0073]β*(t+Δt)=β(t)-fs(t) (12)

[0074]γ*(t+Δt)=γ(t)+fr(t) (13)

[0075]β(t) and γ(t) respectively represent the infection rate and recovery rate of the population at time t, β*(t+Δt) and γ*(t+Δt) respectively represent the new infection rate and recovery rate in the population at t+Δt after the intervention measures are added. From this we get the state transition matrix P after adding the control model*(Δt).

[0076]

[0077]In the same way, we can get the formula of population status transfer after joining intervention measures.

[0078]p(Δt)=P*(Δt)p(0) (15)

[0079]p(t+Δt)=P*(Δt)p(t)=P*n+1(Δt)p(0) (16)

[0080]The step 3, using the artificial bee colony optimal intervention emotional infection algorithm (IE-ABC) to solve the optimal intervention intensity, including:

[0081]First of all, the solution of the intervention intensity is transformed into an optimization problem. Intuitively speaking, if we want to achieve the most ideal control effect, we can increase our intervention intensity as much as possible. The greater the intervention intensity, we can achieve the control effect. Bigger. However, there is a cost issue in real life. We invest too high intervention costs, which may cause a waste of resources. We hope to achieve the best results between the number of infected people and the cost of input. The result we most look forward to is that the intensity of control we invest can control the largest number of infected people and produce the least cost. In this article, the difference in the number of infected people before and after control is taken as the income obtained from the control in this article. The income function is shown below.

[0082]G(t)=I(t)-I*(t) (17)

[0083]I(t) represents the number of emotionally infected people at time t when no control strategy is added, I*(t) represents the number of emotionally infected people at time t after joining the control strategy, and G(t) is the instantaneous return of the control strategy at time t. After joining the control, we have to pay the cost of the two control strategies used. The cost function is shown below.

[0084]C(t)=ηfs(t)+σfr(t) (18)

[0085]C(t) represents the cost of taking two control measures at time t, where η represents the cost of isolating a unit individual, and σ represents the cost of curing a unit individual. The optimal control strategy we propose is to maximize revenue and minimize costs as much as possible, so we define a rate of return to measure the effect of our optimization. The form of rate of return is shown below.

[0086]

[0087]

[0088]E(t) represents the rate of return of our optimization strategy at time t. We solve the optimal parameters of the intervention intensity to optimize the intervention intensity and maximize the rate of return. Below is the definition of our optimization problem.

[0089]

[0090]

[0091]ψR(t)=γI(t)

[0092]I(0)=i

[0093]S(0)=N-i

[0094]μ1(t),κ1(t),θ1(t), μ2(t),κ2(t),θ2(t)>0 (21)

[0095]Among them, μ1*(t),κ1*(t),θ1*(t), μ2*(t),κ2*(t),θ2*(t) represents the optimal parameter of intervention intensity solved at time t, E*(μ1*(t),κ1*(t),θ1*(t), μ2*(t),κ2*(t),θ2*(t)) represents the optimal rate of return at time t.

[0096]Further, the present disclosure proposes an algorithm for controlling emotional infection based on the optimization intervention intensity of artificial bee colonies. The algorithm is used to solve the optimization problem proposed above. Initialization must be performed at the initial stage of the algorithm, including determining the population number, The maximum number of iterations controls the parameter limit. And randomly generate an initial solution in the initial space, xi(i=1,2,3,……,SN), SN is the number of food sources, each solution xiIs a 6-dimensional vector, xij (j = 1, 2, 3, 4, 5, 6) represents one of the six parameters of the intensity of our manual intervention, using xiWe can determine the strength of a candidate intervention; we define fit as the fitness value, and we bring these candidate solutions into the objective function to calculate the fitness value of the candidate solution, and record the solution in the maximum fitness, fitiIndicates the fitness value of the i-th solution, in the form shown below.

[0097]

[0098]Next, the bee colony enters the search stage, leading the bee to find a new solution near the known solution, record it, calculate its fitness value, and search for a new solution formula as shown below.

[0099]wij = Xij +φij (xij -xkj) (twenty three)

[0100]k∈﹛1,2,...,SN﹜,j∈{1,2,...,D}, and k≠i; φij It is a random number between [-1,1]. Calculate the new solution and solve the fitness value of the solution, if the fit of the new solutioniBetter than the old solution, it leads the bee to remember the new solution and forget the old solution. Otherwise, it will retain the old solution. After all the leading bees have completed the search process, the leading bees will dance in the recruitment area to share the solution information and information with the follow bees. Follow the bee to calculate the selection probability of each solution for selection. The calculation formula proposed in this paper is as follows.

[0101]

[0102]PriIs the selection probability of the i-th solution, fitiIs the fitness value of the i-th solution, Represents the cumulative sum of fitness values ​​of all current solutions. Then randomly generate a number in the interval [-1,1], if PriIs greater than the random number, then follow the bee to generate a new solution from Equation 18, and check the new solution, if the fit of the new solutioniIf it is better than before, the follower will remember the new solution and forget the old solution; otherwise, it will keep the old solution. If PriIf it is less than the random number, no new solution will be generated. Finally if the solution xiIf there is no improvement in a predetermined number of iterations, the corresponding lead bee i abandons the solution and becomes a scout bee. When the number of iterations reaches the maximum, the algorithm stops. The algorithm can be executed multiple times to improve the robustness of the algorithm.

[0103]The following is the algorithm for controlling emotional infection based on the optimized intervention intensity of artificial bee colony in this disclosure:

[0104]

[0105]Embodiment two:

[0106]The purpose of this embodiment is to provide an optimized intervention simulation system for panic in crowd evacuation.

[0107]An optimized intervention simulation system for panic in crowd evacuation, including:

[0108]Data collection module, which is used to obtain crowd evacuation process data and determine the intensity of the incident;

[0109]The model building module is used to construct an emotional infection model based on random events, and quantify the process of crowd emotional infection according to the intensity of the event; construct an intervention model based on the Hawkes process, through which the intervention model is used according to the occurrence of crowd events The intensity changes adaptively adjust the intervention intensity;

[0110]The optimization solution module is used to construct a cost objective function for panic emotion optimization, and use the artificial bee colony optimal intervention emotional infection algorithm to solve the optimal intervention intensity, and perform crowd evacuation simulation exercises according to the current individual's collision-free speed.

[0111]Example three:

[0112]This embodiment also provides an electronic device, including a memory and a processor, and computer instructions stored in the memory and running on the processor. When the computer instructions are executed by the processor, the above-mentioned panic during the evacuation of the crowd is completed. Simulation methods for optimal intervention of emotions include:

[0113]Construct an emotional infection model based on random events, and quantify the process of crowd emotional infection according to the intensity of the event;

[0114]Constructing an intervention model based on the Hawkes process, through which the intervention model is used to adaptively adjust the intervention intensity according to changes in the intensity of crowd events;

[0115]Construct a cost objective function for panic emotion optimization, and use the artificial bee colony optimal intervention emotional infection algorithm to solve the optimal intervention intensity, and perform crowd evacuation simulation exercises according to the current individual's collision-free speed.