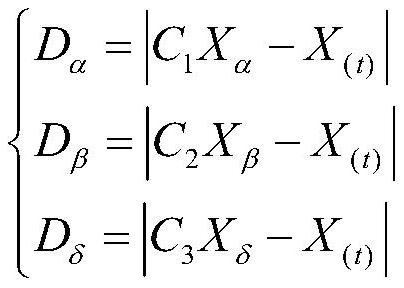Random forest and grey wolf optimized coal body gas content prediction method
What is Al technical title?
Al technical title is built by PatSnap Al team. It summarizes the technical point description of the patent document.
A gas content, random forest technology, applied in forecasting, random CAD, neural learning methods, etc., can solve problems such as unsatisfactory performance, single algorithm, single, etc., to make up for poor performance and improve prediction accuracy.
Pending Publication Date: 2021-02-19
LIAONING TECHNICAL UNIVERSITY
View PDF0 Cites 0 Cited by
Summary
Abstract
Description
Claims
Application Information
AI Technical Summary
This helps you quickly interpret patents by identifying the three key elements:
Problems solved by technology
Method used
Benefits of technology
Problems solved by technology
[0005] Following the traditional prediction methods, many scholars began to use machine learning algorithms for coal gas prediction; related algorithms include support vector machine algorithm and its variants, such as least squares support vector machine algorithm, and BP neural network and Optimized BP neural network, such as using optimization techniques such as fuzzy mathematical algorithm and genetic algorithm to optimize BP neural network; previous studies mostly use a single machine learning algorithm or use optimization technology combined with machine learning algorithm to optimize the coal gas content. For prediction, the algorithm is single, and the disadvantage of the traditional single machine learning algorithm is that it can only get a model with a preference, that is, the performance in some aspects is better, and the performance in other aspects is not satisfactory. Therefore, based on integration The learned coal gas content prediction algorithm came into being
Method used
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more
Image
Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
Click on the blue label to locate the original text in one second.
Reading with bidirectional positioning of images and text.
Smart Image
Examples
Experimental program
Comparison scheme
Effect test
Embodiment 1
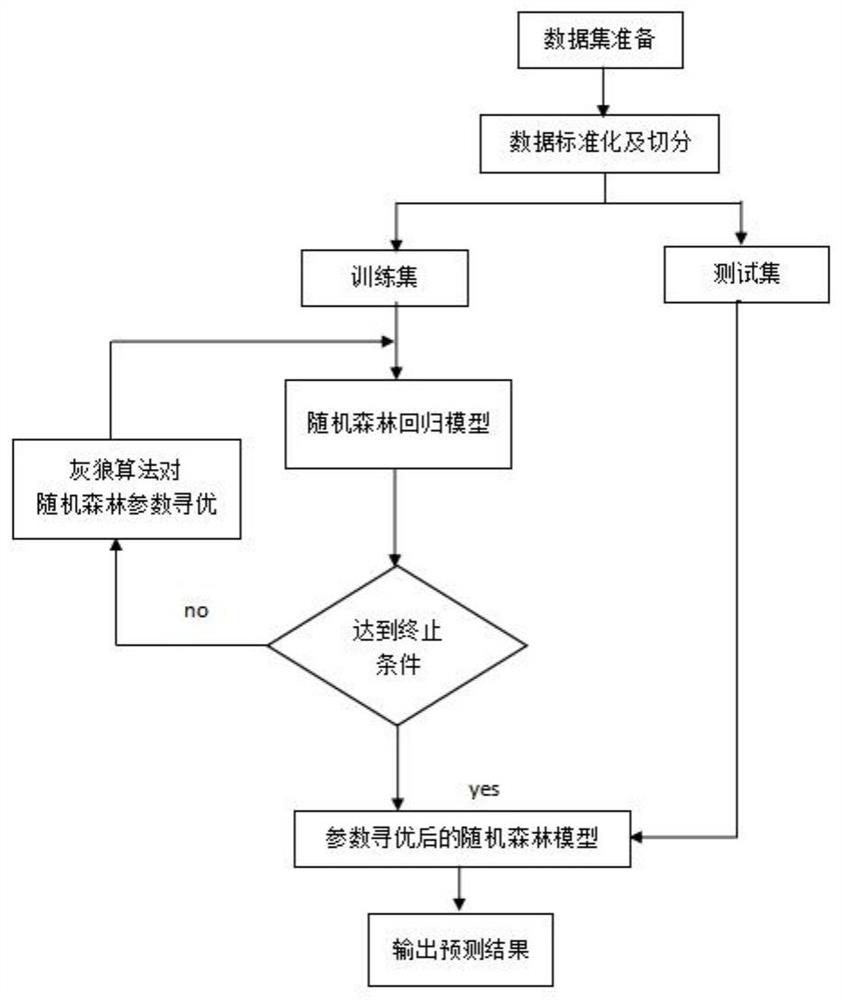
[0034] Embodiment 1: as figure 1 Shown is a flow chart of the gray wolf optimized random forest gas prediction model of an embodiment of the present invention. This embodiment provides a coal gas content prediction method of gray wolf optimized random forest. The specific steps are as follows:
[0035] 1) Receive the measured coal gas content data;
[0036] 2) Perform data preprocessing on missing values of basic data, including filling missing values and feature selection;
[0037] 3) Send the preprocessed data into the random forest prediction model;
[0038] 4) The random forest algorithm adopts bootstrap re-sampling technology to repeatedly randomly extract K sub-data sets from the original training sample set with replacement to form a training sample set, expressed as θ 1 ,θ 2 ... θ K . K sub-datasets generate K decision trees, expressed as T(X,θ 1 ),T(X,θ 2 )...T(X,θ K ). The decision tree grows freely from the root node down without pruning. K decision tr...
Embodiment 2
[0045] Embodiment 2: In this embodiment, the feature selection and gray wolf optimization algorithm appearing in Embodiment 1 are explained in detail.
[0046] (1) Feature selection. First, for each decision tree in the random forest, use the corresponding out-of-bag data to calculate its out-of-bag error, so that K decision trees can get K out-of-bag errors, which are represented by error1. Then add noise interference to the feature X of all out-of-bag data samples, and then calculate its out-of-bag data error. Similarly, K decision trees get K out-of-bag errors, which are represented by error2. The calculation formula for the importance of the final feature X is:
[0047] im=∑(error2-error1) / K
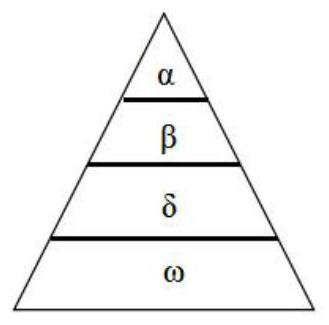
[0048] (2) The process of the gray wolf optimization algorithm is as follows: Initialize the wolf group, and the positions of the gray wolves obey the uniform distribution, that is, X ij ~U[a,b], where a and b are the upper and lower bounds of the uniform distribution interval resp...
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more
PUM
Login to view more
Abstract
The invention discloses a random forest and grey wolf optimized coal body gas content prediction method, which comprises two stages, namely construction of a random Sendor prediction model and use ofa grey wolf optimization algorithm, and aims to select and determine optimal values of relevant parameters of the random forest prediction model by using the grey wolf optimization algorithm. Therefore, the identification and prediction effects of the media gas content prediction model are enhanced. The gas basic data is initialized through two steps of missing value filling and feature selection.The geological characteristics of the coal bodies in different regions are different, and the characteristic selection can be used for carrying out targeted selection on the mine coal body data in different regions, so that the gas content prediction accuracy is enhanced, and the method is suitable for mines in different regions. According to the method, effective prediction of the gas content can be achieved, the working efficiency is improved, meanwhile, implementation of gas disaster prevention measures in the coal mining process can be guided, and the method has important significance inprevention and control of gas disaster accidents and accurate mining of coal.
Description
technical field [0001] The invention relates to the field of coal gas content prediction, in particular to a coal gas content prediction method based on random forest and gray wolf optimization. Background technique [0002] The gas content of the coal seam is an important parameter for the prevention and control of coal mine gas, and it is an important basis for the prediction of mine gas emission and safety control. Building an effective coal seam gas content prediction model can realize accurate assessment of gas content and guide the implementation of gas disaster prevention measures in the coal mining process, which is of great significance for the prevention and control of gas disaster accidents and precise coal mining. However, the prediction of coal gas content is time-consuming and labor-intensive, so it is necessary to develop a coal gas content prediction method to improve the prediction accuracy of gas content. [0003] At present, there have been a series of st...
Claims
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more
Application Information
Patent Timeline
Application Date:The date an application was filed.
Publication Date:The date a patent or application was officially published.
First Publication Date:The earliest publication date of a patent with the same application number.
Issue Date:Publication date of the patent grant document.
PCT Entry Date:The Entry date of PCT National Phase.
Estimated Expiry Date:The statutory expiry date of a patent right according to the Patent Law, and it is the longest term of protection that the patent right can achieve without the termination of the patent right due to other reasons(Term extension factor has been taken into account ).
Invalid Date:Actual expiry date is based on effective date or publication date of legal transaction data of invalid patent.
Login to view more 
Login to view more