Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

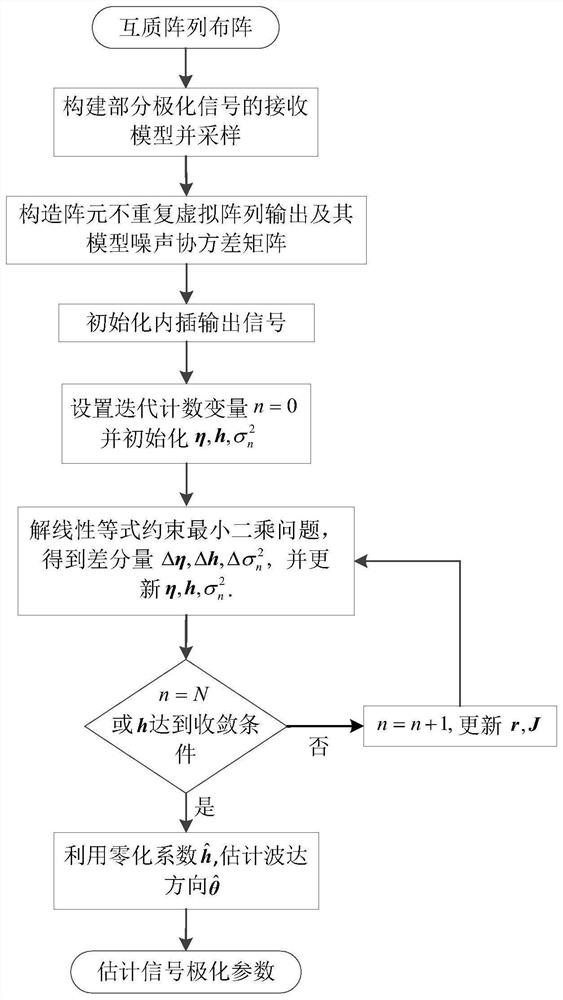
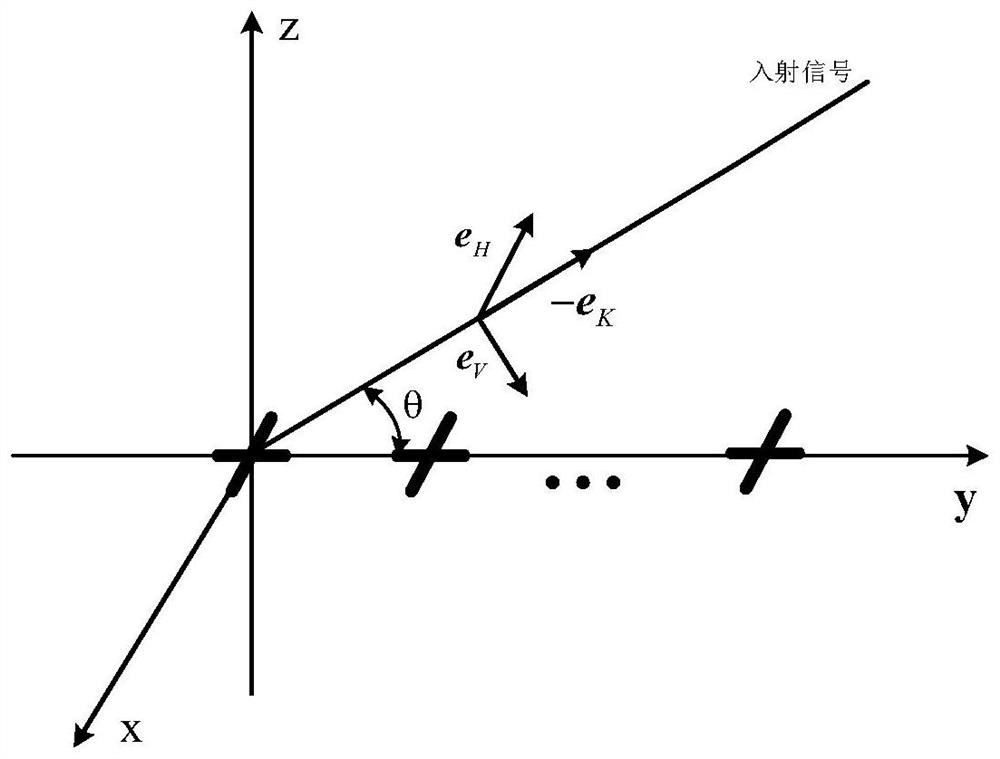
Co-prime array partial polarization signal parameter estimation method based on zero interpolation

A polarization signal and parameter estimation technology, which is applied to the direction of the direction determination device, the direction finder using radio waves, the radio wave direction/bias determination system, etc., which can solve the problem of incomplete array information extraction and insufficient utilization of degrees of freedom. and other problems, to achieve the effect of increasing the number, improving the accuracy of the estimation, and reducing the mutual coupling of the array elements.

Pending Publication Date: 2021-04-30
HANGZHOU DIANZI UNIV
View PDF4 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] Aiming at the deficiencies of the prior art, the present invention proposes a method for estimating the partial polarization signal parameters of a coprime array based on zeroing interpolation, and applies the method to the underdetermined estimation of the partial polarization signal parameters, in addition to estimating the signal wave The direction of arrival and polarization parameters can also be used to make use of all array element information and degrees of freedom corresponding to the virtual array of the coprime array, so as to make up for the defects of incomplete extraction of array information and insufficient utilization of degrees of freedom

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Co-prime array partial polarization signal parameter estimation method based on zero interpolation
  • Co-prime array partial polarization signal parameter estimation method based on zero interpolation
  • Co-prime array partial polarization signal parameter estimation method based on zero interpolation

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0177] Take the extended coprime array, the number of elements of the two sub-arrays is M 1 = 2, M 2 =5, that is, a total of 2M 1 +M 2 -1=8 cross-pole antenna elements for signal reception. Assume that the angles of the 12 incident signals are uniformly distributed between [30, 150], the polarization pointing angles are uniformly distributed between [-π / 3,π / 3], and the polarization ellipticity angles are uniformly distributed in [-π / 5 ,π / 5], the signal polarization is uniformly set to 0.8. The signal-to-noise ratio is set to 20dB, the number of sampling snapshots is 500, the maximum number of iterations is N=100, and the convergence threshold ζ=10 -6 .

[0178] Run the program 10 times to get its spatial power spectrum graph such as Figure 4As shown, the dotted line in the figure represents the real angle of the incident signal. This embodiment can effectively distinguish these 12 signals. Since the number of signals 12 is greater than the number of sensors 8 and the ...

Embodiment 2

[0183] Set the number of subarrays of two extended coprime arrays to M 1 = 2, M 2 =5, a total of 8 physical array elements. Assume that 10 far-field narrowband partially polarized signals equally distributed in [30, 150] are incident on the array. The signal-to-noise ratio is set to 20dB, the number of snapshots is scanned from 50 to 500, and the number of Monte Carlo experiments is 500, and other parameters are the same as in Embodiment 1.

[0184] Figure 5 For using the method of the present invention and the simulation results of the orthogonal subspace method and the quaternion method. It can be seen from the figure that the method of the present invention achieves the minimum root mean square error at each snapshot number. This is because the orthogonal subspace method and the quaternion method only intercept the continuous part of the virtual array, and the noise covariance of the array model is not considered. In particular, the quaternion method has the worst est...

Embodiment 3

[0186] Assuming that 10 far-field narrowband partially polarized signals evenly distributed in [30, 150] are incident on the same array as in Example 1, the signal-to-noise ratio is set to scan from -10dB to 20dB, and the number of Monte Carlo experiments is 500 times. All the other parameters are the same as in Example 1.

[0187] Figure 6 For using the method of the present invention and the simulation results of the orthogonal subspace method and the quaternion method. It can be seen from the figure that the method of the present invention achieves the minimum root mean square error at each signal-to-noise ratio. The quaternion method has the worst estimation effect due to the restriction that the horizontal and vertical signal powers are equal.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a co-prime array partial polarization signal parameter estimation method based on zero interpolation, which is used for estimating a partial polarization signal arrival direction and polarization parameters under an underdetermined condition. The method comprises the following steps of arranging receiving ends according to a co-prime array; constructing a partial polarization signal receiving model and sampling; constructing array element non-repetitive virtual array output and a model noise covariance matrix thereof; initializing an interpolation output signal; initializing an iterative variable; solving a linear equation constraint least square; and estimating the direction of arrival and polarization parameters of the signal. Compared with the prior art, the method is advantaged in that a co-prime array is adopted to replace a nested array during underdetermined estimation of signal parameters, the aperture between array elements is increased, mutual coupling of the array elements is reduced, the signal direction of arrival and polarization parameters can be estimated at the same time, and during processing of co-prime array data, zero interpolation is utilized to interpolate virtual array holes of the co-prime array data; a discontinuous array is changed into a continuous uniform virtual linear array, and the number and precision of estimable signals are improved by using all array element information and degrees of freedom.

Description

technical field [0001] The invention belongs to the technical field of array signal processing, and in particular relates to the parameter estimation of partially polarized incident signals in applications such as radar and communication. method for estimating the parameters. Background technique [0002] Array direction finding technology uses sensors to measure the incoming wave direction of incident signal sources, and is widely used in radar, communication and other technical fields. In the past few decades, researchers have done a lot of research around fully polarized signals and uniform linear arrays. However, the signals in practical applications are often not completely polarized, and the polarization directions are also different, and the uniform line array can only perform direction finding for signals whose number is smaller than the number of array elements. When the signal is partly polarized and the number of signal sources is greater than the number of arra...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01S3/14
CPCG01S3/146
Inventor 潘玉剑高晓欣
Owner HANGZHOU DIANZI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com