Check patentability & draft patents in minutes with Patsnap Eureka AI!

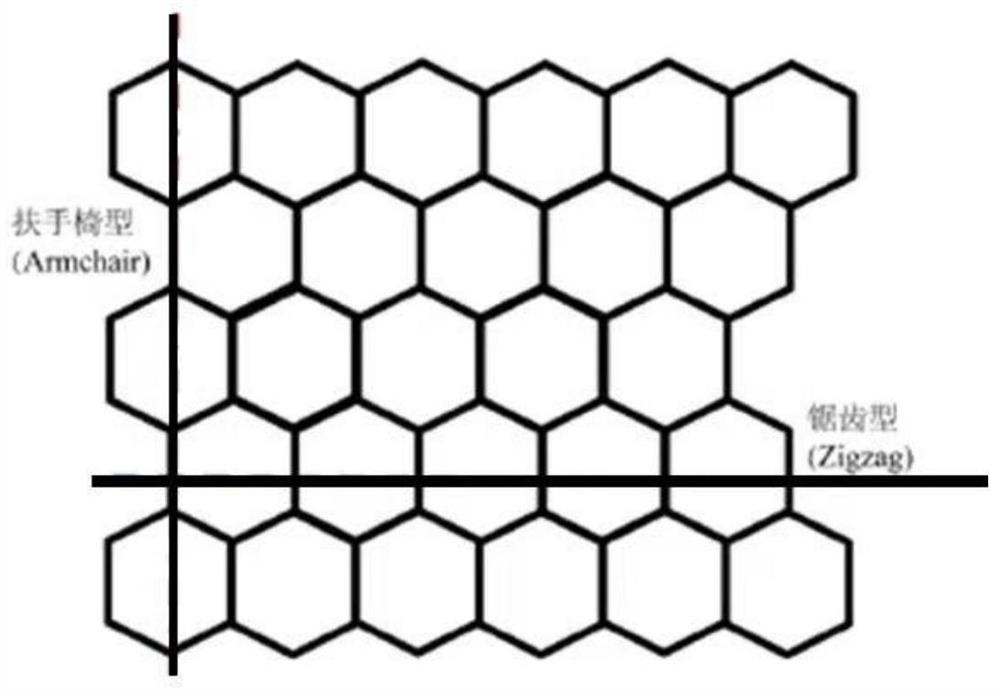
Method for solving critical strain of graphene

A critical strain, graphene technology, applied in the field of graphene critical strain solution, can solve problems such as a large number of computing resources

Pending Publication Date: 2021-08-17
CHONGQING UNIV OF POSTS & TELECOMM
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The existing method for calculating the critical strain of graphene is a molecular dynamics simulation calculation method, but this method requires a large amount of computing resources

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for solving critical strain of graphene
  • Method for solving critical strain of graphene
  • Method for solving critical strain of graphene

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0021] In this embodiment, what is introduced is the potential function Tersoff-Brenner potential function that we adopt, and this potential function is widely used in the calculation of the interatomic potential of graphene and single-walled carbon nanotubes:

[0022] V ij =V R (r ij )-B ij V A (r ij ) (1)

[0023] In the formula, subscript i, j represent atom, r ij Indicates the distance between two atoms, B ij Represents the key number item; V R Represents the repulsive force term between atoms, V A Indicates the attractive force term for interactions between atoms. They can be calculated by the following formula:

[0024]

[0025]

[0026] f ij (r) is a smooth cut-off function that limits the potential energy, determined by Equation 4:

[0027]

[0028] Among them, the healthy sequence function B ij Indicates the influence of atom k on the bond energy between atoms i and j under consideration of the many-body interaction:

[0029] B ij =(b ij +b j...

Embodiment 2

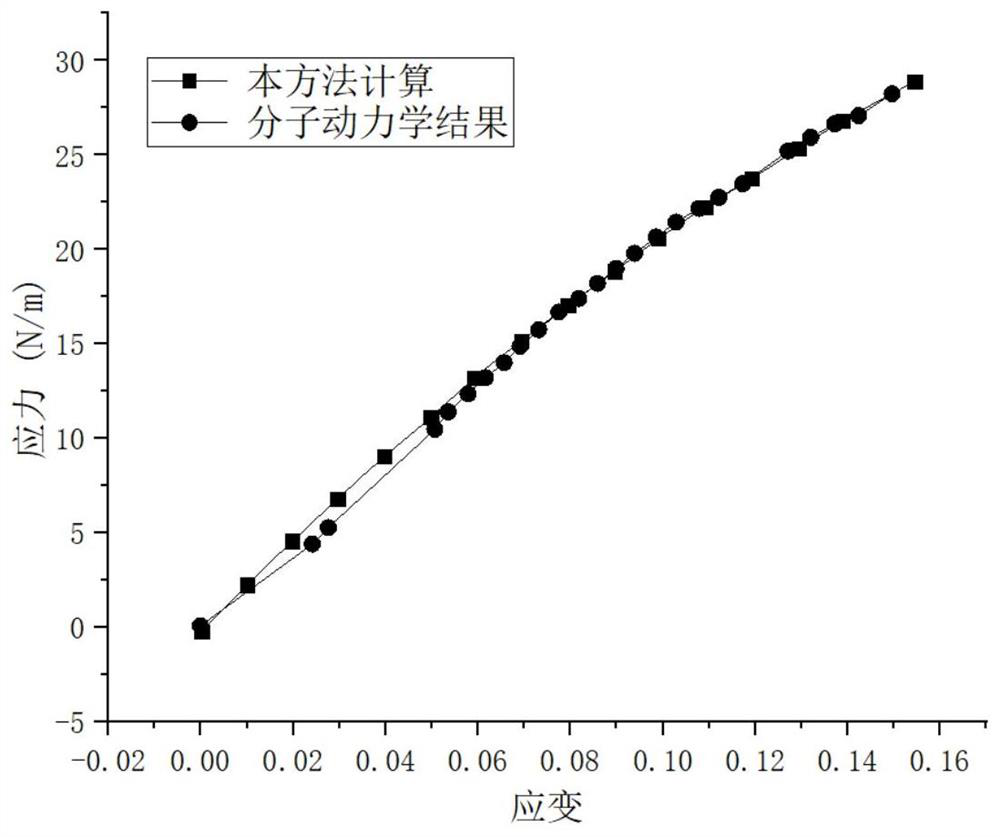
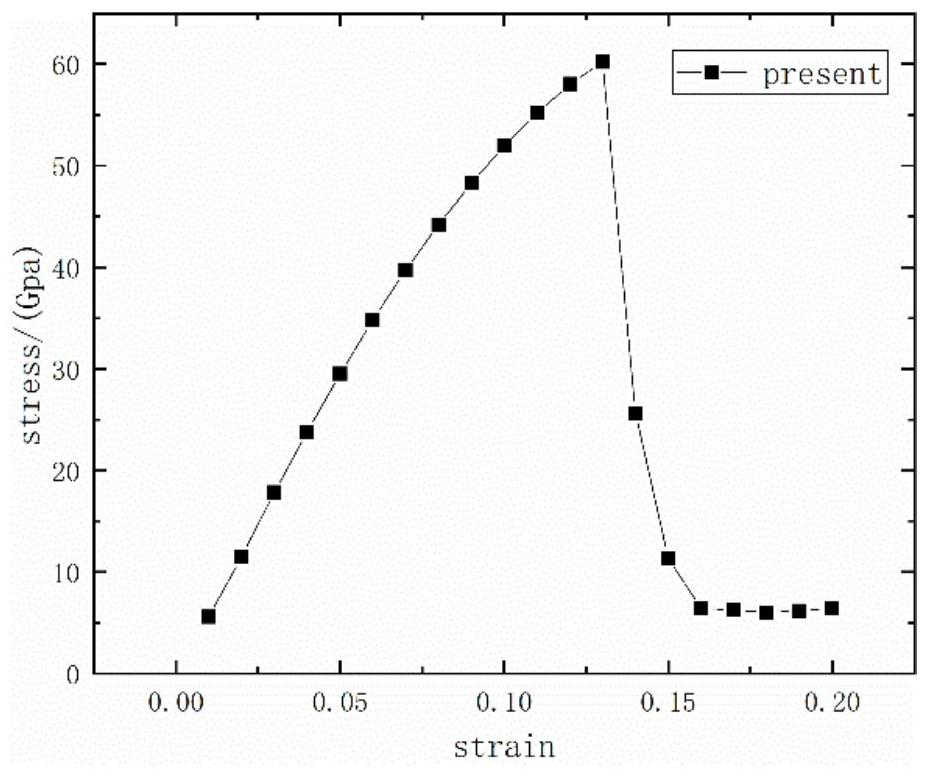
[0070] Please refer to Figure 1 to Figure 5 , Figure 1 to Figure 5 The relationship of this method to the mechanical properties of graphene with the strain after loading is provided.

[0071] in, Figure 4 The embodiment of the present invention provides a schematic diagram of the relationship between Poisson's ratio and strain of graphene stretched along the Armchair direction, in Figure 4 It can be seen that the graphene has broken when the slope k=0.

[0072] in, Figure 5 Provide the schematic diagram of the graphene biaxial tension failure boundary for the example of the present invention, in Figure 5 The closed area enclosed by the middle graph and the two axes of x-axis and y-axis is the effective area of ​​graphene. When this area is exceeded, graphene will break.

[0073] The purpose of the present invention is to provide a new method for calculating the critical strain of graphene under load, which can calculate the critical strain and mechanical properties ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A graphene critical strain solving method applies a load in an Armchair direction or a Zigzag direction to graphene, and comprises the following steps: S1, determining a constitutive relation when the graphene is subjected to the load according to a lowest energy principle; and S2, judging the critical strain of the graphene according to abnormal changes of mechanical property parameters such as Young modulus and Poisson's ratio. According to the method, on the basis of the Cauchy-Born criterion, the strain energy, the Young modulus and the Poisson ratio of graphene are determined through a continuum mechanics method. A constitutive relation is determined when the graphene is loaded according to a lowest energy principle, and a specific structure of the graphene subjected to the load is determined. Through the method, the critical strain of the graphene under the plane load can be calculated more conveniently, and the method can be further expanded to the solution of the loaded critical strain of a novel two-dimensional material.

Description

technical field [0001] The invention relates to the field of two-dimensional nanomaterials, in particular to a new method for solving the critical strain of graphene. Background technique [0002] In 2004, humans obtained graphene for the first time using micromechanical exfoliation. Due to its excellent mechanical, thermal, electrical, magnetic and acoustic properties, it is expected to be widely used in high-performance nanoelectronic devices, composite materials, field emission materials, gas sensors, energy storage, etc. Potential new materials. With the successive discoveries of silicene and germanene, two-dimensional materials represented by graphene have become the new stars that scientists are most concerned about in industries such as looking for future electronics and composite materials. Therefore, a comprehensive grasp and in-depth understanding of the mechanical properties play an irreplaceable role in the development and application of the entire graphene-lik...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G16C10/00G16C60/00
CPCG16C10/00G16C60/00
Inventor 禄盛刘宝峰陈翔马莹邓聪颖朴昌浩
Owner CHONGQING UNIV OF POSTS & TELECOMM
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com