Practical unexposed public key encrypting system

A public key encryption and non-extensible technology, which is applied to the public key and key distribution of secure communication, can solve the problems of unproven security, insecurity, impracticality, etc.

Inactive Publication Date: 2007-03-07
胡玉莲
View PDF0 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

And it has been proven that there are cryptographic schemes that are secure under the random oracle model, but not secure in the real world, regardless of the choice of hash function
[0014] Meanwhile, there exist identity-based public-key cryptosystems that are secure under standard assumptions, but none of them are practical
Some practical identity-based cryptographic schemes have also been proposed, but they have not been proven secure under the standard hard problem assumption

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Practical unexposed public key encrypting system
  • Practical unexposed public key encrypting system

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

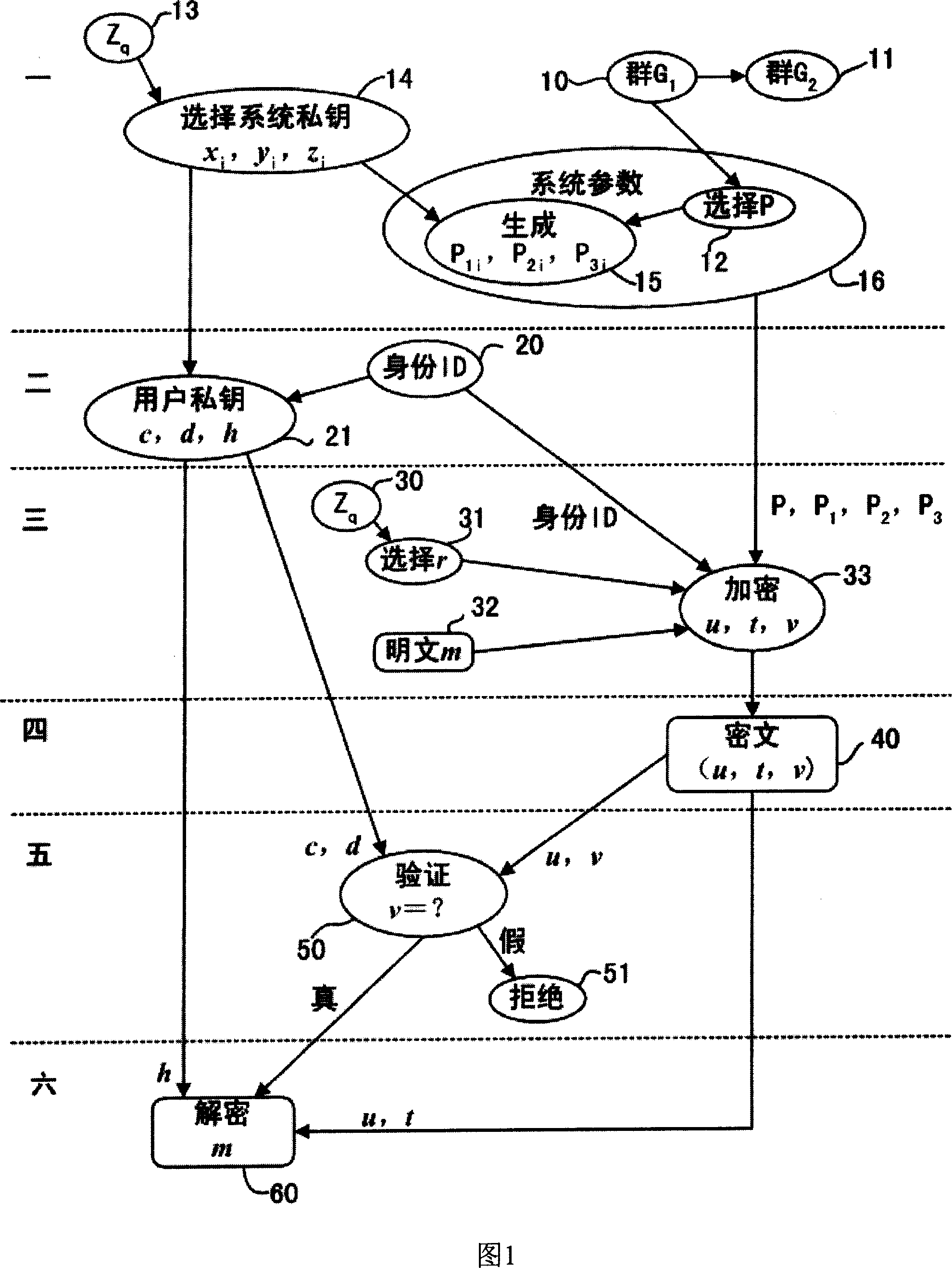
[0200] When there is only one trusted center, the proposed identity-based public key cryptosystem is used for secure communication, assuming that user B sends information m to user A. Then B first encrypts m with A's public key, and sends the encrypted ciphertext to A. After A obtains the ciphertext, he recovers m with his own private key. Specific steps are as follows:

[0201] The first part trusted center establishes system parameters:

[0202] (a) Generate the first cyclic group G 1 and the second cyclic group G 2 , where G 1 is an additive group of points on a supersingular elliptic curve or Abelian variety, G 2 is a multiplicative group of finite fields;

[0203] (b) Pick a feasible pairing e: G 1 ×G 1 →G 2 , which can be formed by the first cyclic group G 1 The two elements of generate the second cyclic group G 2 an element of

[0204] (c) Randomly choose a generator P∈G 1 ;

[0205] (d) randomly select x, y, z∈Z q , calculate P 1 =xP,P 2 =yP,P 3 = zP;...

specific Embodiment approach 2

[0230] When there are n trusted centers, where n≥2, and the proposed identity-based public key cryptosystem is used for secure communication, it is assumed that user B sends information m to user A. Then B first encrypts m with A's public key, and sends the encrypted ciphertext to A. After A obtains the ciphertext, he recovers m with his own private key. Specific steps are as follows:

[0231] The first part n trusted centers establish system parameters:

[0232] (a) Generate the first cyclic group G 1 and the second cyclic group G 2 , where G 1 is an additive group of points on a supersingular elliptic curve or Abelian variety, G 2 is a multiplicative group of finite fields;

[0233] (b) Pick a feasible pairing e: G 1 ×G 1 →G 2 , which can be formed by the first cyclic group G 1 The two elements of generate the second cyclic group G 2 an element of

[0234] (c) Randomly choose a generator P∈G 1 ;

[0235] (d) Randomly pick x i ,y i ,z i ∈ Z q , calculate P ...

specific Embodiment approach 3

[0268] When the proposed general public key cryptosystem is used for secure communication, it is assumed that user A sends information m to user B. A encrypts m with B's public key, and sends the encrypted ciphertext to B. After B obtains the ciphertext, he recovers m with his own private key. Specific steps are as follows:

[0269] The first part generates a key pair:

[0270] Establish a cyclic group G of order q with a large prime number.

[0271] User B chooses a primitive g in the cipher group G, and in Z q Randomly select the first index x, the second index y and the third index z, and reserve (x, y, z) as the private key; use the following formula to calculate the first group element c, the second group element element d, the third group element h:

[0272] c=g x ,

[0273] d=g y ,

[0274] h=g z ,

[0275] Use (g, c, d, h) as the public key and make it public;

[0276] The second part is encrypted:

[0277] User A obtains user B's public key (g, c, d, h) f...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

This invention relates to public key codes system against lunch time attack and adaptive selection message attack without leaking any private keys or message information. In the invention message is converted into coded message with accurate keys for decoding, if message is legal, then decoding message and if message is not legal then denying; if legal message is non artificial based on standard hypoesthesia to compute Diffie-Hellman problem or double Diffie-Hellman difficulty and Hush function non collision.

Description

technical field [0001] The present invention relates to privacy or information security. In particular, it relates to a secure communication system and method for improving the security of a data processing system. The proposed public key cryptosystem is secure against both lunchtime attack and adaptive chosen ciphertext attack. Background technique [0002] Confidentiality and security are important elements of today's networked society. The information transmitted is limited to the intended recipients and may not be suitable for everyone. To secure communications, encryption methods are useful. A cryptographic system means that the sender processes the sent information in a certain way and sends it to the receiver. This information is still safe, that is, only the designated receiver can recover the information. A cryptographic system converts information, known as plaintext, into an encrypted form known as ciphertext. Encryption is the clever processing and transform...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/30H04L9/08
Inventor 胡玉莲
Owner 胡玉莲
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap