Multi-focus image fusion method based on compressive sensing

A multi-focus image, compressed sensing technology, applied in the field of image processing, can solve the problems of high computational complexity, noise and stripes in fusion results, and achieve the effect of good visual effect, small amount of data, and saving storage space.

Active Publication Date: 2012-03-28
XIDIAN UNIV
View PDF3 Cites 37 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, there are few studies on applying compressive sensing theory to image fusion.
Scholar T.Wan and others took the lead in applying the theory of compressed sensing to image fusion, see the article "Compressive Image Fusi

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Multi-focus image fusion method based on compressive sensing
  • Multi-focus image fusion method based on compressive sensing
  • Multi-focus image fusion method based on compressive sensing

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0029] Reference figure 1 The specific implementation steps of the present invention are as follows:

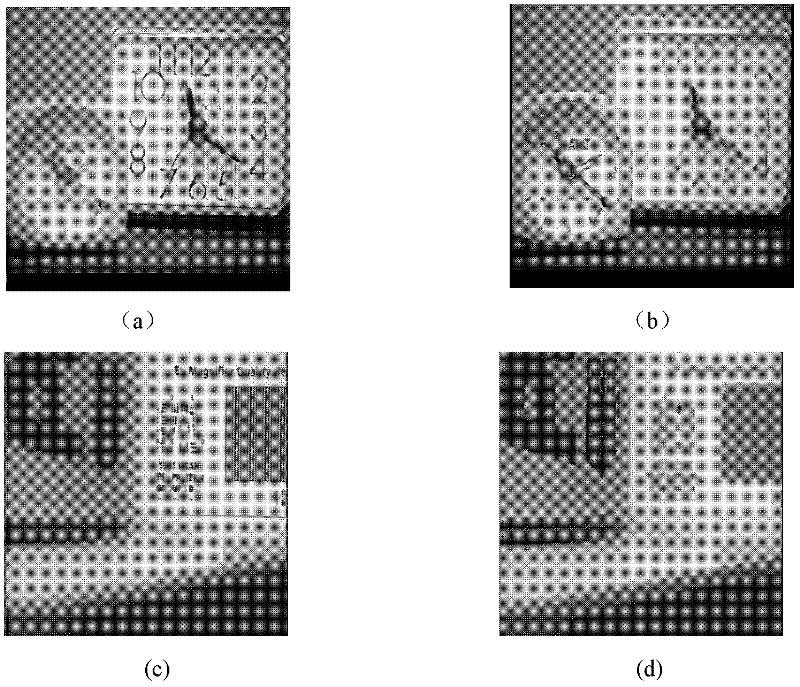
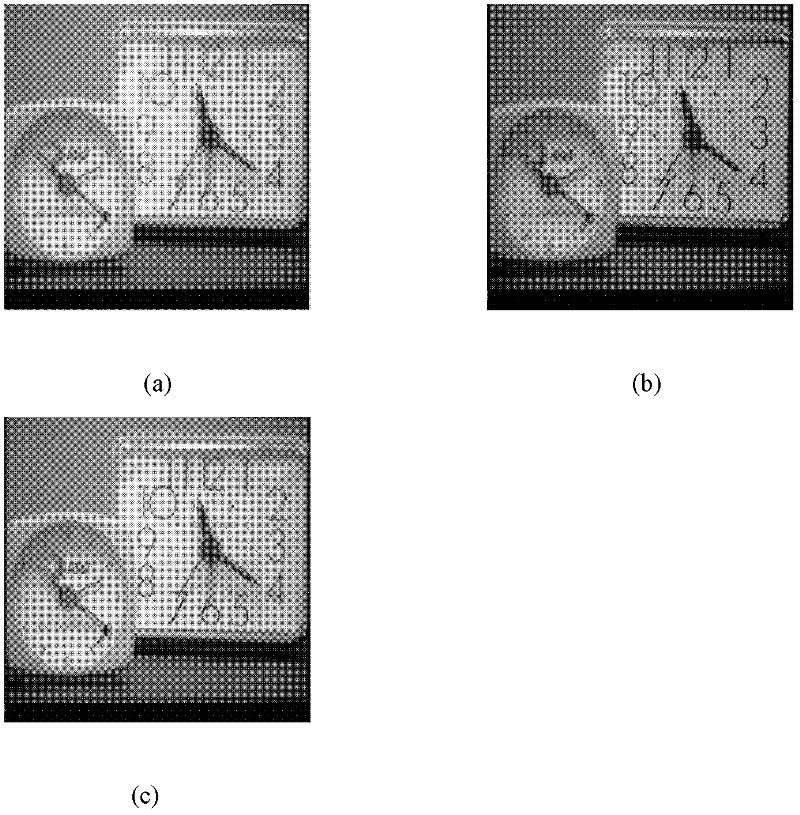
[0030] Step 1. Divide the input two multi-focus images A and B into blocks and calculate the average gradient of each image sub-block with

[0031] Images A and B are two left-focused and right-focused images, respectively. The clear parts of the two images have complementary information, and the purpose is to obtain an all-focused image with clear left and right sides through fusion. The image is divided into blocks, which is beneficial to processing and can reduce the computational complexity. The present invention divides the two multi-focus images A and B into image sub-blocks with a size of 32×32, and calculates the average gradient of each image sub-block , Calculated according to the following formula:

[0032] ▿ G ‾ I = 1 M X N X i = 1 M X j = 1 N [ Δxf ( i , j ) 2 + Δyf ( i , j ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a multi-focus image fusion method based on compressive sensing and relates to the technical field of image processing. By the multi-focus image fusion method, the main problem that a clear image with all focused sceneries is difficult to acquire due to a limited depth of field of an optical lens in the prior art can be solved. The multi-focus image fusion method is implemented by the following steps of: (1) blocking an image; (2) calculating an average gradient of each image sub block to determine a fusion weight value; (3) performing sparse representation on each image sub block and observing each image sub block by adopting a random Gaussian matrix; (4) performing weighted fusion on the fusion weight value of an observed value of each image sub block; and (5) recovering a fused image observed value by adopting an orthogonal matching traceback algorithm and performing wavelet inverse transformation on a recovered result to acquire a fused fully-focused image. By the multi-focus image fusion method based on the compressive sensing, a better image fusion effect can be achieved and higher convergence property is realized; and the method can be applied to fusion of a multi-focus image.

Description

technical field [0001] The invention belongs to the technical field of image processing and relates to image fusion technology, in particular to a multi-focus image fusion method combined with compressed sensing theory, which can be used in multi-focus image fusion. Background technique [0002] As an emerging scientific research field, image fusion has broad prospects for development. It obtains a more accurate, comprehensive and reliable image description of the same scene or target by extracting and integrating information from multiple sensor images, so as to further analyze and understand the image and detect, identify or track the target. From the early 1980s to the present, multi-sensor image fusion has aroused widespread interest and research boom worldwide, and it has great potential in the fields of automatic target recognition, computer vision, remote sensing, machine learning, medical image processing, and military applications. Wide application prospects. Afte...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06T5/50
Inventor 王爽焦李成杨奕堂刘芳杨淑媛侯彪钟桦刘忠伟杨国辉
Owner XIDIAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap