A space-based observation simulation system and method targeted at satellite targets and fixed star targets
A target and satellite technology, applied in the field of space-based observation and simulation systems, can solve the problems of less research and simulation, and achieve the effect of improving fidelity
Inactive Publication Date: 2016-04-06
ACAD OF OPTO ELECTRONICS CHINESE ACAD OF SCI
View PDF5 Cites 16 Cited by
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
[0006] At present, the research on space-based observations is often the study and simulation of satellite observation platforms and observation loads alone, and there are relatively few studies and simulations on various objects including the entire space-based observation process
Method used
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View moreImage
Smart Image Click on the blue labels to locate them in the text.
Smart ImageViewing Examples
Examples
Experimental program
Comparison scheme
Effect test
Embodiment Construction
[0045] The specific implementation manner of the present invention will be described below in conjunction with the technical scheme and the accompanying drawings.
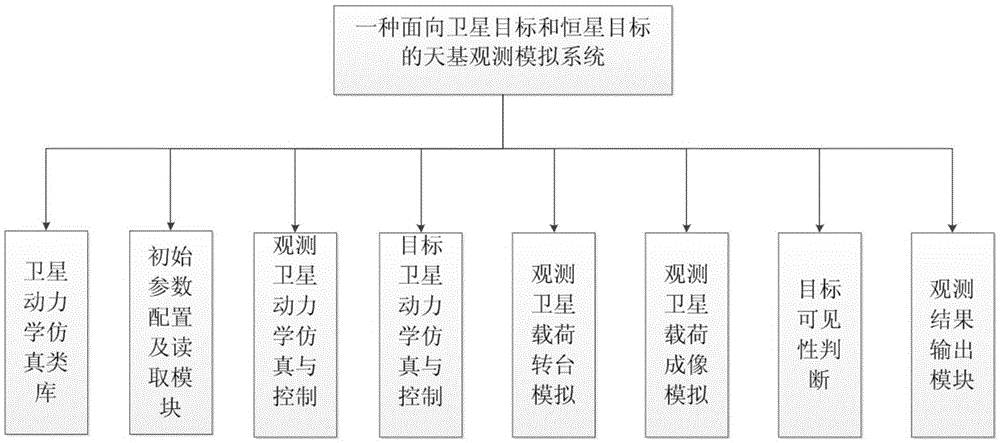
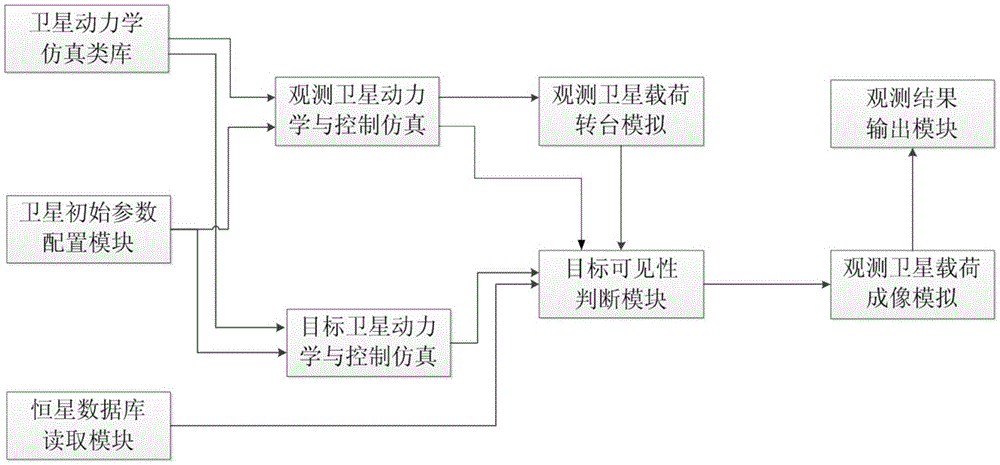
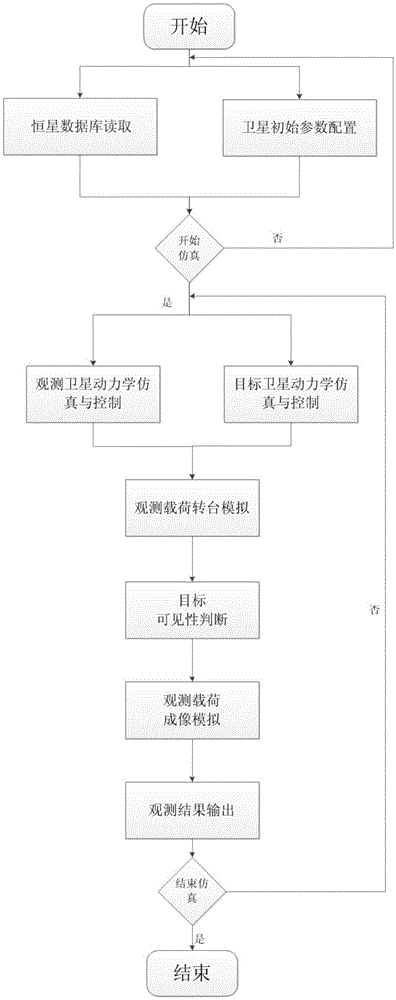
[0046] Such as figure 1 , 2 As shown, the present invention provides a space-based observation simulation system for satellite targets and stellar targets. It mainly includes star database reading module, satellite dynamics simulation class library, satellite initial parameter configuration module, observation satellite dynamics simulation and control, target satellite dynamics simulation and control, observation satellite load turntable simulation module, target visibility judgment module, Observation satellite load imaging simulation, observation result simulation output module, the data communication between modules is mainly realized through the form of internal interface, the operation process of the whole system is as follows: image 3 shown.
[0047] The data transformation between different coordinate sy...
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More PUM
Login to View More Abstract
The invention relates to a space-based observation simulation system and method targeted at satellite targets and fixed star targets, and realizes simulated observation performed by observation satellites on the satellite targets and fixed star targets. The system comprises a fixed star database reading module, a satellite dynamics simulation database, a satellite initial parameter configuration module, observation satellite dynamics simulation and control, target satellite dynamics simulation and control, observation satellite load rotary table simulation, a target visibility determination module, observation satellite load imaging simulation and an observation result simulation output module. According to the invention, with whole space-based observation physical process simulation as a starting point, a space-based observation process including various models of the observation satellites, observation load, the target satellites, the fixed star, etc. is established and simulated, and space-based observation simulation results with high confidence are output.
Description
technical field [0001] The present invention relates to computer simulation techniques for space-based observations. To be precise, it is a space-based observation simulation system and method for satellite targets and stellar targets. Background technique [0002] In order to use space more effectively and explore space more deeply, all space powers are actively researching space surveillance technology. Space surveillance is mainly to detect, identify and track specific space targets, mainly through ground-based observation systems and space-based observation systems. Compared with the ground-based observation system, the space-based observation system has the following significant advantages: it is not restricted by geographical location and meteorological conditions, and can observe targets from different azimuths; Higher signal-to-noise ratio; the space-based observation system is in orbit, and only one star is needed to cover the entire geosynchronous orbit. In view...
Claims
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More Application Information
Patent Timeline
Login to View More IPC IPC(8): G01D18/00G01C25/00
CPCG01C25/00G01D18/00
Inventor 张扬欧阳高翔甘庆波项磊
Owner ACAD OF OPTO ELECTRONICS CHINESE ACAD OF SCI