Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Target tracking new algorithm based on fractional fuzzy function under stably distributed noise

A fractional fuzzy, stable distribution technology, applied in the direction of radio wave reflection/re-radiation, using re-radiation, measurement devices, etc., can solve problems such as performance degradation

Inactive Publication Date: 2016-10-26
DALIAN UNIV
View PDF0 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

There is no finite second-order moment in the stable distributed noise, therefore, the traditional estimation methods based on second-order statistics will inevitably suffer performance degradation in the impulsive noise environment

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Target tracking new algorithm based on fractional fuzzy function under stably distributed noise
  • Target tracking new algorithm based on fractional fuzzy function under stably distributed noise
  • Target tracking new algorithm based on fractional fuzzy function under stably distributed noise

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

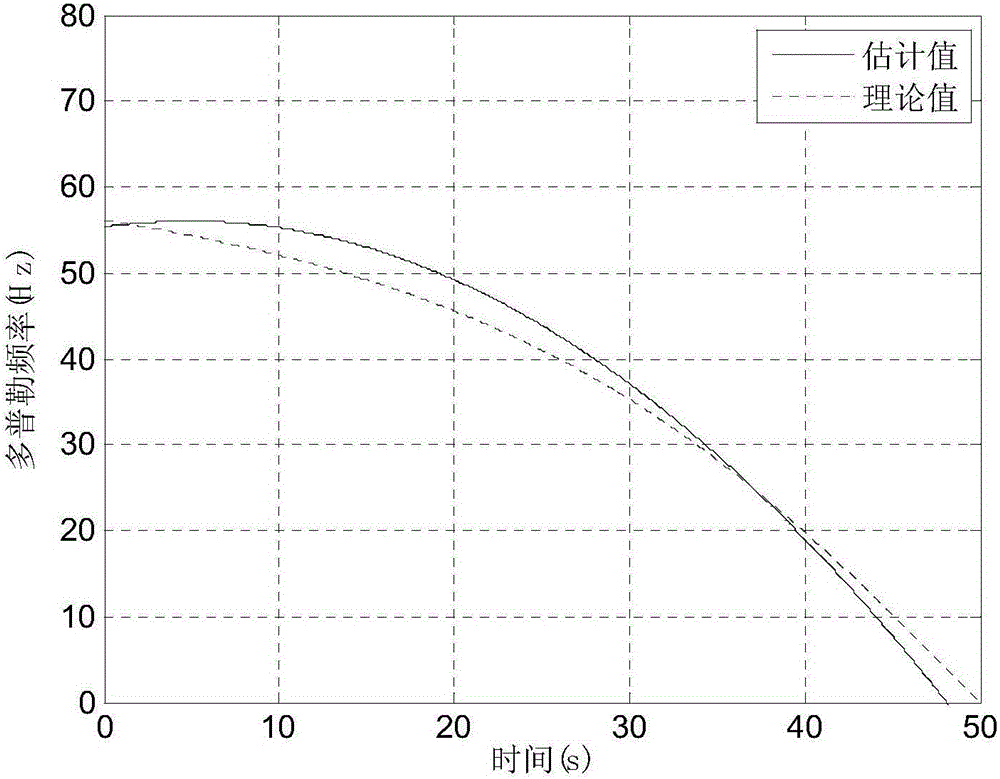
[0142] Embodiment 1: The characteristic index of the noise is set to α=1.4, and the generalized signal-to-noise ratio GSNR=12dB. figure 2 The estimated performance of the Doppler frequency is shown and compared to theoretical values. It can be seen from the figure that the algorithm in this paper not only effectively suppresses the interference of impulse noise, but also has better estimation performance.

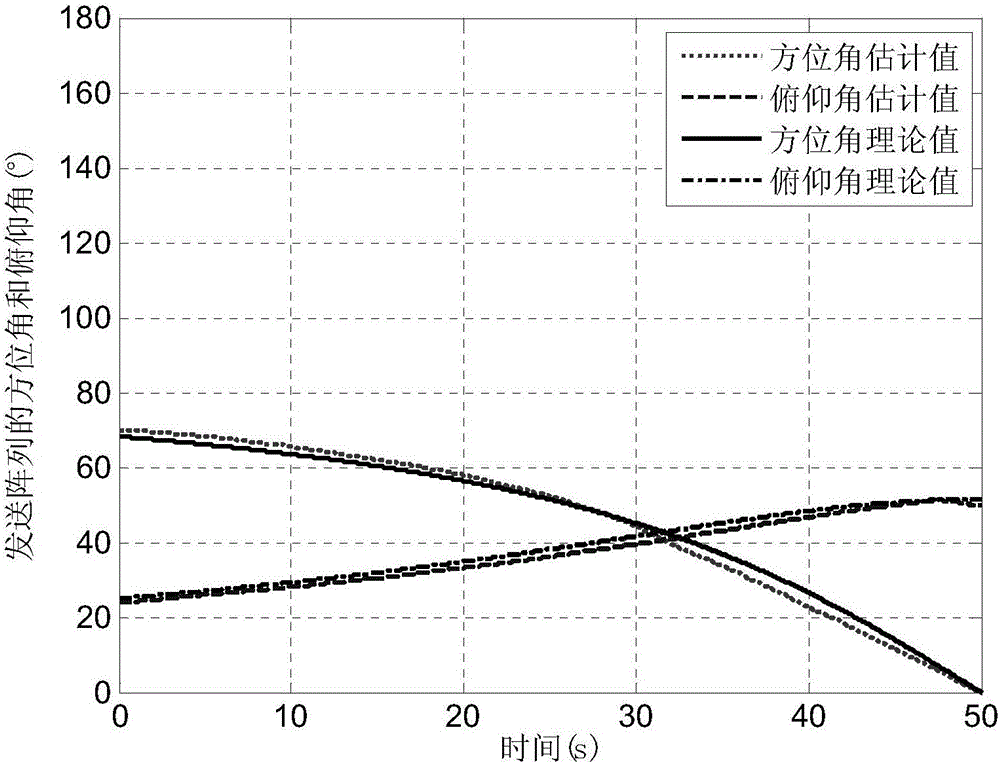
[0143] Figure 3 shows the dynamic estimation results of the azimuth and elevation angles of the transceiver array at different times. It can be seen from the figure that the algorithm in this section has better estimation performance. It can be seen that the algorithm in this paper not only has a good ability to suppress impulse noise interference, but also has a good estimation accuracy, which lays the foundation for the subsequent location of interference sources.

Embodiment 2

[0144] Embodiment 2: In this experiment, the generalized signal-to-noise ratio is set as GSNR=12dB. Given a new definition, Indicates the root mean square error of each parameter estimate at different characteristic indices. Fig. 4 shows the RMSE of target parameter estimation as a function of noise characteristic index. It can be seen from the figure that the algorithm in this paper has good estimation performance.

Embodiment 3

[0145] Embodiment 3: In this experiment, the characteristic index of noise is α=1.4. Under different SNR environments, the RMSE calculation formula for target parameter estimation refers to the definition formula RMSE2 in Experiment 2. Figure 5 shows the RMSE of target parameters and localization estimates as a function of generalized SNR.

[0146] It can be seen from Fig. 5(a) that this algorithm has better performance in azimuth and elevation angle estimation, and the RMSE of parameter estimation becomes smaller as the generalized signal-to-noise ratio increases. Figure 5(b) shows the RMSE of Doppler frequency estimation. It can be seen from the figure that the RMSE limit of Doppler frequency estimation is relatively flat, because: the estimation of Doppler frequency in the algorithm in this section is through Estimating the Doppler frequency parameters is realized, and the estimation of the Doppler frequency parameters is realized by searching the peak of FLOS-FAF. Based o...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a target tracking new algorithm based on a fractional fuzzy function under stably distributed noise, belonging to the technical field of computer application. At first, a new signal model is proposed, and in the fractional order Fourier transform domain, the instantaneous estimation of doppler frequency is realized by the peak point searching of FLOS_FAF. And then a projection approximation subspace angle tracking algorithm of the fractional order fuzzy function based on fraction low order statistics is proposed, and the real-time estimation formula of azimuth and pitch angle in the impulsive noise environment can be realized.

Description

technical field [0001] The invention relates to a new target tracking algorithm of an improved fractional fuzzy function under stable distribution noise, and belongs to the technical field of computer applications. Background technique [0002] Modern civil aviation plays an important role in the overall development of the national economy and has become a powerful force to promote economic prosperity and social progress. With the increase of the total number of radio stations (stations) in our country, the probability of civil aviation radio frequency interference also increases, and ensuring the safe use of civil aviation radio frequency is one of the keys to civil aviation flight safety. [0003] Due to the high flying altitude of civil aviation aircraft, its communication signal coverage can reach hundreds of thousands of square kilometers. This means that interference sources in this range may have an impact on flight safety. In particular, the time and location of ma...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01S13/68
CPCG01S13/68
Inventor 李丽
Owner DALIAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com