Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Regular Hartley transform chaotic dual random phase coding optical image encryption method

A technology of chaotic random phase and double random phase, which is applied in the direction of secure communication through chaotic signals, image data processing, image data processing, etc., can solve the inconvenience of key management and transmission, the encryption system is vulnerable to chosen plaintext attack and known plaintext Attacks, random phase masks are inconvenient to update, etc., to achieve the effect of convenient key management and transmission, resistance to known plaintext attacks, and resistance to chosen plaintext attacks

Inactive Publication Date: 2017-03-29
TIANJIN UNIV
View PDF2 Cites 8 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] 1) The key is a random phase mask of the image size, therefore, key management and transmission are inconvenient (see literature [6]);
[0006] 2) Since the random phase mask is inconvenient to update, the encryption system is vulnerable to chosen plaintext attack and known plaintext attack (see literature [7] and [8])

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Regular Hartley transform chaotic dual random phase coding optical image encryption method
  • Regular Hartley transform chaotic dual random phase coding optical image encryption method
  • Regular Hartley transform chaotic dual random phase coding optical image encryption method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

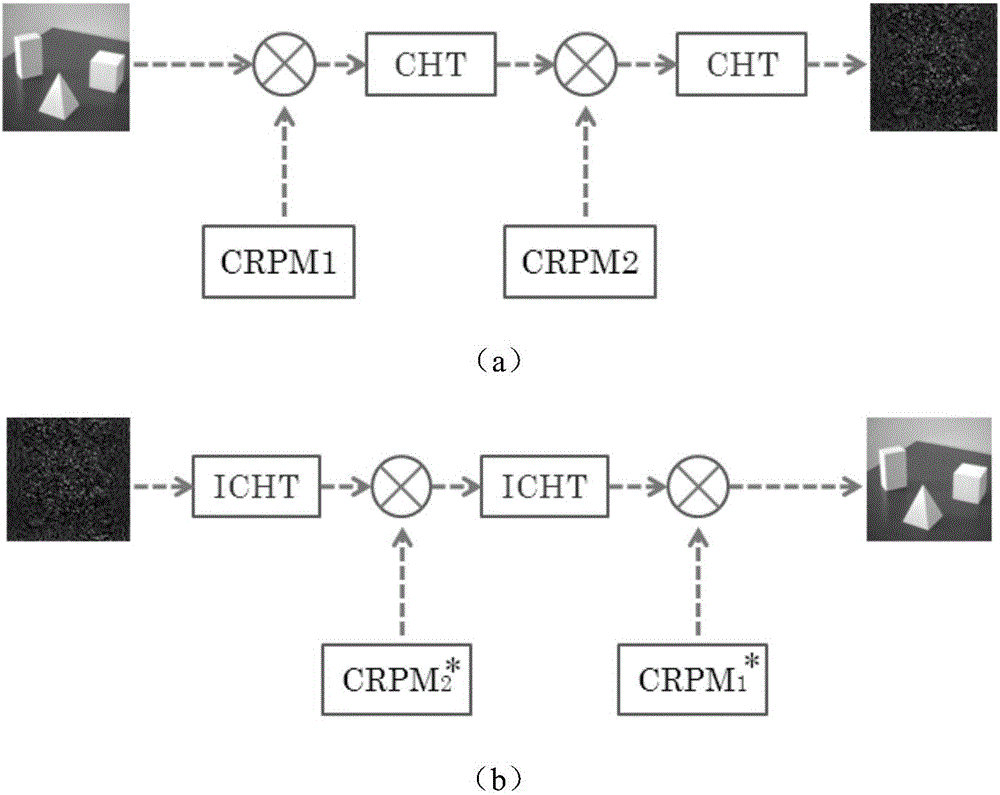
[0073] An optical image encryption method based on regular Hartley transform and chaotic double-random phase encoding, the schematic diagram of the encryption and decryption process is as follows figure 1 As shown, the encryption method consists of the construction of the two-dimensional regular Hartley transform system, the generation of the chaotic key, and the process of image encryption and decryption.

[0074] (1) Construction of two-dimensional regular Hartley transform system:

[0075] In the encryption method provided by the present invention, through rigorous mathematical derivation and proof, it is found that the two-dimensional canonical Hartley transform can be composed of a linear combination of two two-dimensional linear canonical transformations (LCT). Just as the linear canonical transform (LCT) is a more generalized Fourier transform and fractional Fourier transform, the canonical Hartley transform is a more generalized Hartley transform and fractional Hartley...

Embodiment 2

[0082] Combine below figure 1 1. The design principle introduces the scheme in embodiment 1 in detail, see the following description for details:

[0083] An optical image encryption method based on regular Hartley transform and chaotic double-random phase encoding, the schematic diagram of the encryption and decryption process is as followsfigure 1 shown. The encryption method consists of the construction of two-dimensional regular Hartley transform system, the generation of chaotic key, and the process of image encryption and decryption. The specific implementation manners of these three parts will be described in detail below.

[0084] (1) Construction of two-dimensional regular Hartley transform system:

[0085] After rigorous mathematical derivation and proof (the proof and derivation process is omitted here), it is found that the two-dimensional canonical Hartley transform (CHT) can be composed of a linear combination of two two-dimensional linear canonical transformat...

Embodiment 3

[0105] Below in conjunction with specific accompanying drawing, the scheme in embodiment 1 and 2 is carried out feasibility verification, see the following description for details:

[0106] Adopt the encryption method provided by the implementation of the present invention to an image (such as figure 2 As shown in (a), after encryption, the obtained encrypted image is as follows figure 2 (b) shown.

[0107] Depend on figure 2 (b) It can be seen that any information of the original image is hidden. When all the keys are correct, the decrypted image is as follows figure 2 (c) shown. Depend on figure 2 (c) It can be seen that the original image can be completely restored. It shows that the encryption and decryption of grayscale images using this system is successful.

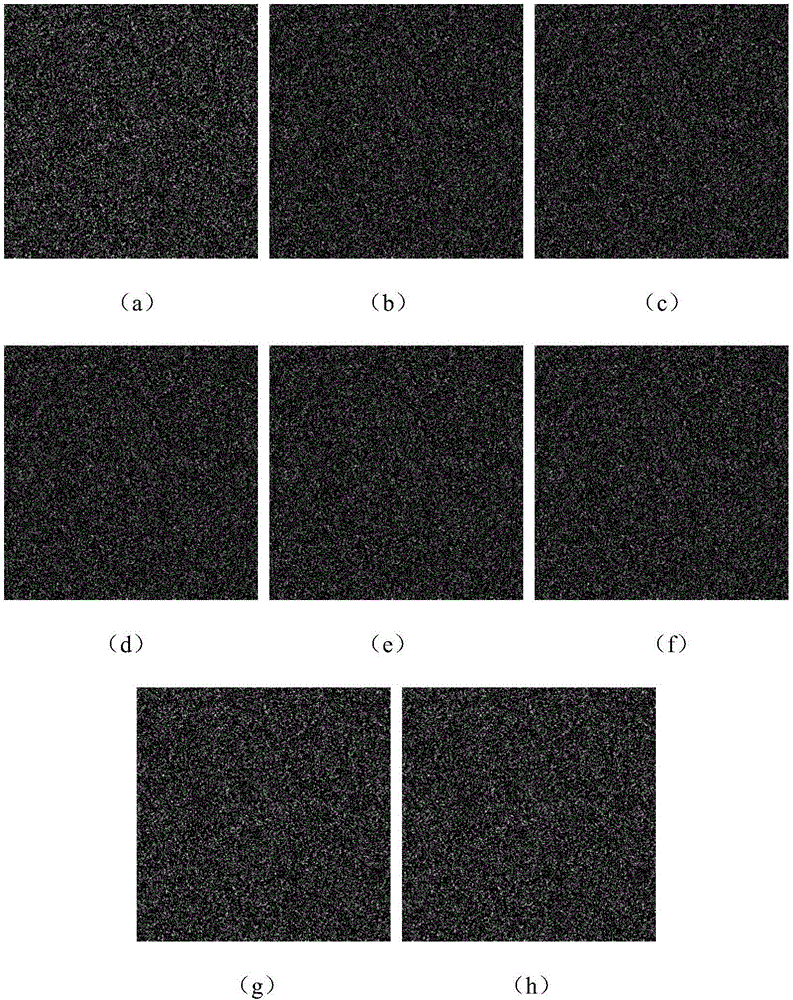
[0108] In addition, when one key is wrong and other keys are correct, the decryption result is as follows: image 3 (a)-3(h). It can be seen that the security of the system can be guaranteed.

[0109...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention relates to the technical field of image information security and optical information processing, and aims to provide an optical image encryption / decryption method, which can effectively resist known plain attack and select plain attack, makes key management and transmission more convenient, further ensures security, and has excellent capabilities of resisting a violence attack, a statistical attack, a noise attack and a cut attack. The technical scheme adopted by the present invention is a regular Hartley transform chaotic dual random phase coding optical image encryption method. The method comprises the following steps: 1) constructing a two-dimensional regular Hartley transform system; 2) generating a chaotic key, wherein two random phase masks that function as a master key are separately generated by a one-dimensional ICMIC chaotic system controlled by different chaotic parameters, an initial value and a control parameter of the ICMIC chaotic system are used as the master key; and 3) encrypting and decrypting an image. The method provided by the present invention is mainly applied to the field of image information security and optical information processing.

Description

technical field [0001] The invention relates to the technical fields of image information security and optical information processing, in particular to an optical image encryption method based on regular Hartley transformation and chaotic double random phase encoding. Background technique [0002] As one of the most popular multimedia forms at present, digital images are widely used in the fields of politics, economy, military affairs, education and so on. In today's highly developed Internet technology, how to protect digital images from tampering, illegal copying and dissemination has important practical significance. The research on image encryption technology has become one of the hotspots in the field of information security. [0003] Optical information processing technology has aroused great interest in the field of image encryption research because of its high processing speed, high parallelism, and fast realization of convolution and correlation operations (see lit...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F21/10G06F21/62G06T1/00H04L9/00
CPCG06F21/10G06F21/62G06T1/0021H04L9/001
Inventor 唐晨苏永钢李碧原谷帆程佳佳
Owner TIANJIN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com