Check patentability & draft patents in minutes with Patsnap Eureka AI!

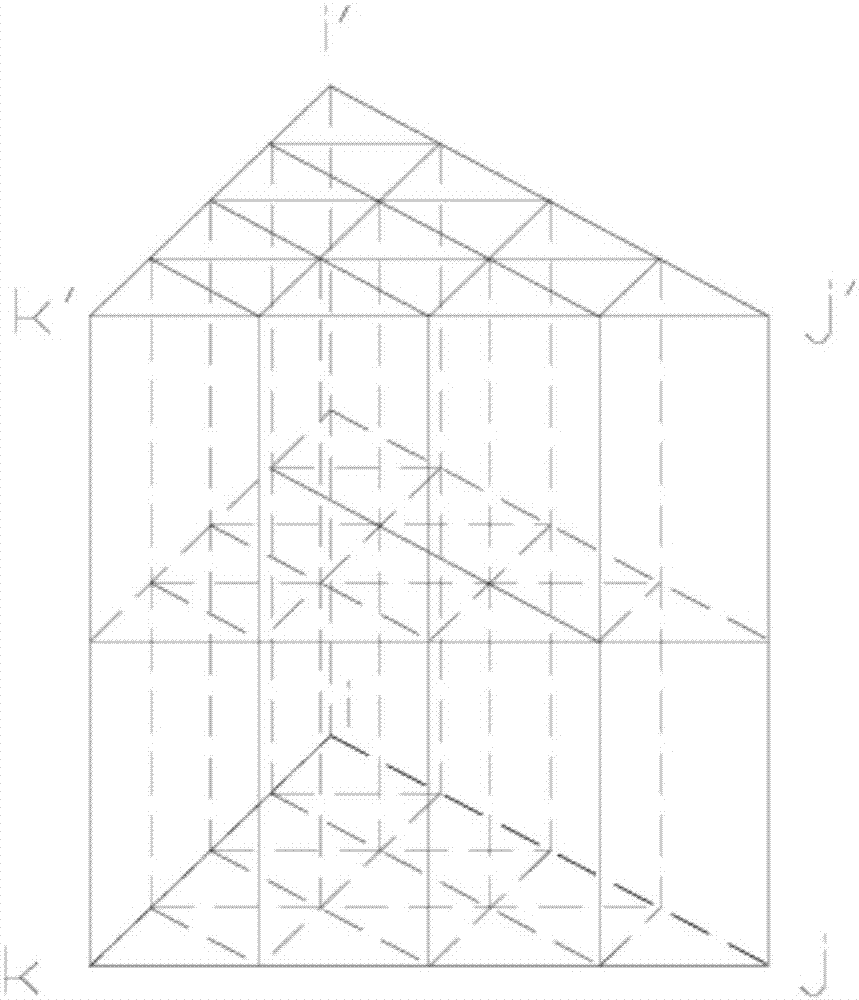
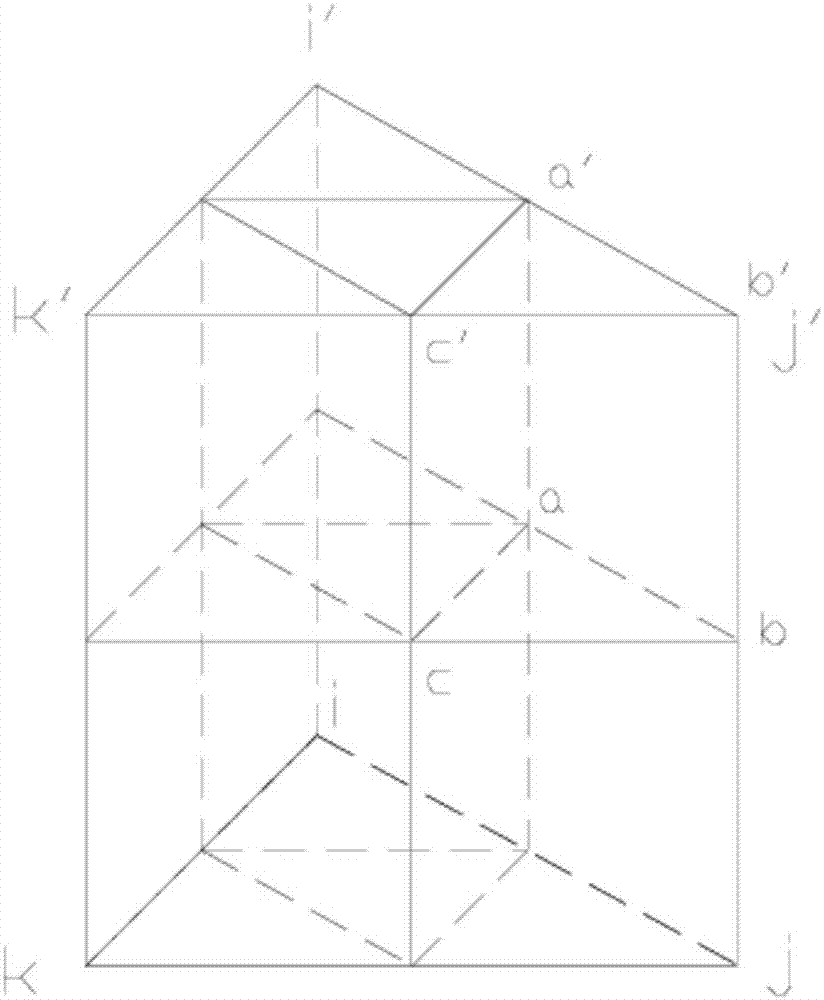
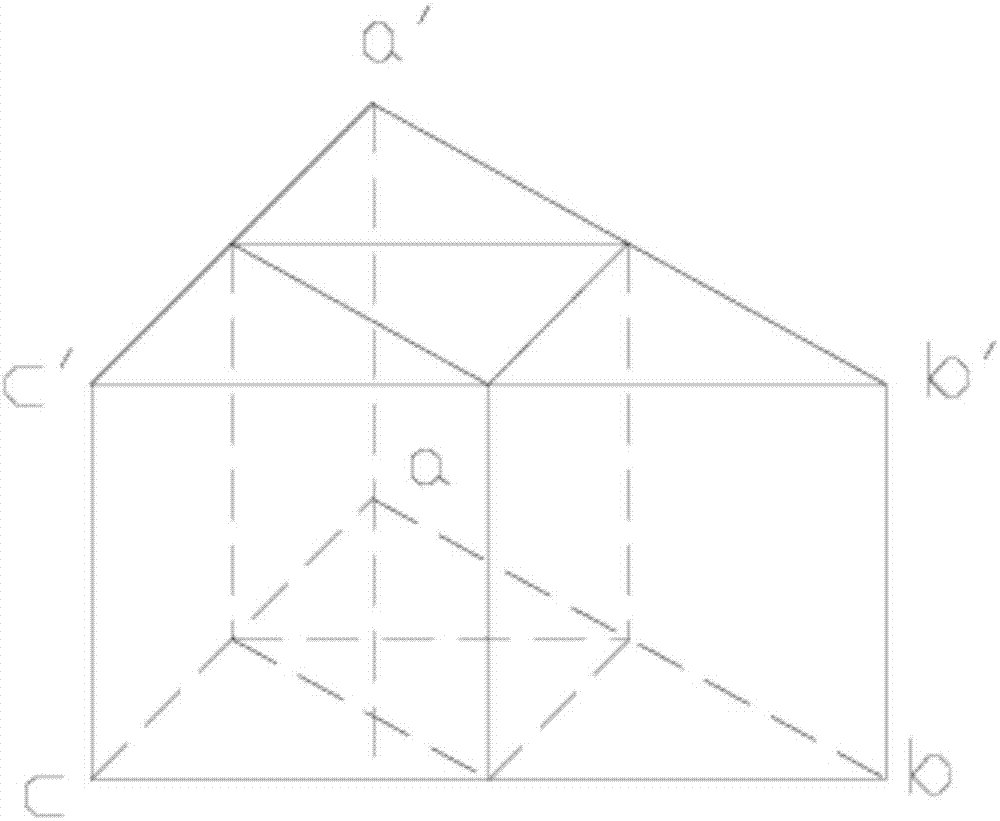
Triple-grid multi-scale finite element method for simulating three-dimensional underground water flow movement

A multi-scale, finite element technology, applied in the field of hydraulics, can solve the problem of low efficiency of three-dimensional multi-scale basis function construction, and achieve the effect of saving calculation consumption, less calculation amount, and ensuring continuity

Active Publication Date: 2017-07-07
NANJING UNIV
View PDF4 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The purpose of the present invention is to provide a triple-grid multi-scale finite element method for simulating three-dimensional groundwater flow movement to solve the problem of low construction efficiency of three-dimensional multi-scale basis functions in the prior art when solving three-dimensional large-scale groundwater problems. The combined area decomposition technology reduces the required calculation consumption by decomposing the structural problem into sub-problems; on this basis, the present invention will also combine Yeh's finite element model to realize the efficient calculation of the three-dimensional continuous Darcy velocity field

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Triple-grid multi-scale finite element method for simulating three-dimensional underground water flow movement
  • Triple-grid multi-scale finite element method for simulating three-dimensional underground water flow movement
  • Triple-grid multi-scale finite element method for simulating three-dimensional underground water flow movement

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0093] Embodiment 1: Three-dimensional continuum steady flow model

[0094] The research area Ω is an area of ​​10km×10km×10m, and the origin is (50m, 50m, 0m) permeability coefficient K x = K y = K z =10 -8 x 2 m / d, the research equation is the steady flow equation:

[0095]

[0096] The boundary conditions and the source-sink term W are determined by the analytical solution H=10 -4 (x 2 +y 2 +z 2 ) is given.

[0097] Sub-example 1.1: Use FEM, MSFEM and ETMSFEM to solve, and divide the study area into the same number of fine units; FEM divides the study area into 120×120×2 grids, and other methods divide the study area into 30 ×30×2 grid; MSFEM divides each coarse unit into a 4×4×1 grid to obtain a fine unit, and ETMSFEM divides each coarse unit into a 2×2×1 grid to obtain a medium unit , and then divide each medium unit into a 2×2×1 grid to obtain fine units.

[0098] figure 2 It is the hydraulic head field of AS, FEM, MSFEM and ETMSFEM on the plane of y=4050...

Embodiment 2

[0108] Example 2: Three-dimensional stochastic logarithmic normal distribution medium steady flow model

[0109] The research area Ω is an area of ​​1km×1km×120m, and the origin is (0m,0m,0m). Permeability coefficient K x =K y =K z = K, where K is a random log-normally distributed coefficient field generated by the sequential Gaussian simulation method in GSLib (Deutsch and Journal, 1998) on a grid of 400×400×8, the variance of lnK is 4, and the correlation The length is 100m. The left and right boundaries of the study area are constant water head boundaries, which are 16m and 11m respectively, and the other boundaries are separated from water, and the source and sink items are 0.

[0110] MSFEM and ETMSFEM are used to solve this example, and the study area is divided into the same number of fine elements. MSFEM and ETMSFEM divide the study area into a 25×25×2 grid. At the same time, we also use two kinds of coarse unit division, 1: MSFEM divides each coarse unit into a ...

Embodiment 3

[0112] Example 3: Unsteady flow model of medium with three-dimensional horizontal gradient and vertical abrupt change

[0113] Consider the following three-dimensional unsteady flow equation:

[0114]

[0115] The research area Ω is an area of ​​10km×10km×120m, the origin is (0m, 0m, 0m), and contains 4 aquifers and 4 aquitards; the permeability coefficient K in the aquifer x =K y =1+x / 50m / d, the permeability coefficient K of the aquitard x =K y =0.005+x / 10000m / d, the vertical permeability coefficient is one-tenth of the horizontal direction; the water storage coefficient is S=5×10 -10 x / m, the left and right boundaries are constant water head boundaries, the water head values ​​are 10m and 1m respectively, the other boundaries are water barrier boundaries, the source and sink items are 0, the time step is 1 day, and the total time is 6 days. The water head changes linearly at the initial moment, which is H 0 = 10-x / 10000m.

[0116] MSFEM and ETMSFEM are used to solve...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

PropertyMeasurementUnit
Coefficientaaaaaaaaaa
Login to View More

Abstract

The invention discloses a triple-grid multi-scale finite element method for simulating three-dimensional underground water flow movement. According to the method, a three-dimensional underground water problem is converted into a variation form, and a boundary condition of the problem is determined; the scales of a thick grid, an intermediate grid and a thin grid are determined; a research region is divided into thick units; each thick unit is divided into intermediate units; each intermediate unit is divided into thin units; an improved three-dimensional linear basis function is constructed; computational consumption needed for constructing a three-dimensional multi-scale basis function is reduced in combination with a domain decomposition method; an effective computing method is adopted to solve simultaneous equations of a water head total stiffness matrix and right-hand sides to obtain water head values; the constructed three-dimensional multi-scale basis function is adopted to replace a finite element basis function in a Yeh finite element model; and Darcy's velocity is solved efficiently. Compared with multiple classic methods, the triple-grid multi-scale finite element method has higher computing efficiency.

Description

technical field [0001] The invention belongs to the technical field of hydraulics, and in particular relates to a triple grid multi-scale finite element method for simulating three-dimensional groundwater flow movement. Background technique [0002] With the rapid development of economy and science and technology, people are paying more and more attention to the numerical simulation of groundwater, and the groundwater problems studied are becoming more and more complex, such as land subsidence, seawater intrusion, and water resource assessment in river basins. Therefore, efficient numerical methods for studying the distribution and movement of groundwater can help us better understand the groundwater system and have important research value. [0003] Because groundwater problems are heterogeneous, and their heterogeneity often spans many scales. If the traditional finite element method is used to directly solve all scales of the medium, fine subdivision is required to ensur...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
CPCG06F30/23
Inventor 谢一凡吴吉春南统超薛禹群纪海峰谢春红
Owner NANJING UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com