Supercharge Your Innovation With Domain-Expert AI Agents!

Outer-level damping method of strap-down inertial navigation system based on adaptive complementation filtering

A technology of complementary filtering and strapdown inertial navigation, applied in the field of navigation strapdown inertial navigation, can solve the problems of sensitive covariance, inability to obtain accurate accelerometer error and gyro drift, and no basis for theoretical derivation, etc., to achieve high stability Effect

Inactive Publication Date: 2018-04-20
HARBIN ENG UNIV
View PDF2 Cites 16 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The traditional external horizontal damping network can well damp the Schuler oscillation error, but it will produce overshoot error when the damping is switched, and the greater the external reference speed error, the greater the overshoot
In addition, its parameters are obtained through a step-by-step trial method, and there is no basis for theoretical derivation
Therefore, the document "Horizontal Damping Algorithm of Strapdown Inertial Navigation System Based on Kalman Filtering Technology" (Chinese Journal of Inertial Technology, 2013, 21(3): 285-288) based on modern control theory, proposes a horizontal damping algorithm based on Kalman filtering technology. algorithm, but the Kalman filter algorithm is very sensitive to the selection of the initial value and the covariance of the process noise. In practical applications, it is impossible to obtain accurate accelerometer error and gyro drift
The document "Design of Horizontal Damping Network of Inertial Navigation System Based on Complementary Filtering" (China Inertial Technology, 2012, 20(2) 157-161) proposed to combine a constant velocity network with excellent high frequency characteristics and a phase lag lead network with low frequency characteristics Complementary filter matching is performed, but when the reference external velocity error measured by Doppler changes with time, the fixed damping parameters cannot achieve a good damping effect, and even cause divergence, which has caused certain limitations

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Outer-level damping method of strap-down inertial navigation system based on adaptive complementation filtering
  • Outer-level damping method of strap-down inertial navigation system based on adaptive complementation filtering
  • Outer-level damping method of strap-down inertial navigation system based on adaptive complementation filtering

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

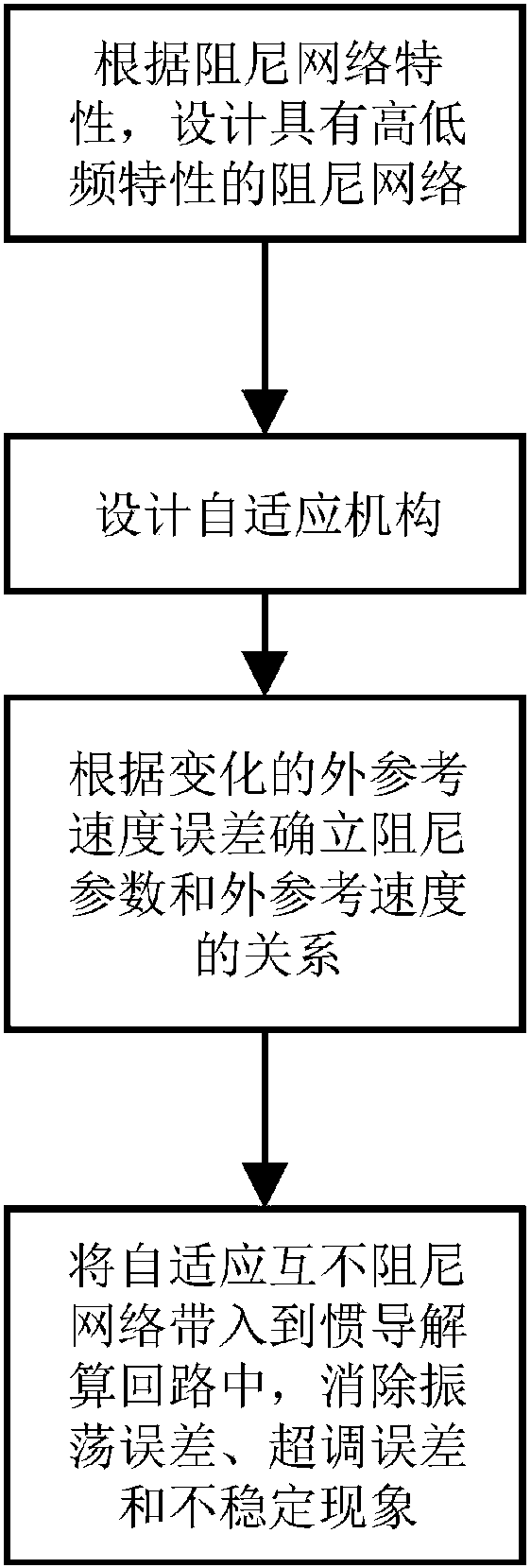
[0043] Embodiment: In the long-term navigation of ships, due to the existence of Schuler oscillation, the undamped inertial navigation system cannot meet the requirements, and the existence of gyro random drift will cause oscillation errors accumulated over time. The traditional external horizontal damping network can Eliminate the oscillatory error, but it will produce overshoot when the damping is switched, and the overshoot is proportional to the difference between the system speed and the external reference speed. The present invention selects the damping according to the external reference speed error that changes with time parameters to achieve higher stability, the implementation process is as attached figure 1 ,Specific steps are as follows:

[0044] Step 1: Analyze the amplitude-frequency characteristics of the constant-velocity network and the phase-lag-lead network, and perform complementary matching of the two networks;

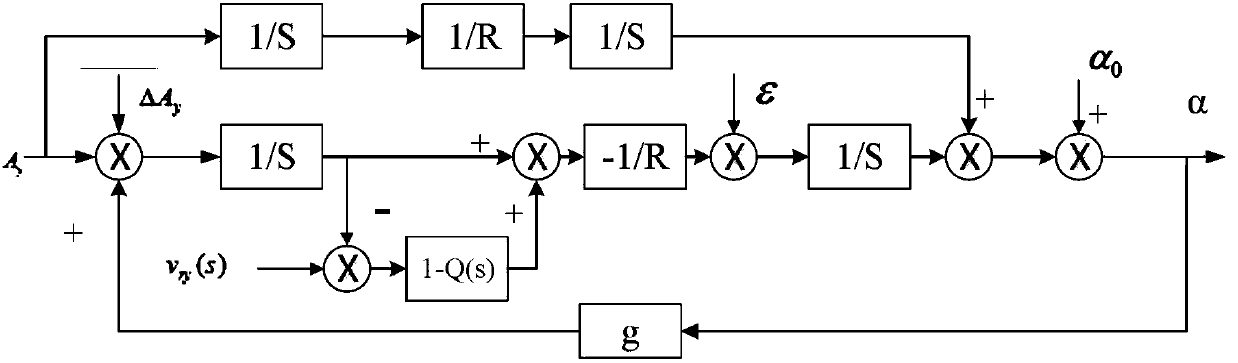
[0045] as attached figure 2 Shown is the...

Embodiment 1

[0088] Embodiment 1: Set at 45.7796°N, 126.6705°E, the carrier running speed is 5m / s, the damping coefficient ξ is substituted into the damping network, η=μ=0.5, and the simulation parameter settings are shown in Table 3.

[0089] Set the external reference speed error according to the following formula, the simulation is as attached Figure 5 Shown:

[0090]

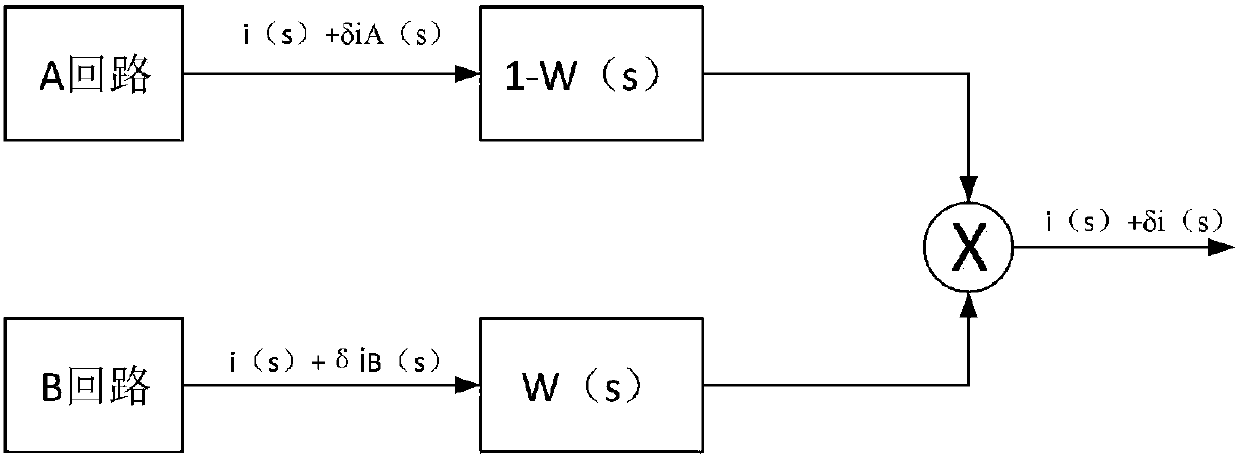
[0091] Since the working mode of the ship is related to the accuracy of the external reference speed, when the external reference speed is inaccurate, only the undamped state is performed. Select the external reference speed error according to the above formula, at t=5h, switch from the non-damping state to the damping state; at t=12h, switch from the damping state back to the non-damping state; Since the speed errors of the inertial navigation system at different time points are different, in order to verify the algorithm, the damping switching process at different time points is realized, and the simulation is car...

Embodiment 2

[0093] In order to verify that the adaptive network based on complementary filtering has engineering applicability, connect PHINS with H / H HZ001 inertial navigation system, use PHINS as a reference, and conduct experiments at a certain location (45.7796°N, 126.6705°E), the initial pitch angle , the roll angle and heading angle are -0.016°, -0.398°, 253.11° respectively, the damping coefficient ξ is substituted, and the Doppler external reference velocity error is as follows:

[0094] δv r =0.5×sin(2πt / 18h)kn

[0095] The constant value drift and noise of the gyroscope and accelerometer are shown in Table 3. The experimental data is analyzed and processed offline, and the state transition is performed at 1 hour to obtain the experimental results. The speed error and attitude angle error are shown in the attached Figure 8 and 9 shown.

[0096] Implementation Effect:

[0097] Embodiment A kind of simulation data verifies the feasibility of the fitting curve, and the speed er...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an outer-level damping method of a strap-down inertial navigation system based on adaptive complementation filtering, which belongs to the technical field of navigation strap-down inertial navigation. In the method, an adaptive complementation filtering technology is employed to reduce an initial error and an oscillation error. During a process of designing damping network,a complementation filtering technology is used to obtain the higher-order damping network; a relation between a damping parameter and an outer reference speed error is searched according to the outerreference speed error changed with time, and an relation expression formula is obtained; the damping parameter is substituted into the damping network, the damping network is introduced to a solutionloop of inertial navigation to obtain a new solution equation. The damping of adaptive complementation filtering damping network eliminates a Schuler oscillation error, an overshoot error due to damping switching and decentralization even divergency phenomenon due to change of the outer reference speed, so that the outer-level damping method has higher stability and practicality.

Description

technical field [0001] The invention belongs to the technical field of navigation strapdown inertial navigation, and in particular relates to an external horizontal damping method of a strapdown inertial navigation system based on adaptive complementary filtering. Background technique [0002] The undamped inertial navigation system is an autonomous navigation system, and the carrier is not disturbed by acceleration, but it contains three kinds of periodic oscillation errors, namely Schuler periodic oscillation, Foucault periodic oscillation and Earth periodic oscillation. For aircraft, missiles and other systems with large acceleration and speed and short service time, the error accumulation is not serious, but for ships with long service time and not too large acceleration, the error is Oscillating, and accumulating over time, the undamped inertial navigation system cannot meet the requirements, and the oscillating error must be damped. The combined navigation system of i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01C21/20
CPCG01C21/203
Inventor 张勇刚卢曼曼李宁李智超
Owner HARBIN ENG UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com