Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Two-dimensional DCT (Discrete Cosine Transform) hardware implementation method and device

A hardware device and a hardware implementation technology are applied in the field of two-dimensional DCT hardware implementation methods and devices, and can solve the problems of inability to increase the main frequency of the system, the bottleneck of the speed of the compression algorithm, and excessive consumption of hardware resources.

Inactive Publication Date: 2018-05-15
VALUEHD CORP
View PDF3 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] In view of this, the embodiment of the present invention provides a two-dimensional DCT hardware implementation method and device to solve the problem that although there are many fast implementation algorithms for two-dimensional DCT in the prior art, they are basically software-based algorithms, and software implementation The two-dimensional DCT module is often the speed bottleneck of the entire compression algorithm
Due to the big difference between hardware implementation and software implementation, the algorithm suitable for software implementation cannot be transplanted to the hardware implementation solution, otherwise it will easily lead to excessive consumption of hardware resources or the failure to increase the main frequency of the system.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Two-dimensional DCT (Discrete Cosine Transform) hardware implementation method and device
  • Two-dimensional DCT (Discrete Cosine Transform) hardware implementation method and device
  • Two-dimensional DCT (Discrete Cosine Transform) hardware implementation method and device

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0059] In the field, a broad sense of DCT includes 8 different types of definitions, among which DCT-II is the most common form. Unless otherwise specified, DCT usually refers to this type, and is generally referred to as Forward DCT. And DCT-III is the inverse conversion formula of DCT-II, generally also called Inverse DCT. The calculation formula of DCT-II is as follows:

[0060]

[0061] Among them, X represents the DCT calculation result, x represents the input data, k=0, 1,..., N-1 and k is an integer, N≥1 and a positive integer.

[0062] In practical applications, a variant formula of the aforementioned DCT-II calculation formula is generally used, which is also called a normalized DCT calculation formula. Specifically, the X in the above DCT-II calculation formula 0 Term multiplied by And multiply the rest by The variant formula is as follows:

[0063]

[0064] among them,

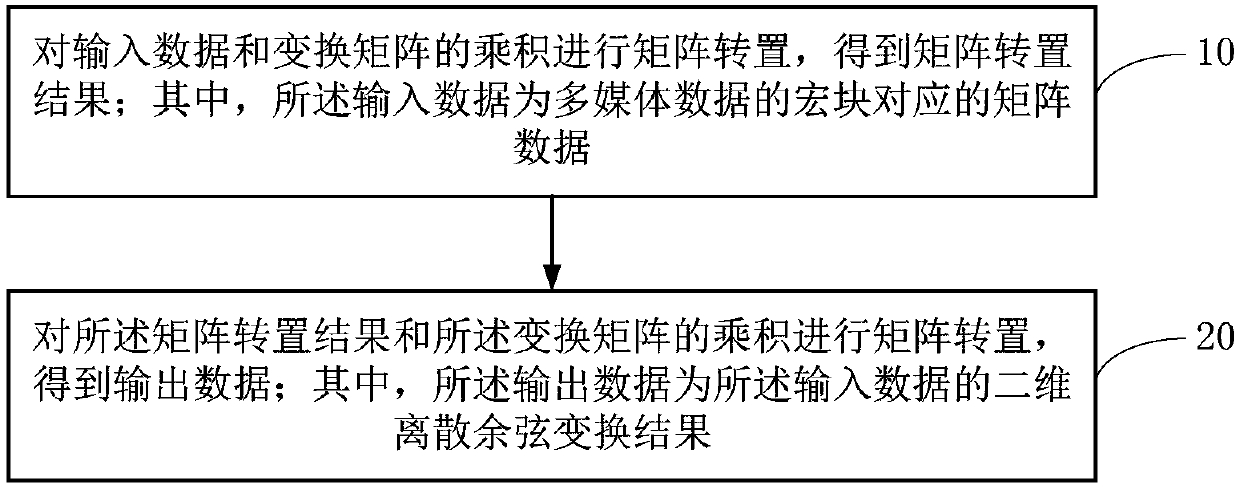
[0065] Since DCT is a separable linear transformation, two-dimensional DCT is equivalent to first p...

Embodiment 2

[0096] In this embodiment, based on the above-mentioned idea of ​​implementing two-dimensional DCT through hardware, the traditional two-dimensional DCT algorithm can be simplified to the calculation of F(X) through hardware;

[0097] Among them, the calculation of F(X) includes two parts, one is to calculate Z=AX, and the other is to matrix transpose the result Z.

[0098] Based on this idea, the discrete cosine transform module, the first discrete cosine transform module, or the second discrete cosine transform module can be further refined into two pieces of hardware to realize the calculation of Z=AX and the matrix transposition of the result Z respectively. .

[0099] The specific structure of the two-dimensional DCT hardware device provided by this embodiment will be described in detail below with reference to the accompanying drawings:

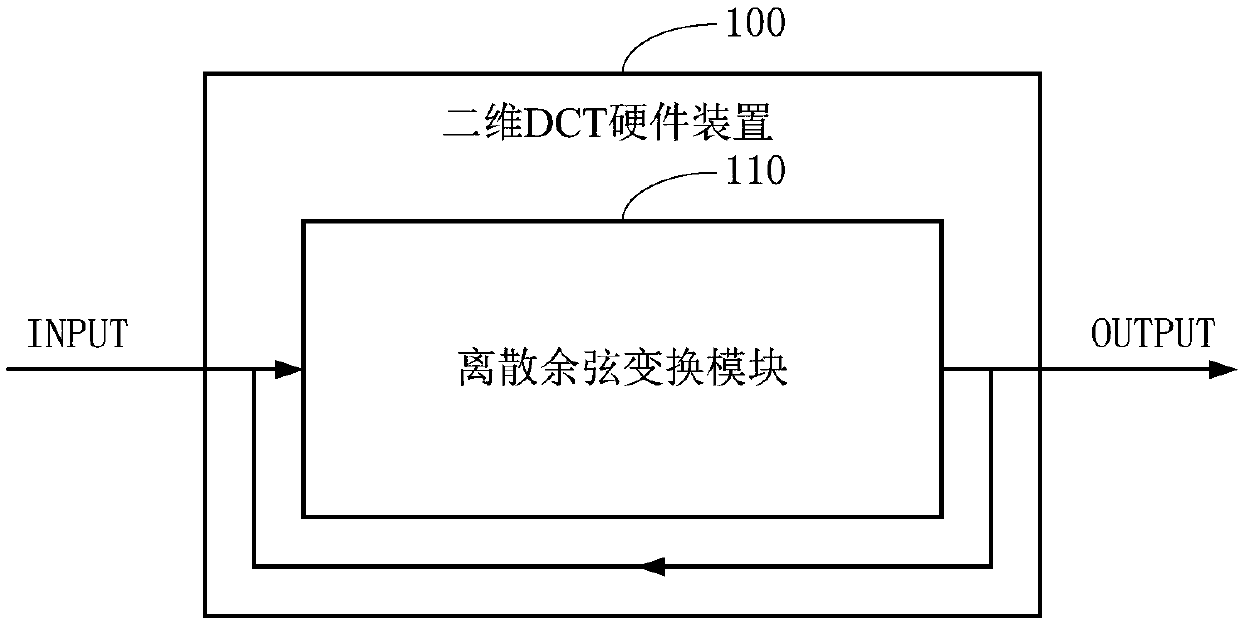
[0100] Such as Figure 4 Shown, based on figure 1 The implementation shown uses a discrete cosine transform module 110, the discrete cosine tr...

Embodiment 3

[0123] For a macro block with a size of 8×8, the calculation formula Z for the product of the input data X and the transformation matrix A n =AX n Expressed as:

[0124]

[0125] Among them, the transformation matrix A is expressed as:

[0126]

[0127] Z n =AX n Represents the product of the input data and the transformation matrix, n=0,1,2,...,7 and is an integer.

[0128] According to the symmetry of the coefficients in the transformation matrix, Z n =AX n The calculation formula is simplified to:

[0129]

[0130]

[0131] The conventional method is to store each coefficient value in the transformation matrix A in the ROM in advance, and then perform multiplication and accumulation according to the rules of matrix multiplication. Because the coefficients in the transformation matrix are all fixed values. therefore, Figure 4 with 5 The DCTImplementation module in can be implemented using distributed algorithms to avoid the use of multipliers.

[0132] Among them, distributed algor...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention is applicable to the technical field of multimedia data compression, and provides a two-dimensional DCT (Discrete Cosine Transform) hardware implementation method and device. The deviceis a two-dimensional DCT hardware device comprising one or two DCT modules; when the two-dimensional DCT hardware device comprises one DCT module, by the DCT module, a product of input data and a transform matrix is subjected to matrix transposition, and then a product of a matrix transposition result and the transform matrix is subjected to matrix transposition so as to obtain a two-dimensional DCT result of the input data; and when the two-dimensional DCT hardware device comprises two DCT modules, by a first DCT module, the product of the input data and the transform matrix is subjected to matrix transposition, and then by a second DCT module, the product of the matrix transposition result and the transform matrix is subjected to matrix transposition so as to obtain the two-dimensional DCT result of the input data. The two-dimensional DCT hardware implementation method and device can implement hardware processing of two-dimensional DCT, is simple in structure and easy to implement and cannot generate negative effects on a main frequency of a system.

Description

Technical field [0001] The invention belongs to the technical field of multimedia data compression, and in particular relates to a two-dimensional DCT hardware realization method and device. Background technique [0002] As we all know, the theoretical feasibility of multimedia data compression technology, especially audio and video data compression technology, lies in the redundancy of the compressed data. Typical redundancy types are: spatial redundancy, time redundancy, symbol redundancy, etc. However, it has been found in practice that it is usually difficult to find the correlation of signals in the time domain, and it is impossible to distinguish redundant information. As a result, people began to turn their attention to the transform domain, such as: K-L (Karhunen-Loeve Transform) transform, Fourier transform, cosine transform and wavelet transform. Under the criterion of selecting the mean square error, K-L transform is the best transform in signal processing methods. ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04N19/42H04N19/126
CPCH04N19/42H04N19/126
Inventor 阮秋文
Owner VALUEHD CORP
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com