A Numerical Calculation Method of Finite Volume Flow Field Based on Non-equidistant Grid
What is Al technical title?
Al technical title is built by PatSnap Al team. It summarizes the technical point description of the patent document.
A finite volume, numerical calculation technology, applied in design optimization/simulation, special data processing applications, etc., can solve problems such as reduced accuracy, unstable format, negative linear weight, etc.
Active Publication Date: 2021-07-27
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF4 Cites 0 Cited by
Summary
Abstract
Description
Claims
Application Information
AI Technical Summary
This helps you quickly interpret patents by identifying the three key elements:
Problems solved by technology
Method used
Benefits of technology
Problems solved by technology
However, once it is extended to non-equidistant grids, its construction is relatively complicated, because its specific expressions are not only related to the physical quantities on the grid points but also related to the grid scale
In addition, whether it is an isometric grid or a non-isometric grid, the linear weight in the above process must be the optimal linear weight to make the overall format achieve the expected design accuracy, otherwise it will reduce the accuracy and even cause negative linear weights to cause the format unstable
Method used
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more
Image
Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
Click on the blue label to locate the original text in one second.
Reading with bidirectional positioning of images and text.
Smart Image
Examples
Experimental program
Comparison scheme
Effect test
Embodiment 1
[0150] Embodiment 1, accuracy test problem. Considering the equation group (1), the initial conditions are: ρ(x,y,0)=1+0.2sin(π(x+y)), u(x,y,0)=0.7, v(x,y, 0)=0.3, p(x,y,0)=1. The exact solution is: ρ(x,y,t)=1+0.2sin(π(x+y-t)), u(x,y,t)=0.7, v(x,y,t)=0.3, p( x,y,t)=1. The calculation end time is t=2. The calculation area is (x,y)∈[0,2]×[0,2]. In order to illustrate that the linear weight in the numerical calculation method of the present invention can be arbitrarily selected, the present invention only takes five groups of numbers with different laws as the linear weight: (1) γ 1 =0.98,γ 2 =0.01,γ 3 =0.01; (2)γ 1 =0.495,γ 2 =0.495,γ 3 =0.01; (3)γ 1 =1 / 3,γ 2 =1 / 3,γ 3 = 1 / 3; (4)γ 1 =0.001,γ 2 =0.001,γ 3 =0.998; (5)γ 1 =0.3,γ 2 =0.4,γ 3 = 0.3.
[0151]
[0152]
[0153] Table 1 Comparison of the numerical accuracy of any five linear weights with the traditional WENO format
Embodiment 2
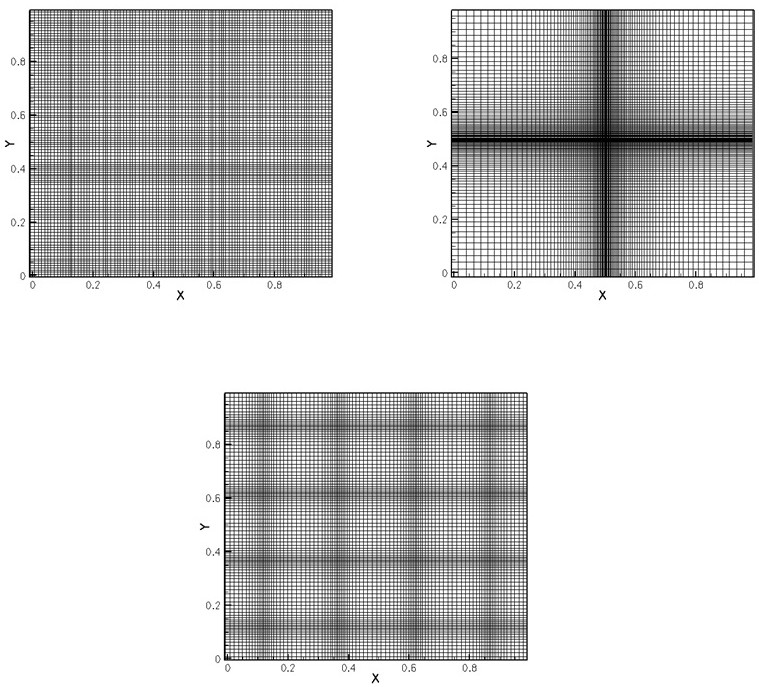
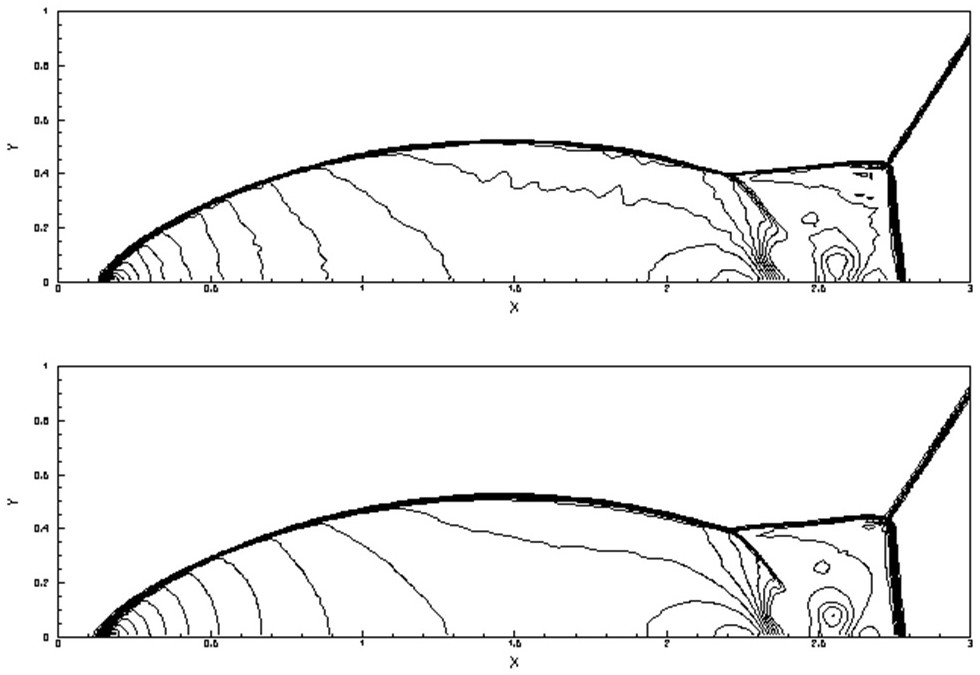
[0154] Embodiment 2, double Mach reflection problem. Such as figure 2 , image 3 As shown, there is a strong shock wave with a Mach number of 10 at 1 / 6 of the left boundary, which is injected at an angle of 60° with the x-axis, and the left and right state values are: (ρ L ,u L ,v L ,E L )=(8,7.145,-4.125,563.544), (ρ R ,u R ,v R ,E R )=(1.4,0,0,2.5). The number of CFL is 0.6, the calculation grid is 300×100, and the end time t=0.2.
Embodiment 3
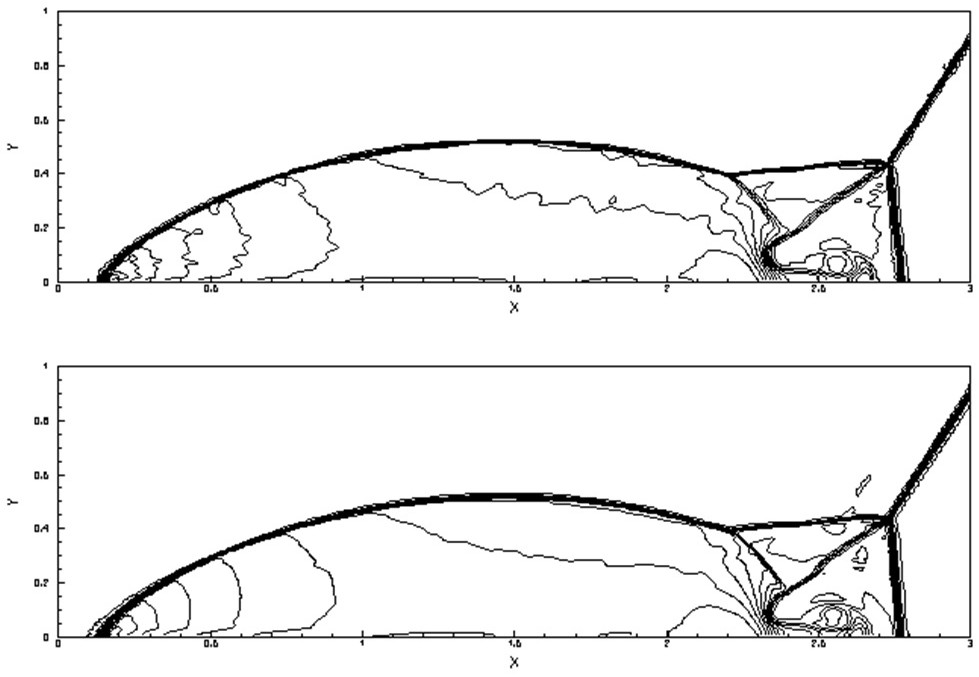
[0155] Embodiment 3, radial symmetric Riemann problem. Such as Figure 4 As shown, considering the fluid dynamics equations (1), the initial conditions are:
[0156]
[0157] The calculation area is [0,1]×[0,1], the number of CFL is 0.6, the calculation grid is 100×100, and the calculation termination time is t=0.13.
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more
PUM
Login to view more
Abstract
A numerical calculation method for finite volume flow field based on non-equidistant grids, which involves a fifth-order finite volume WENO scheme with linear weights. Without reducing the overall numerical accuracy, only three additive A positive number equal to 1 is used as a linear weight, and then subsequent calculations can be performed. Since the numerical format constructed by the present invention does not need to calculate complex linear weights related to the grid scale under non-equidistant grids, it is easier to extend to higher-order WENO schemes, moving grids, or flow fields in adaptive grids calculate. In addition, the present invention, like the traditional WENO format, uses the Runge-Kutta time-discrete method with good stability, simple operation and easy programming to solve the problem. Finally, the present invention verifies its superiority in flow field calculation by comparing it with the traditional formula through specific numerical examples.
Description
technical field [0001] The invention discloses a finite volume flow field numerical calculation method based on non-equidistant grids, which can be used in computational mathematics, aerodynamics, magnetohydrodynamics, aerospace, missile launching, automobile industry, civil engineering, environmental engineering, ships , meteorological engineering and other technical fields. Background technique [0002] In recent decades, the high-order numerical solution format of hyperbolic conservation law equations has been the key research content, and its application fields include computational fluid dynamics, computational astronomy, semiconductor simulation, traffic flow models, and magnetohydrodynamics. The main difficulty in solving the equations of these problems lies in the complexity of the solution. Even if the initial value is smooth, it will evolve over a period of time to produce complex solution structures such as shock waves, contact gaps, and sparse waves. In addition...
Claims
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more
Application Information
Patent Timeline
Application Date:The date an application was filed.
Publication Date:The date a patent or application was officially published.
First Publication Date:The earliest publication date of a patent with the same application number.
Issue Date:Publication date of the patent grant document.
PCT Entry Date:The Entry date of PCT National Phase.
Estimated Expiry Date:The statutory expiry date of a patent right according to the Patent Law, and it is the longest term of protection that the patent right can achieve without the termination of the patent right due to other reasons(Term extension factor has been taken into account ).
Invalid Date:Actual expiry date is based on effective date or publication date of legal transaction data of invalid patent.
Login to view more 
Login to view more