Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Fractional order hidden chaotic system with linear balance point

A fractional-order system, chaotic system technology, applied in digital transmission systems, transmission systems, secure communication through chaotic signals, etc., can solve the optimization without considering time, ignoring time finiteness, only emphasizing system robustness and other problems, Achieve the effect of limited time synchronization and rich diversity

Active Publication Date: 2019-10-11
QILU UNIV OF TECH +1
View PDF7 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Another important issue is that many synchronization methods only emphasize the robustness of the system without considering the optimization of time, ignoring the limited time

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fractional order hidden chaotic system with linear balance point
  • Fractional order hidden chaotic system with linear balance point
  • Fractional order hidden chaotic system with linear balance point

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0044] The fractional-order hidden chaotic system with a linear equilibrium point involved in this embodiment specifically includes the following steps:

[0045] Step 1: First give the definition of the Caputo fractional derivative:

[0046]

[0047] Where q is the order of the differential operator, t and A are limits, w is the smallest positive integer, w-1<q<w. Γ(*) is a gamma function, and f(*) is a continuous function.

[0048] The relevant properties of Caputo fractional differential are as follows:

[0049] Property 1: We consider general fractional differential equations

[0050]

[0051] The general solution of the equation is

[0052] x(t)=x(0)E q (At q ), (3)

[0053] and the Mittag-Leffter function is

[0054]

[0055] Then according to the finite-time stability theory of fractional order systems, the following Lemma 1 and Lemma 2 are introduced.

[0056] Lemma 1: For a general fractional order system, if it satisfies

[0057]

[0058] where x=...

Embodiment 2

[0070] The fractional-order hidden chaotic system with linear equilibrium points involved in this embodiment, based on the finite-time stability theory of fractional-order systems, designs a finite-time synchronous controller and a combined synchronous controller for fractional-order systems with hidden attractors.

[0071] Finite-time synchronization: Assuming the driving system is formula (8), the response system is as follows:

[0072]

[0073] Wherein, m=0, n=0. let e 1 =x 1 -x,e 2 ==y 1 -y,e 3 =z 1 -z,q=0.99, the error system is

[0074]

[0075] Then we get the following theorem.

[0076] Theorem 1: For the error system (11), we design the finite-time synchronous controller as

[0077]

[0078] Among them, k 1 and B 1 is the scaling parameter, the error system (11) in finite time t 1 converges to zero, and

[0079]

[0080] Proof: From Lemma 1, we get

[0081]

[0082] According to formula (7), we get

[0083]

[0084] Therefore, we come t...

Embodiment 3

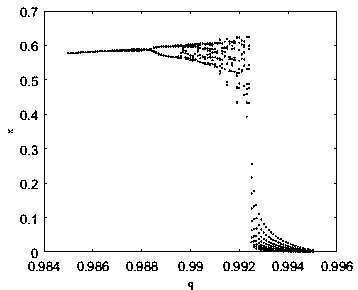
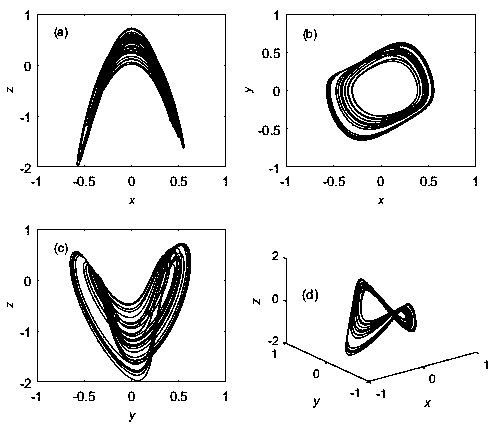
[0120] In the simulation, in order to observe the chaos synchronization between different initial values ​​of the fractional order chaotic system, the finite time synchronization and combined synchronization are studied by using the predictive correction method. For finite-time synchronization, the total number of iterations is 600, and the order of all fractional-order systems is q = 0.99. The initial value for finite-time synchronization is [x(0) y(0) z(0) x 1 (0)y 1 (0)z 1 (0)]=[0.1 0.5 0.5 0.2 0.6 0.4], according to formula (5), get

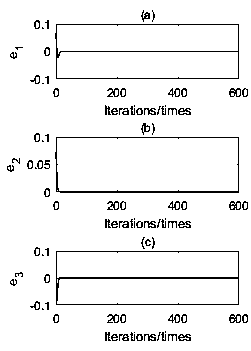
[0121] Such as Figure 3-4 , limiting the total number of iterations to 600 for clean results, e 1 ,e 2 ,e 3 converges approximately to zero at the 12th iteration, while x-x 1 ,y-y 1 ,z-z 1 Simultaneously achieve synchronization. The results show that the errors between the drive system and the response system converge to zero without considering the calculation error, and the error system is gradually stable within a finite time....

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the technical field of automatic control methods, and particularly relates to a fractional order hidden chaotic system with a linear balance point. A new fractional order chaotic system is provided. A fractional order chaotic system with hidden chaotic attractors is generated, and a finite time synchronization method and a combined synchronization method of the chaotic system are designed. The system enriches the diversity of the fractional order chaotic system with hidden attractors. According to the finite time stability theory, finite time synchronization of the fractional order chaotic system with the hidden attractors is achieved. A reference is provided for finite time stability of other fractional order chaotic systems. A combined synchronization method of the fractional order chaotic system is provided, and due to the natural advantages of combined synchronization in information transmission application and the complexity of the fractional order system,the fractional order chaotic system has higher security than many other types of synchronization and integer order chaotic systems in the aspect of realizing secure communication.

Description

technical field [0001] The invention belongs to the technical field of automatic control methods, and in particular relates to a fractional-order hidden chaotic system with linear equilibrium points. The designed fractional-order chaotic system has countless equilibrium points and is linear. Background technique [0002] With the development of computer technology, the discovery of new chaotic systems has aroused great interest of many researchers. In 1994, the hidden chaotic system was proposed for the first time. Hidden attractors exist in many natural phenomena and some important fields, such as the famous nasal Hoover oscillator, drilling system, aircraft control, convective fluid motion, etc., security communication, etc. In addition, hidden chaotic attractors also have some disadvantages, which may lead to unexpected and catastrophic results. The hidden chaotic system can be divided into the following categories: the attractor of the chaotic system is a surface equili...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/00
CPCH04L9/001H04L2209/12
Inventor 张芳芳刘加勋舒明雷黄明明孙凯马凤英
Owner QILU UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com