Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for predicting pneumatic hammer of pipeline

A pipeline gas and pipeline technology, applied in the field of gridless particles based on the natural gas pipeline transmission problem, can solve the problems of reducing calculation accuracy, affecting the efficiency and stability of calculation, and achieve the effect of convenient impact problems

Pending Publication Date: 2020-01-17
TIANJIN UNIV
View PDF0 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In order to reduce the calculation error caused by the gas-state vertical interface assumption, an improved interface tracking technique is proposed by assuming that the gas state changes linearly within a single grid distance, but this affects the efficiency and stability of the calculation, and may also be caused by interpolation errors Accumulation of the accumulation reduces the calculation accuracy, in view of the above problems, the present invention proposes a meshless particle method based on the Lagrang particle model

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for predicting pneumatic hammer of pipeline
  • Method for predicting pneumatic hammer of pipeline
  • Method for predicting pneumatic hammer of pipeline

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

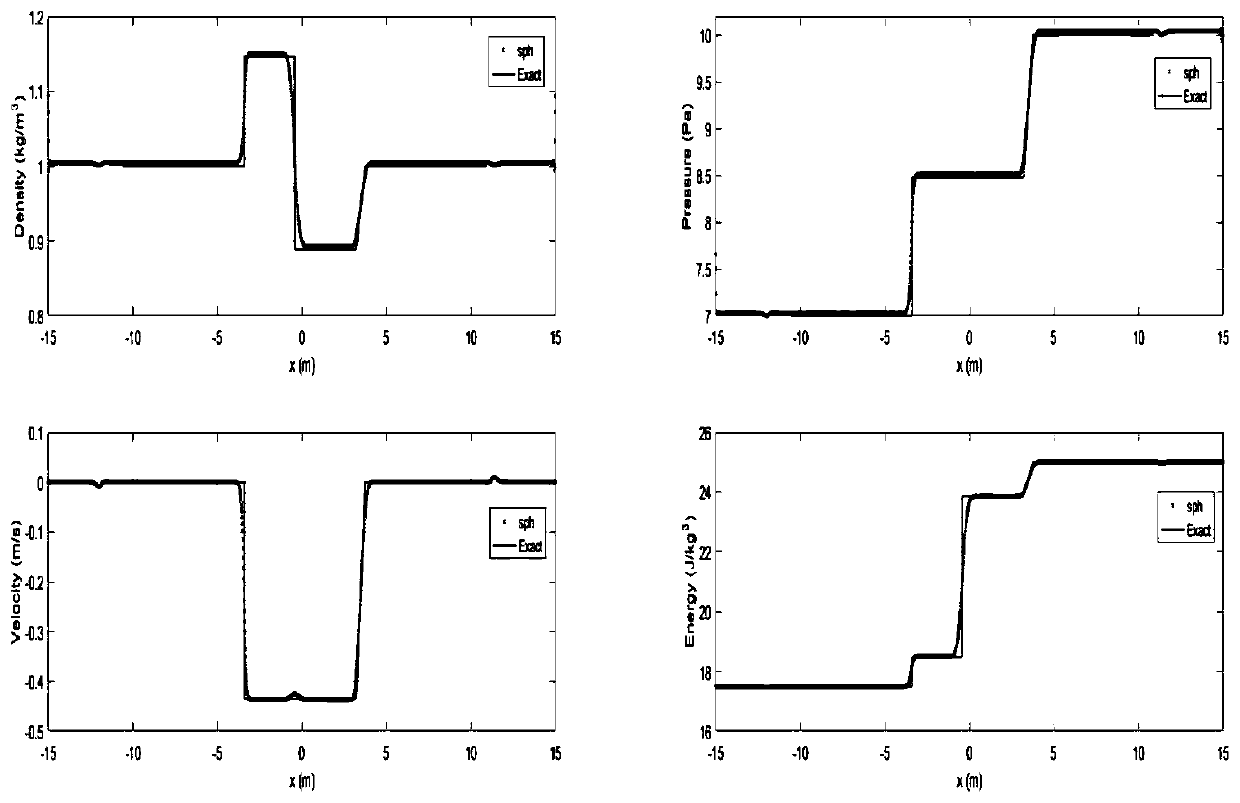
[0063] The technical problem solved by the present invention is to provide a Lagrangian particle method for solving the problem of natural gas pipeline transmission. The method adopts the method of smooth particle hydrodynamics to solve the physical equation of the shock tube under the moving coordinate system, and fully considers the strong stability of the gas. The influence of compressibility can more conveniently simulate the impact of gas on the pipeline under the premise of satisfying the numerical accuracy.

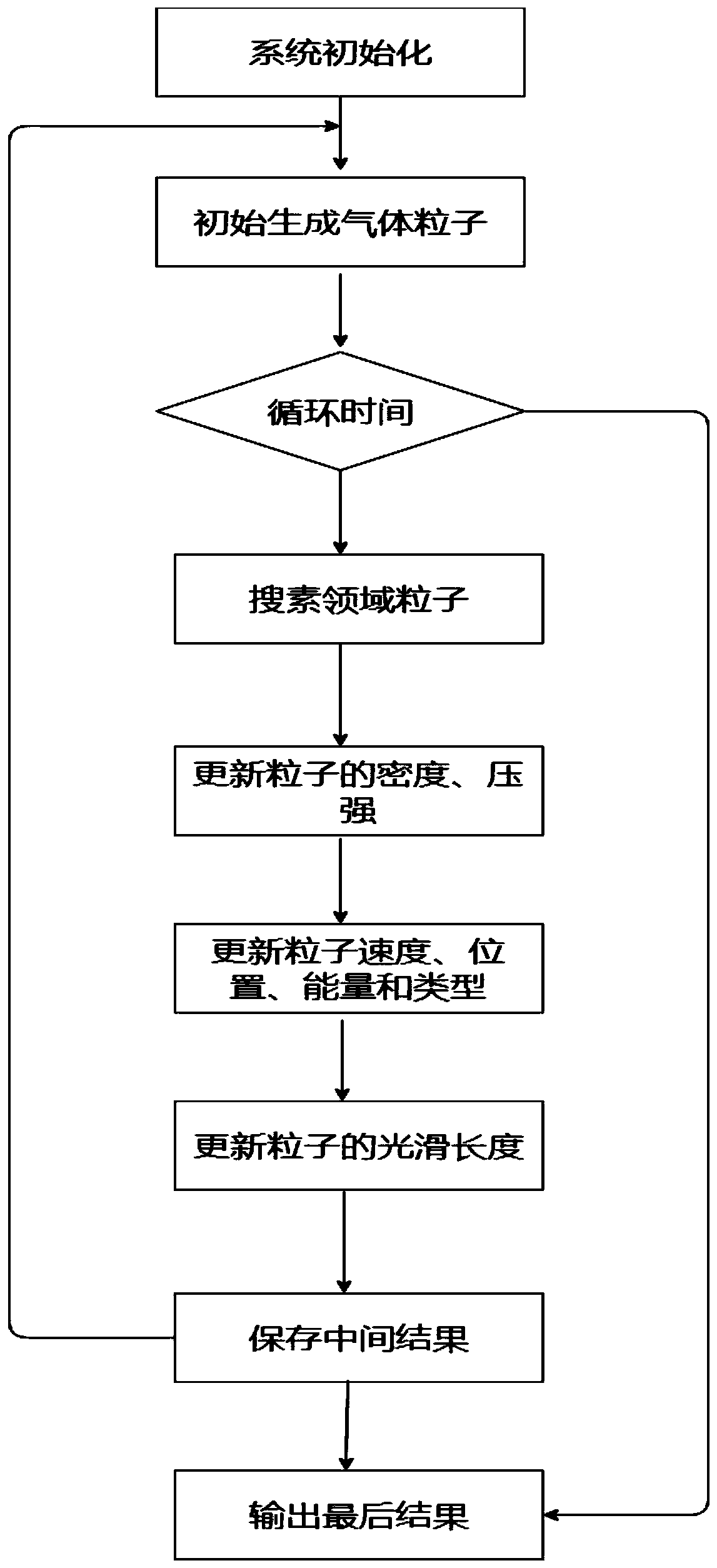
[0064] Step 1, initialization: related variables and particle information of the initialization system;

[0065] Step 2, generating particle information;

[0066] Step 3, list the solution equations and iteratively calculate:

[0067] According to the principle of the natural gas pipeline problem, the mathematical model of the physical model can be obtained, that is, the governing equation in the Lagrangian form is:

[0068]

[0069]

[0070]

[0071] wh...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to the technical field of fluid mechanics, and provides a method for solving a natural gas pipeline transmission problem. Therefore, the technical scheme adopted by the inventionis as follows: the method for predicting the pneumatic hammer of the pipeline considers the influence caused by strong compressibility of gas, solves a shock tube physical equation under a moving coordinate system by adopting a smooth particle hydrodynamic method, and simulates the impact of the gas on the pipeline. The method is mainly applied to design and manufacturing occasions such as natural gas pipelines.

Description

technical field [0001] The invention relates to the technical field of fluid mechanics, in particular to a gridless particle method based on the natural gas pipeline transmission problem. Background technique [0002] For the transportation of gas in natural gas pipelines, due to the strong compressibility of gas, the calculation and simulation of gas are obviously different from other fluids. For this problem, the commonly used methods mainly include interface tracking technology based on the characteristic line method and finite volume methods, etc. In order to reduce the calculation error caused by the gas-state vertical interface assumption, an improved interface tracking technique is proposed by assuming that the gas state changes linearly within a single grid distance, but this affects the efficiency and stability of the calculation, and may also be caused by interpolation errors Accumulation reduces the calculation accuracy. To solve the above problems, the present i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/28G06F111/10
Inventor 侯庆志李俊练继建魏建国党建武
Owner TIANJIN UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com