Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Multi-mobile-robot formation method based on distributed preset time state observer

A technology of mobile robots and state observers, which is applied in the direction of instruments, motor vehicles, non-electric variable control, etc., can solve the problems of not being able to complete task requirements well, and achieve the effects of improving effects, high precision, and ensuring accuracy

Active Publication Date: 2020-05-29
NANJING UNIV OF POSTS & TELECOMM
View PDF5 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0002] A single mobile robot has limited capabilities in information acquisition, processing, and autonomous control and planning, making it unable to fulfill task requirements well in some large and complex task environments and spaces.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Multi-mobile-robot formation method based on distributed preset time state observer
  • Multi-mobile-robot formation method based on distributed preset time state observer
  • Multi-mobile-robot formation method based on distributed preset time state observer

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0045] In order to better understand the content of the patent of the present invention, the technical solution of the present invention will be further described below in conjunction with the drawings and specific embodiments.

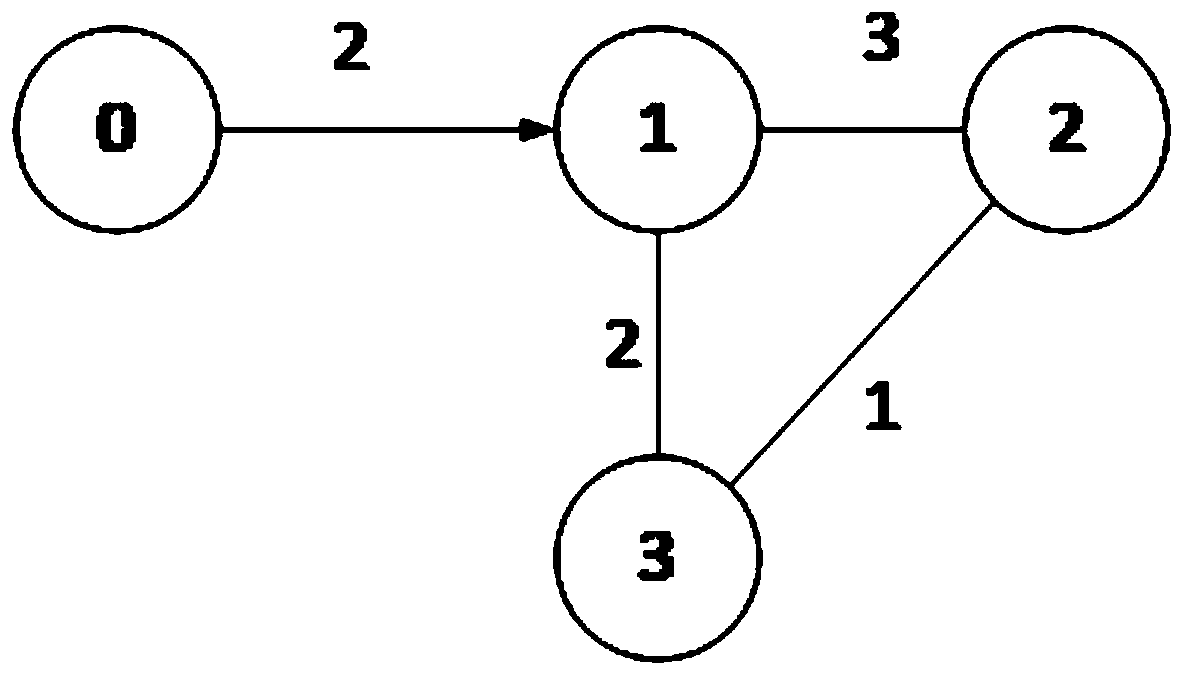
[0046] Such as Figure 1-6 As shown, the multi-mobile robot formation method based on the distributed preset time observer includes the following steps:

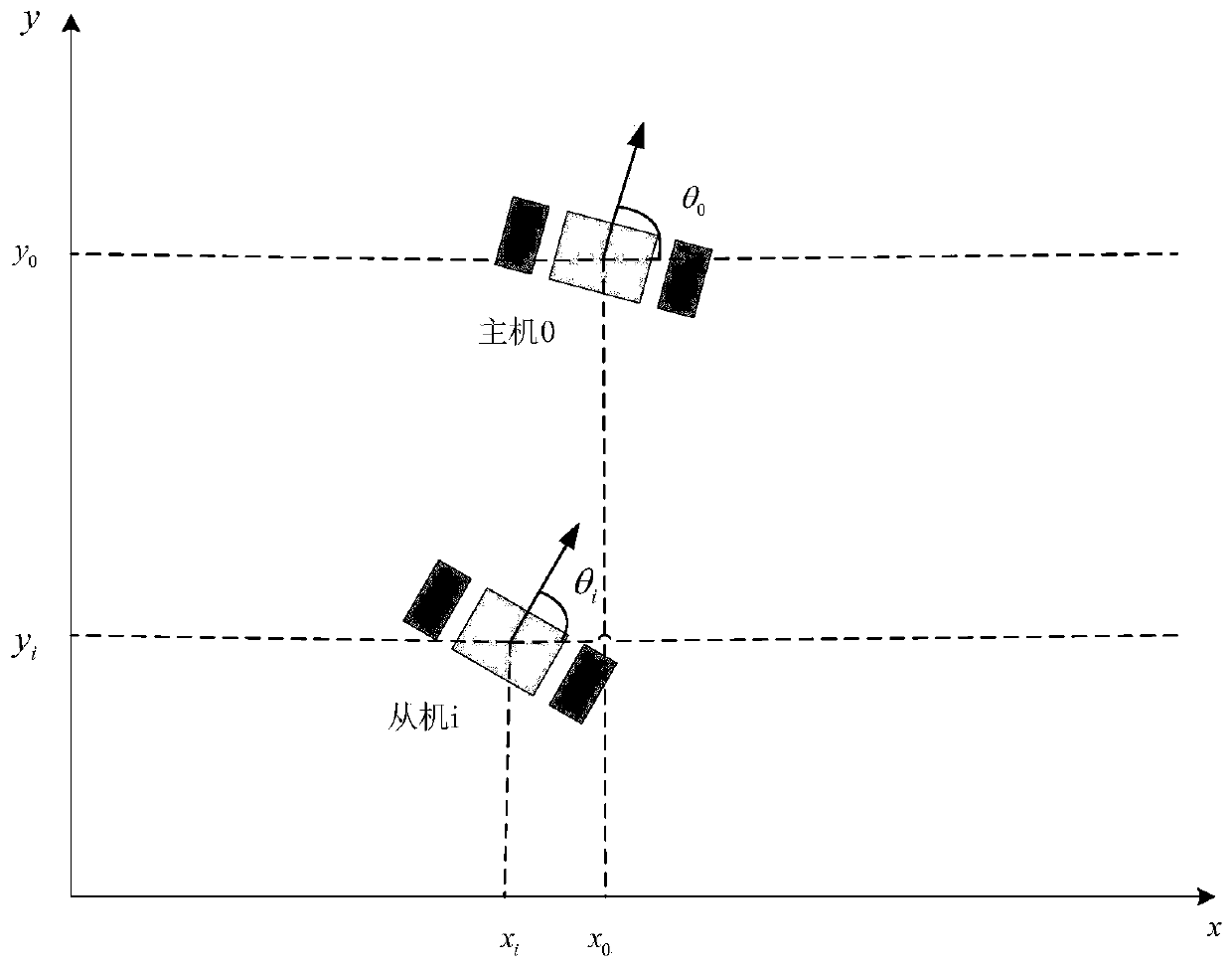
[0047] Step 1: Kinematics modeling: According to the operational characteristics of the multi-mobile robot, the kinematic equations of the multi-mobile robot are established, where the kinematic model of the multi-mobile robot is as follows figure 2 shown. The mobile robot is selected as a wheeled robot under the two-dimensional plane of the global coordinate system, and its kinematic equations can be described as follows:

[0048]

[0049] Among them, i is the number of mobile robot; N is a normal number, indicating the number of multiple mobile robots; Δ={1,2,...,N} is the number set of mult...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a multi-mobile-robot formation method based on a distributed preset time state observer. The invention belongs to the technical field of multi-mobile-robot cooperative control.The invention discloses the multi-mobile-robot formation method based on the distributed preset time state observer, the distributed preset time observer can directly observe the real formation errorvalue of a slave mobile robot and the position, angle and angular velocity of a host, the convergence time of the observer can be set offline in advance, and the accuracy, flexibility and safety of the observation effect can be guaranteed; a mobile robot formation controller provided by the invention also uses a preset time algorithm such that the time for completing the formation of a formationcan be ensured to be preset offline; meanwhile, a GPS positioning system, a laser radar and an inertia measurement unit (including an accelerometer, a gyroscope and a magnetometer) are used for obtaining the relative position and angle between the mobile robots, high precision can be guaranteed, it is guaranteed that the observation value of the observer is closer to the actual value, and the effect of multi-mobile-robot formation is improved.

Description

technical field [0001] The invention belongs to the technical field of collaborative control of multiple mobile robots, and in particular relates to a multi-mobile robot formation method based on a distributed preset time state observer. Background technique [0002] Single mobile robots have limited capabilities in information acquisition, processing, and autonomous control and planning, which makes them unable to fulfill task requirements well in some large and complex task environments and spaces. A multi-mobile robot system is a collection of multiple mobile robots with independent and autonomous capabilities. They are a whole, forming a robot formation, coordinating with each other and avoiding conflicts. [0003] The multi-mobile robot system has the characteristics of distribution in terms of space, time, information, resources, and functions. In addition to the above aspects of time and space, it also has the characteristics of complementarity and redundancy, which s...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05D1/02
CPCG05D1/0257G05D1/0223G05D1/0214G05D1/0221G05D1/0278G05D1/0276
Inventor 葛晟宇蒋国平周映江刘尚
Owner NANJING UNIV OF POSTS & TELECOMM
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com